It is the most fundamental task to track the hidden state of a dynamical system by using the noisy measurements in real-time in many fileds, including singal processing (Yadav et al., 2023), navigation (Hu et al., 2003), information fusion (Xu et al., 2004), and automation control (Menner et al., 2023; Mercorelli, 2012a). A large number of algorithms were proposed to stress this issue, such as Bayesian estimation (Coué et al., 2003) and particle filter (Hue et al., 2002).

Kalman Filter (KF) (Kalman, 1960) is also an efficient recursive filter that can track the state of dynamic systems from a series of incomplete measurements with additive white Gaussian noise (AWGN). Low complexity implementation of KF, combined with theoretical foundation, resulted in it quickly becoming the popular method for state estimation problems.

The original Kalman Filters perform well in linear and Gaussian systems. The reality is that many nonlinear phenomena are encountered in real-world multi-sensor systems. Therefore, several variants of Kalman Filters are available to meet the requirements of nonlinear dynamic systems, including Extended Kalman Filters (Maybeck, 1982) (EKF) and Unscented Kalman Filters (UKF) (Wan and Van Der Merwe, 2001).

There are still limitations associated with the application of EKF and UKF in practical applications. Specifically, the Kalman Filter is a model-based method, and the performance of state estimation heavily depends on model accuracy. Furthermore, the noise covariance matrix is determined by prior process noise and measurement noise, which are assumed to be Additive White Gaussian Noise (AWGN). Additionally, there is no guarantee that the AWGN will accurately reflect the actual performance of the information fusion.

Several variants of Kalman Filters were proposed to overcome the above issue. For example, Huang et al. (2020) introduced a sliding window variational adaptive Kalman filter to simultaneously modify the state estimation and covariance matrix. Yu and Li (2021) presented an adaptive Kalman Filter that concentrated on unknown covariances of both dynamic multiplicative noise and additive noises. Xiong et al. (2020) employed a parallel adaptive Kalman Filter to estimate the attitude of the vehicle based on the Inertial Measurement Unit (IMU). Paolo Mercorelli introduced (Mercorelli, 2012b) a combination of the augmented EKF and EKF for sensorless Valve Control which avoids complicated observation.

Recent years have seen the application of deep learning techniques to multiple real-world applications such as computer vision (Voulodimos et al., 2018) and natural language processing (Otter et al., 2020). Particularly, some Deep Neural Networks (DNNs), such as the Recurrent Neural Network (RNN) (Elman, 1990), Long Short-Term Memory Network (LSTM) (Hochreiter and Schmidhuber, 1997), Gated Recurrent Unit (GRU) (Chung et al., 2014), and Transformer (Vaswani et al., 2017), have demonstrated excellent performance when it comes to processing time series data. For example, Xia et al. (2021) presented staked GRU and RNN to predict the payload of electricity. Zhang et al. (2020) applied LSTM to estimate the battery's state of health.

Furthermore, deep learning techniques have been utilized by some researchers to enhance the effects of the Kalman Filters. For example, Rangapuram et al. (2018) introduced RNN to forecast the state space parameters of linear systems. Coskun et al. (2017) utilized LSTM to learn the noisy parameters and motion model of the Kalman filters. EKFNet (Xu and Niu, 2021) used BPTT (Ruder, 2016) to learn the process and measurement noise from the measurement. Bence Zsombor Hadlaczky applied neural networks and EKF to estimate the wing shape (Hadlaczky et al., 2023). Dahal et al. (2024) introduced RobustStateNet, which applied RNN and Kalman Filters to perform ego vehicle state estimation. Zhang et al. (2023) adopted the Transformer to pre-estimate the vehicle mass, thus acting as an observation for EKF. Luttmann and Mercorelli (2021) employed EKF to accelerate the convergence of the learning system.

In this work, we present KalmanFormer, a hybrid data-driven and model state estimator that can be used to perform information fusion in multi-sensor systems. Our KalmanFormer uses a Transformer framework to track the Kalman Gain instead of computing it from the statistic moments.

The structure of this paper is organized as follows: Section 2 introduces the Kalman Filters and Transformer architecture. Section 3 details the methodology of the proposed KalmanFormer. Experiments will be discussed in Section 4. Section 5 concludes the whole paper.

The Kalman Filter algorithm (KF) is a classic algorithm of information fusion technology and is widely used to solve various optimal estimation problems. The classic Kalman Filters are composed of a state transition model and an observation model, which are expressed as follows:

1N, where Zi=[z1(i),z2(i)...,zT(i)],Xi=[x0(i),x1(i)...,xT(i)]    (15)

The empirical loss function for the i-th trajectory training inside the dataset is defined as follows:

li(Θ)=1Ti∑k=1Ti||ΨΘ(x^k-1i,zk(i))-xk(i)||2+ξ·||Θ||2    (16)

where ΨΘ represents the output of our KalmanFormer, Θ is the trainable parameters inside the KalmanFormer, and ξ is regularization coefficient. Let Δxk(k)=xk(k)-x^k|k-1(k) and Δzk(k)=zk(k)-ẑk|k-1(k) be the state prediction error and the measurement innovation at timestamp k. The partial derivative of the loss function respective to the Kalman gain matrix is:

∂l(Θ)∂Kk(Θ)=1LTk∑k=1L∑k=1Tk∂||Δxk(k)-Kk(Θ)Δzk(k)||22∂Kk(Θ)    (17)

By plugging into the chain rule:

∂l(Θ)∂(Θ)=∂l(Θ)∂Kk(Θ)∂Kk(Θ)∂(Θ)    (18)

We can adopt a stochastic gradient descent algorithm to optimize Θ by using ∂l(Θ*)∂(Θ*)=0.

4 Numerical experiments

In this section, we design a series of experiments to evaluate the performance of our proposed KalmanFormer and compare it to some other benchmarks. As a first step, we make a brief description of the training setup of our KalmanFormer. Following that, we conduct the simulation experiments including nonlinear cases to evaluate the performance of our proposed method. At the end of this section, IMU and GPS information are employed to investigate the effectiveness of our proposed method.

4.1 Implement details

To be specific, the dimensions of concatenated observation difference and innovation difference are 8, which is the input to the encoder for the transformer. Also, the dimensions of state evolution difference and state update difference are 4, which is the input to the decoders of Transformer. The feed-forward dimension inside the encoder and decoder is 64, and 2 heads are employed in the multi-head attention mechanism. Furthermore, we stack the encoder and decoder 2 times to produce the output. After the output is obtained, a fully connected layer is used to generate the learned Kalman Gain.

Furthermore, we conduct all of our training and validation experiments on the Pytorch (Paszke et al., 2019) platform using a single RTX 3090 GPU card, CUDA11.6, and cuDNN version 8. Furthermore, the Cosine Annealing Schedule is employed to adjust the learning rate in the training procedure, which can be expressed as follows:

ηt=ηmin+12(ηmax-ηmin)(1+cos(TcurTmaxπ))    (19)

where ηt represents the learning rate of the current iteration, ηmin and ηmax mean the predefined minimum and maximum learning rate respectively. Tcur and Tmax are the current iteration and maximum iterations respectively.

Adam (Kingma and Ba, 2014) optimizer is used to train the KalmanFormer. Different hyper parameters are performed on the simulation and multi-sensor fusion experiments. The specific information about the hyperparameters is shown in Table 1.

Table 1. Details information about the hyperparameters.

4.2 Simulation experiments

In this section, a series of simulation experiments are designed to demonstrate the effort of our proposed KalmanFormer. We make a comparison with EKF and KalmanNet (Revach et al., 2021).

4.2.1 Test metric

Mean Square Error (MSE) is used to evaluate the effect of our proposed KalmanFormer, which is computed as follows:

MSE=1N∑j=1N∑i=1T|(xest-xtrue)i|2    (20)

where xest means the output from our KalmanFormer, xtrue represents corresponding ground-truth. N means the number of the testing trajectories. T is the length of current trajectory.

4.2.2 Non-linear Lorenz attractors

The Lorenz attractor (Tucker, 1999) describes a non-linear chaotic system used for atmospheric convection. The Lorenz system is expressed by following three differential equations that define the convection rate, the horizontal temperature variation, and the vertical temperature variation of a fluid:

∂z1∂t=10(z2-z1),∂z2∂t=z1(28-z3)-z2,∂z3∂t=z1z2-83z3,    (21)

In order to generate the simulated trajectories, we run the Lorenz equations described at Equation 21 with a time step of Δt = 0.05 and add Gaussian noise of standard deviation σ = 0.05 to the results. The noisy data is considered as the measurements while the decimated data is regarded as the ground truth trajectory for our experiments. The trajectories of ground truth and noisy observations are shown in Figure 6.

Figure 6. Illustration of trajectories.

Assuming a three-dimensional vector x=[z1,z2,z3]T∈R, the dynamic matrix A(x) of the system from Equation 21 is expressed as follows:

A(x)=[-1010028-z3-10z20-83][z1z2z3]    (22)

After that, Taylor expansion is used to obtain the state transition function:

Fk(xk)=I+∑j=1J(A(xk)k)jj!    (23)

where I represents the identity matrix and J means the number of Taylor expansion. We set J = 5 in our experiments. For the measurement model, we set H = I. For the noise parameters, we set Q = q2I, R = r2I, where q=0.8, r=1.

4.3 Multi-sensor information fusion

We further evaluate the effectiveness of the proposed KalmanFormer in multi-sensor fusion. We employ the Michigan NCLT dataset (Carlevaris-Bianco et al., 2016) with different types of sensors to perform our experiments.

The NCLT dataset was obtained from a mobile robot platform equipped with various sensors, including Real Time Kinematic GPS, IMU, Consumer-grade GPS, etc. In our experiments, IMU is employed to provide angular speed information and acceleration information, which is used to design the state transition function. The consumer-grade GPS is applied to provide the observation of the displacement. The Real-Time Kinematic GPS is used to generate a more accurate state of the system, which is used to evaluate the effectiveness of the proposed method.

4.3.1 Coordinates definition

A North-East-Down (NED) frame is employed to describe the robot's pose and position. Furthermore, the fixed origin point of the NED frame is shown in Table 2.

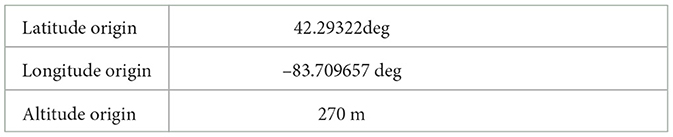
Table 2. Origin point information for NED frame.

The angular and acceleration information from the IMU is measured in the IMU's reference frame, which closely aligns with the robot's reference coordinate. It is necessary to transform the IMU reading from IMU's frame into a global frame.

As shown in Figure 7, we can obtain the transformation between the IMU frame and the global frame, which is calculated as:

{agx=axcos(−θ)−aysin(−θ)agy=axsin(−θ)−ay+cos(−θ)    (24)

Figure 7. Transformation between IMU frame and Global Frame (NED).

4.3.2 State transition model

The state vector of the system in the global coordinate is defined as:

xk=[x,y,vx,vy,θ,ω]    (25)

where xk, yk represent the position of the robot in the global frame. vk and vy represent the velocities. θ and ω mean the heading angle and angular velocities respectively.

In the global coordinate system, the state transition model takes the IMU's readings, including heading θ, angular velocity ω, and the accelerations as the control input. The state transition model (in the NED frame) is then:

x^k|k-1=Fk(xk-1,uk-1)=[xk-1+vxΔk+12agxΔk2yk-1+vyΔk+12agyΔk2vx-1+agxΔkvy-1+agyΔkθkωK]    (26) 4.3.3 Observation model

The GPS observation model produces a prediction of the expected GPS observation based on the predicted state. Here we use the consumer-grade GPS to produce the observation of the displacement. The observation model is expressed as follows:

zk|k-1=Hkx^k|k-1=[100000010000]x^k|k-1    (27) 4.3.4 Noise setting

The initial process noise Qk and measurement noise Rk matrices of the EKF are expressed in Equations 2, 3. These Qk and Rk matrices are determined using empirical data as well as completing experimental tuning. The initial Qk and Rk matrices used in our experiments are developed as follows:

Qk=[1000000100000010000000000100000000000.001000000