and corresponding control inputs U = that minimize a cost function J(Q, U), subject to constraints on dynamics, control inputs, and environmental interactions. The general form of the cost function can be represented as J(Q,U)=∑t=1N(αd(qd,qd)+βc(qd,ut)+γs(qd,O))    (2)

where d(qd, qd) measures the Euclidean distance between the current position qd and the desired state qd, c(qd, ut) represents the control cost associated with the input ut, s(qd,O) is a penalty function for proximity to obstacles O=, and α, β, and γ are weighting factors balancing the trade-offs between reaching the target, control effort, and safety.

To navigate effectively, the robot must satisfy several constraints. Obstacle avoidance requires that at any position qd, the robot maintains a safe distance dmin from all obstacles. For a static obstacle located at os, this is expressed as

||qd-os||≥dmin,   ∀os∈Os.    (3)

For dynamic obstacles, the safe distance must account for their positions od(t) over time, formulated as

||qd-od(t)||≥dmin,   ∀od(t)∈Od.    (4)

The kinematic and dynamic constraints require that the control input ut satisfy the physical limitations of the robot, such as maximum speed vmax and maximum rotational velocity ωmax:

|vt|≤vmax,   |ωt|≤ωmax.    (5)

Boundary constraints ensure that the robot's path remains within the boundaries of the environment E, typically expressed as

xmin≤xt≤xmax,   ymin≤yt≤ymax.    (6)

The control law guiding the robot can be represented as:

ut=f(qd,qt-1,g(x,y),O)    (7)

where f determines the optimal control action ut based on the robot's current state qd, its previous state qt−1, the global path g(x, y) generated by the planner, and the obstacle information O.

To solve this optimization problem efficiently, we propose a hybrid approach using Deep Reinforcement Learning (DRL) for real-time decision-making on navigation steps and Quantum-behaved Particle Swarm Optimization (QPSO) for long-term path optimization. DRL learns a policy π(ut|qd) that maps each state to an optimal action to maximize the cumulative reward, defined as the negative of the cost function J, while QPSO adjusts the paths globally to ensure convergence to a path that meets all constraints and minimizes the total cost over the planning horizon. Achieving a global minimum in nonlinear, high-dimensional optimization problems is inherently challenging. While our approach does not explicitly guarantee a global minimum, it employs a mechanism to enhance global convergence, and QPSO introduces quantum-inspired behavior that enhances global search capabilities. It supports probabilistic exploration, allowing the algorithm to escape from local minima and improve the probability of reaching near-global optimality. The DRL module dynamically optimizes the path and control decisions based on real-time environmental feedback, further reducing the risk of falling into a suboptimal solution.

2.3 Adaptive quantum-enhanced path optimization module

In this section, we present the core component of our proposed RL-QPSO Net: the Adaptive Quantum-Enhanced Path Optimization Module. This module leverages a modified Quantum-behaved Particle Swarm Optimization (QPSO) algorithm, enhanced by reinforcement learning principles, to enable dynamic and efficient path planning in complex environments. The QPSO algorithm here utilizes a quantum-inspired mechanism to allow each particle in the swarm to exhibit probabilistic behavior, aiding in the escape from local optima and improving convergence toward the global optimal path (as shown in Figure 3).

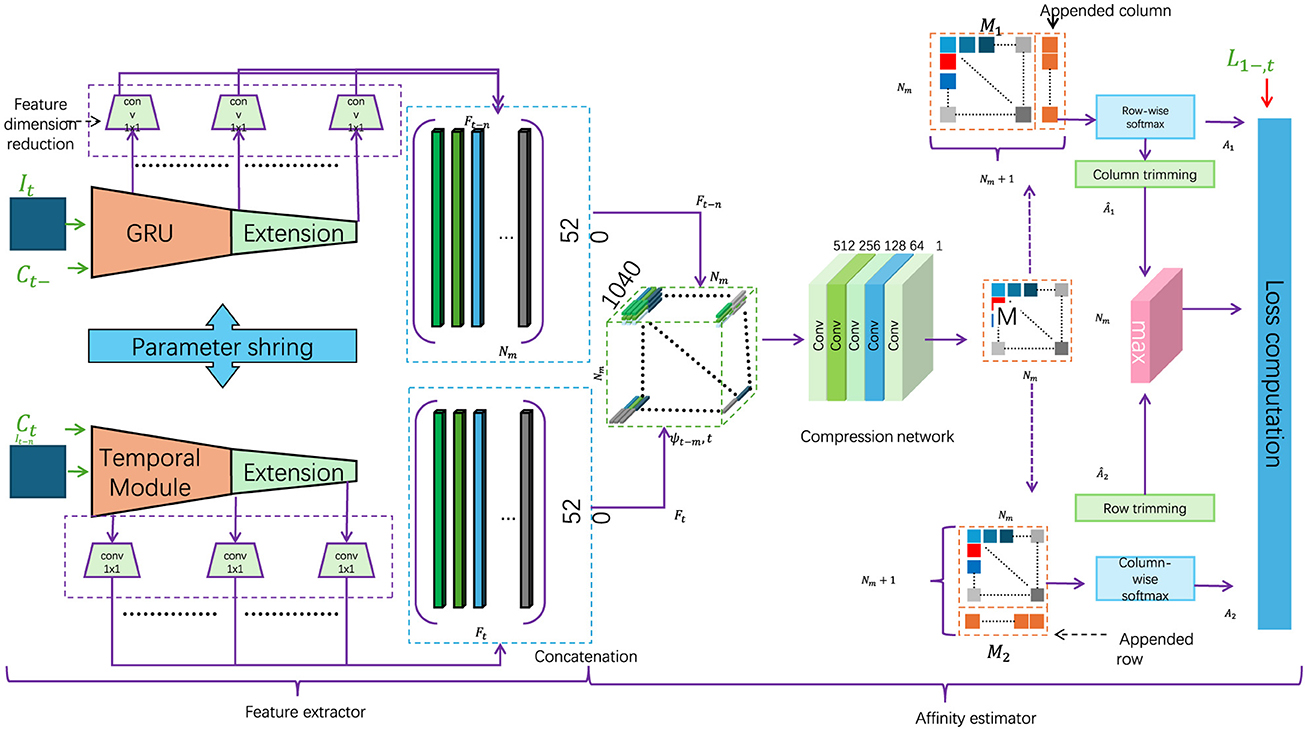
Figure 3. Flowchart of a complex robotic navigation system, employing a context-aware strategy with dynamic environmental adjustments. The diagram illustrates feature extraction processes, temporal modules, and multiple layers of data processing. The architecture integrates environmental priors and a dynamic context evaluation function to optimize robot navigation decisions in varied terrains, highlighted by the real-time adjustments to the robot's path based on the surrounding environmental attributes.

GRU-driven quantum particle dynamics

In the classical QPSO framework, each particle's position is updated according to its historical best position and the global best position within the search space. However, in our adaptive approach, we introduce an augmented particle updating mechanism that incorporates not only positional information but also dynamically adjusted weights informed by the deep reinforcement learning (DRL) layer, further enhanced by a Gated Recurrent Unit (GRU) structure. The GRU enables retention and updating of contextual information over time, allowing the particles to adapt their behavior based on learned environmental patterns. This creates a feedback loop where the QPSO's global search is guided by the DRL module's localized action predictions, facilitating more adaptive path optimization in response to environmental changes (as shown in Figure 3).

In this enhanced QPSO model, the position update rule for particle i is formulated as:

xit+1=pit+λi·sign(gt-xit)·Liln(1ui),    (8)

where:

• xit: position of particle i at iteration t,

• pit: particle's historical best position,

• gt: global best position,

• λi: adaptive weight informed by the DRL layer,

• Li: characteristic length of the quantum potential well,

• ui: uniformly distributed random variable in (0, 1).

The introduction of the GRU structure provides a dynamic mechanism for context-dependent learning, where the internal state of the GRU evolves according to:

hit+1=σ(Wz·xit+Uz·hit+bz)⊙hit            +(1−σ(Wz·xit+Uz·hit+bz))⊙ϕ(Wh·xit            +Uh·hit+bh),    (9)

where:

• hit+1: updated hidden state of the GRU for particle i,

• Wz, Uz, bz: parameters of the update gate,

• Wh, Uh, bh: parameters of the candidate state,

• σ(·): sigmoid activation function,

• ϕ(·): hyperbolic tangent activation function,

• ⊙: element-wise multiplication.

The adaptive weighting factor λi is derived from the GRU's output and the DRL layer's predictions:

λi=γ·fDRL(hit)+(1-γ)·ωi,    (10)

where:

• fDRL(hit): reinforcement learning feedback derived from GRU's hidden state,

• ωi: static weight influenced by environmental heuristics,

• γ: mixing parameter controlling the relative influence of the DRL feedback and static weights.

The quantum potential well length Li dynamically adjusts to reflect the exploration-exploitation tradeoff:

Li=κ·‖gt-xit‖‖gt-pit‖+ϵ,    (11)

where:

• κ: scaling factor,

• ϵ: small constant to prevent division by zero.

These enhancements enable particles to exhibit dynamic, context-aware behavior, achieving a balance between global exploration and local refinement. The feedback loop involving GRU and DRL fosters continuous adaptation, enhancing convergence speed and robustness in dynamic and high-dimensional environments.

Dual-objective reward mechanism

The integration of the DRL layer with the QPSO optimization process enables a dynamic and context-sensitive adjustment of the particle weighting factors λi. The DRL policy π(ut|qt) evaluates the robot's environment and performance in real time, generating a reward signal Rt at each step. This signal dynamically adjusts λi to prioritize either exploration or exploitation depending on the system's needs. The adaptive weighting factor λi is updated using the following rule:

λi=λmin+(λmax-λmin)·exp(-|Rt-Rtarget|σ),    (12)

where:

• λmin and λmax: lower and upper bounds for λi,

• Rtarget: the desired reward threshold representing optimal performance,

• σ: sensitivity parameter controlling the influence of reward deviations on λi,

• Rt: the reward signal derived from the dual-objective reward structure.

This mechanism allows λi to decrease or increase adaptively, fostering a balance between wide-ranging exploration and targeted convergence, depending on whether the observed performance aligns with or deviates from the expected reward.

To further enhance the system's adaptability, the reward function Rt incorporates a dual-objective structure that simultaneously optimizes for path efficiency and safety. This reward function is expressed as:

Rt=-α·d(qt,T)-β·∑j∈Oexp(-γ‖qt-oj‖),    (13)

where:

• d(qt, T): Euclidean distance from the robot's current position qt to the target T,

• oj: position of obstacle j,

• O: set of obstacles in the environment,

• α, β, γ: tunable parameters to balance the importance of path efficiency and safety.

The first term, −α·d(qt, T), penalizes longer paths by incorporating a direct distance measure to the target T. This encourages efficient navigation while minimizing travel time. The second term, -β·∑j∈Oexp(-γ‖qt-oj‖), introduces a safety mechanism by exponentially increasing penalties as the robot nears obstacles. The parameter γ determines the sensitivity of the safety term, enabling fine-grained control over obstacle avoidance.

To ensure the DRL layer adapts to varying operational scenarios, a normalized composite reward signal is introduced:

Rtnorm=Rt-RminRmax-Rmin,    (14)

where:

• Rmin and Rmax: minimum and maximum observed rewards over a fixed time window,

• Rtnorm: normalized reward ensuring consistency across diverse environments.

Finally, a temporal smoothing mechanism is applied to the reward signal to stabilize updates over time, expressed as:

R̄t=η·Rt+(1-η)·R̄t-1,    (15)

where:

• R̄t: smoothed reward at time t,

• η: smoothing factor controlling the influence of recent vs. historical rewards.

This dual-objective reward mechanism empowers the system to dynamically adapt its navigation strategy by balancing path efficiency and safety. The inclusion of adaptive, normalized, and smoothed reward structures ensures robustness in varying and unpredictable environments.

Local refinement for safety and smoothness

Our QPSO algorithm includes an additional local search refinement step to further optimize the path based on real-time feedback. Each particle undergoes a localized adjustment if its positional update leads to potential collisions or suboptimal paths. This is governed by a gradient-based adjustment rule:

xit+1=xit+1-η∇J(xit+1),    (16)

where η is a learning rate and ∇J(xit+1) denotes the gradient of the cost function J at the updated position xit+1. This local refinement enables the model to adaptively fine-tune the path, improving response to environmental changes and mitigating abrupt deviations, thereby ensuring smoother and safer navigation paths.

Our method adopts an improved quantum behavioral particle swarm optimization (QPSO) algorithm and is enhanced by reinforcement learning principles. It is mainly used for path planning in dynamic and complex environments rather than traditional neural network training methods. The reason we chose QPSO is that it has strong global search capabilities and the potential to escape from local optimality. Especially in non-convex optimization problems such as path planning, this feature can significantly improve search efficiency. In addition, our improved version of QPSO combines the dynamic weight adjustment and environment awareness capabilities of deep reinforcement learning (DRL), further improving the ability to adapt to dynamic environmental changes, while traditional neural network training methods are difficult to directly apply to such problems. This design has been verified in experiments to have significant advantages in global search capabilities and dynamic adaptability for path optimization.

2.4 Context-aware strategy for path reliability

To further improve the efficiency and robustness of RL-QPSO Net, we integrate a context-aware strategy that leverages environmental priors and domain-specific knowledge. This strategy enables the model to dynamically adjust its path planning behavior based on real-time analysis of the surrounding context, optimizing the robot's navigation decisions according to both immediate and anticipated environmental conditions (as shown in Figure 3).

2.4.1 End-to-end contextual integration

The context-aware strategy introduces dynamic environmental adjustments to guide the robot's navigation and interaction within complex terrains. Central to this strategy is a weighting mechanism that modifies the reward and cost functions based on the robot's spatial relationship to specific environmental attributes, such as bottlenecks, high-risk zones, and dynamically moving obstacles. To operationalize this, a contextual evaluation function C(pt,S) is defined, where pt represents the robot's position at time t, and S encompasses the spatial and dynamic characteristics of the environment.

An adjusted reward function incorporating these contextual dynamics is given by:

Rtadjusted=Rt+λ·C(pt,S),    (17)

where: Rt is the baseline reward reflecting fundamental navigation priorities such as path optimality and obstacle avoidance, λ is a scaling factor that modulates the impact of contextual information, and C(pt,S) is the contextual influence evaluated at the current position.

To further adapt the model for dynamic environments, an auxiliary penalty term is introduced to incorporate uncertainty and risks associated with real-time environmental fluctuations:

Ptcontext=α·σ(∇C(pt,S))+β·η(S),    (18)

where:

• σ(·) represents a spatial gradient function evaluating abrupt changes in the context function, highlighting high-risk transitions,

• ∇C(pt,S) denotes the gradient of the contextual influence,

• η(S) assesses global environmental volatility, such as obstacle velocities or density changes,

• α and β are tunable parameters for risk balancing.

The overall objective function for decision-making integrates the reward and penalty components:

Ft=maxut[Rtadjusted-Ptcontext],    (19)

where ut denotes the control inputs at time t, optimized for balancing contextual rewards against environmental penalties.

2.4.2 Multi-factor context function for diverse environmental adaptation

The context function C(qt,E) is modeled as a weighted sum of multiple environmental factors, each represented by a contextual sub-function Ck(qt), which addresses specific navigation considerations. This can be written as

C(qt,E)=∑k=1K