1 Introduction

Human beings possess a remarkable capacity to discern physical characteristics of grasped objects, such as stiffness and shape, from the sensory signals of the hand with a high degree of freedom. Furthermore, but they are also able to recognize their confidence in the estimated object properties, which they use for manipulation and further exploration. For example, humans are able to recognize the shape of an object by touching it. When the shape is unclear at the first touch, they recognize it and touch the object again to make sure where to grasp. When the grasped object is likely to be soft and fragile, humans would grasp it conservatively based on the degree of uncertainty in the rigidity. These abilities are essential to realize robotic hands that are capable of performing stable grasping and manipulation.

Object properties can be classified into two distinct types of categories: geometric properties and physical properties (Wang et al., 2020). The geometric properties include the position, pose, shape, etc., whereas the physical properties include the mass, stiffness, texture, etc. Estimating both types of properties is essential for proper object manipulation. For example, the geometric properties provide the necessary posture of the hand necessary to grasp the object and maintain its form closure, which is crucial for stable grasping, while the physical properties determine the maximum amount of grasping force the robot can exert without breaking the object. Robots need to know those properties from sensory information unless those properties were given in advance. However, putting multiple various sensors on the hand can increase the cost. Thus, it is preferable to estimate the object properties from proprioceptive information, such as finger joint angles, which can be measured in most cases for joint control.

There are studies regarding the estimation of geometric and physical properties with robotic hands (Wang et al., 2020; Spiers et al., 2016; Gao et al., 2016). However, in contrast to estimation of geometric properties. It has been widely researched that the estimation of physical properties or combining them with geometric-property estimation is not fully researched. There exist numerous methods for estimating physical-property. The estimation of stiffness necessitates the utilization of additional sensors for force measurements (Kicki et al., 2019; Spiers et al., 2016), resulting in an increase in costs and mechanical complexity. Furthermore, it has been observed that stiffness estimation is typically performed solely once at the terminal time step (Bednarek et al., 2021). For adaptive grasping and dexterous manipulation, robotic hands need to estimate both types of object properties in real time in order to adjust grasping force.

When a robotic hand estimates object properties from proprioception in real time, it is important to handle uncertainty as this task requires to estimate from limited information. For example, it is impossible to estimate the objects' properties of objects before contact, which results in the epistemic uncertainty, which is caused by lack of knowledge. Furthermore, observation noises in sensory signals degrade the quality of estimation, resulting in the aleatoric uncertainty, which is due to randomness. Without estimating those uncertainties, robots would make incorrect decisions based on unreliable estimates that could have been avoided with further exploration and conservative actions. Another issue that arises when estimating object is the necessity of weight parameters in the loss function to balance the scales of the multiple properties, which that is a time-consuming process.

To address the above issues, this study introduces a method to estimate both geometric and physical properties using confidence factors, which measure uncertainty. We develop design a learning framework based on probabilistic inference and apply the method to neural networks with a robotic hand without tactile sensors in simulation. In the framework, we utilized a loss function without hyper-parameters and a time-series chunking technique that could improve learning stability. Neural networks are implemented to generate the variance of the estimated stiffness, which value can be regarded as the confidence level of estimation. Although neural networks outputting variance are not novel (Nix and Weigend, 1994), we apply this approach to object-property estimation with a multi-fingered robotic hand and demonstrate its effectiveness to this task. Contributions from of this study are listed below.

1. We have developed a framework that enables for robotic hands to assess stiffness and shape of an object, incorporating their uncertainty.

2. We designed a loss function without hyperparameters in order to balance the scales between different properties.

3. We demonstrate that trained neural networks are capable of estimating the stiffness and the shape by utilizing proprioceptive signals, while also estimating the confidence level of estimation, taking into account and task difficulty, such as variance and entropy.

2 Materials and methods 2.1 Overview

We consider a situation where a robotic hand grasps an object with pre-defined control commands and estimates the object's properties, particularly its stiffness and the shape. The robot hand is capable of measuring joint angles and joint angular velocity, but it does not have visual sensors, tactile sensors, or force sensors. We finally develop neural networks that generate estimates of the object's properties sequentially.

We define mathematical symbols as follows. Let the stiffness be expressed as a scalar value k>0, and let the shape be expressed as a discrete label s∈S≜, where C denotes the number of classes. Furthermore, it is recommended that the joint angles, joint angular velocities, and joint angle commands be designated as q∈ℝD, q·∈ℝD, and qcmd∈ℝD, respectively, where D denoting the degrees of freedom (DoF). We occasionally refer to observations as y≜[q,q·,qcmd]⊤∈ℝ3D for simplicity.

2.2 Training strategy

In many studies, the root mean square errors (RMSEs) are used to estimate continuous values. However, there are a few that make the object property estimation difficult:

1. It is impossible in principle to estimate the properties of an object properties before contact with the object, resulting in the epistemic uncertainty. RMSEs are unable to handle such kind of uncertainty.

2. As neural networks are capable of estimating multiple types of properties with varying units and different representations (e.g., continuous values or discrete labels), such as weight constants are typically required to balance the estimation errors among various types of properties. The cost of designing weight constants increases with the increase in the number of properties.

To address the above issues, we designed the estimation task as a probabilistic inference. Probabilistic inference can naturally express the uncertainty of the object's properties that happens before touch. Furthermore, by considering the task as a likelihood maximization problem, it can be transformed into probabilistic inference of a single joint distribution of multiple properties, which does not have weight constants.

Concretely, the object property estimation task is formulated as the following optimization problem:

maximizeθnk,θns∏n=0N-1p(kn,sn|θnk,θns).    (1)

Here, N and n indicate the dataset size and the index of samples in the dataset. θnk and θns indicate the parameters of the probabilistic distributions of the stiffness and the shape, respectively. θnk and θns can be regarded as estimation results of kn and sn in a statistic way. We then consider its negative log-likelihood as follows:

-log∏n=0N-1p(kn,sn|θnk,θns)=∑n=0N-1-logp(kn,sn|θnk,θns).    (2)

Thus, the optimization problem can be equivalently converted as follows:

minimizeθnk,θns∑n=0N-1[-logp(kn,sn|θnk,θns)].    (3)

We assume each negative log-likelihood term can be decomposed as follows:

-logp(kn,sn|θnk,θns)=-log[p(kn|θnk)p(sn|θns)]         =-logp(kn|θnk)-logp(sn|θns)    (4)

We also model the probabilistic distribution of the stiffness as a Gaussian distribution as follows:

-logp(kn|θnk)=-logp(kn|μn,σn2)       =-log(12πσn2exp[-(kn-μn)22σn2])       =(kn-μn)22σn2+logσn+12log(2π)    (5)

Here, the parameter is expressed as θnk≜(μn,σn2), where μn and σn2 indicate the mean and the variance. On the other hand, the probabilistic distribution of the shape is modeled as a discrete distribution obtained through the softmax function as follows:

-logp(sn=Sc|θns)=-logp(sn=Sc|zn(1),…,zn(C))          =-logexpzn(c)∑c′=1Cexpzn(c′)    (6)

Here, the parameter is expressed as θns≜(zn(1),…,zn(C)), where zn(c)∈ℝ for all c = 1, …, C. The above equation corresponds to the cross-entropy. Hereinafter, we use zn≜[zn(1),…,zn(C)]⊤ and CE(sn,zn)≜-logp(sn|θns).

Finally, the optimization problem is converted as follows:

minimizeμn,σn,zn∑n=0N-1[(kn-μn)22σn2+logσn+CE(sn,zn)].    (7)

This can be computed by minimizing the following learning loss:

L≜1N∑n=0N-1[(kn-μn)22σn2+logσn+CE(sn,zn)].    (8)

It is noteworthy that the learning loss L lacks any hyper-parameters, such as weight constants. Instead, σn behaves as a weight balancing the RMSE of the stiffness (kn-μn)2 and the classification errors of the shape CE(sn, zn). Unlike a constant weight, σn itself is to be optimized by the term of logσn, resulting in a statistically optimal value.

2.3 Estimation with neural networks

We develop a neural network architecture that estimates parameters such as θnk and θns from a time series of observations. A simple approach is to use recurrent neural networks that receive observations y for each time step. However, it may lead to too deep layers in time, which may result in unstable learning, high computational cost, and slow inference. Therefore, we treat a time series of raw observations with a high sampling rate as a time series of chunks with a low sampling rate (Kutsuzawa et al., 2017, 2018). Similar techniques have also been employed in a Transformer-based model for robotic imitation learning (Zhao et al., 2023). Concretely, we transformed a time series (y[0], y[1], …, y[t], …, y[T−1]) into (Υ[0], Υ[1], …, Υ[λ], …, Υ[Λ−1]), where

Υ[λ]≜[y⊤[λK],y⊤[λK+1],…,y⊤[(λ+1)K-1]]⊤∈ℝ3DK.    (9)

Here, K∈ℕ indicates the chunk size. Finally, the time-series length of T can be reduced to a shorter length Λ=TK∈ℕ, where ⌈•⌉ indicates the ceiling function. This technique can reduce the time-series length approximately K times shorter, making learning more stable with a lower computational cost. Although it also reduces the estimation frequency, it does not matter in many cases as estimation usually does not require a high update frequency. Although chunking may limit the representation ability of the model, it would be better than down-sampling, which is similar to chunking but decimates the data samples. Thus, it is anticipated that this chunking technique yields more advantages than disadvantages. This technique is graphically shown in Figure 1.

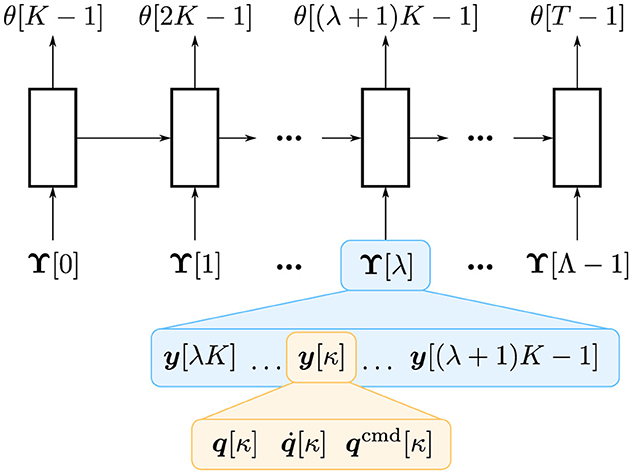
Figure 1. Overview of time-series chunking. A recurrent neural network, illustrated as blocks, receives Υ[λ] that consists of K observations: (y[λK], y[λK+1], …, y[(λ+1)K−1]). θ[t] indicates the estimated parameters of the stiffness and the shape at the t-th time step, i.e., θ[t] = (θk[t], θs[t]).

A neural network generates the values of, μ, logσ2, and z. Here, we use logσ2 instead of σ or σ2 as a primitive term because logσ2 can take −∞ to ∞, making it more manageable for a linear-combination layer. Therefore, in practice, the learning loss defined in Equation 8 is transformed as follows:

L=1N∑n=0N-1[(kn-μn)22exp(logσn2)+12logσn2+CE(sn,zn)].    (10) 2.4 Evaluation setup

We used a MuJoCo (Todorov et al., 2012) implementation of Allegro Hand, implemented by Zakka et al. (2022), as shown in Figure 2. We controlled flexion motion at the joints; 11 degrees of freedom were obtained. The entire process is controlled.

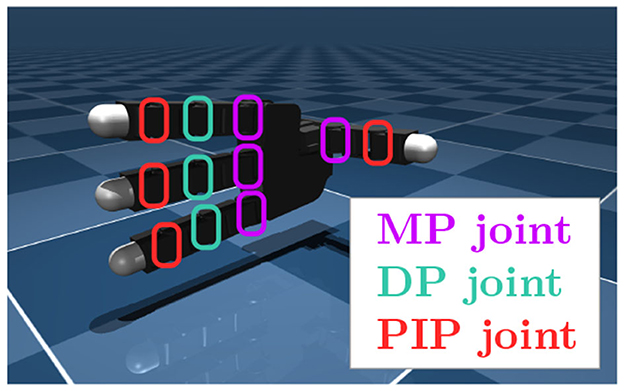
Figure 2. Allegro Hand and its joint definitions.

We employed three distinct categories of target objects: cylinder-shaped objects, box-shaped objects, namely sphere-shaped objects, as shown in Figure 3. An object was modeled as a composite of small capsule elements connected by springs each other. The object stiffness was determined by specifying the spring stiffness connecting the elements. Objects were fixed to the space to avoid falling out of the hand. Note that this study focuses on the object property estimation.

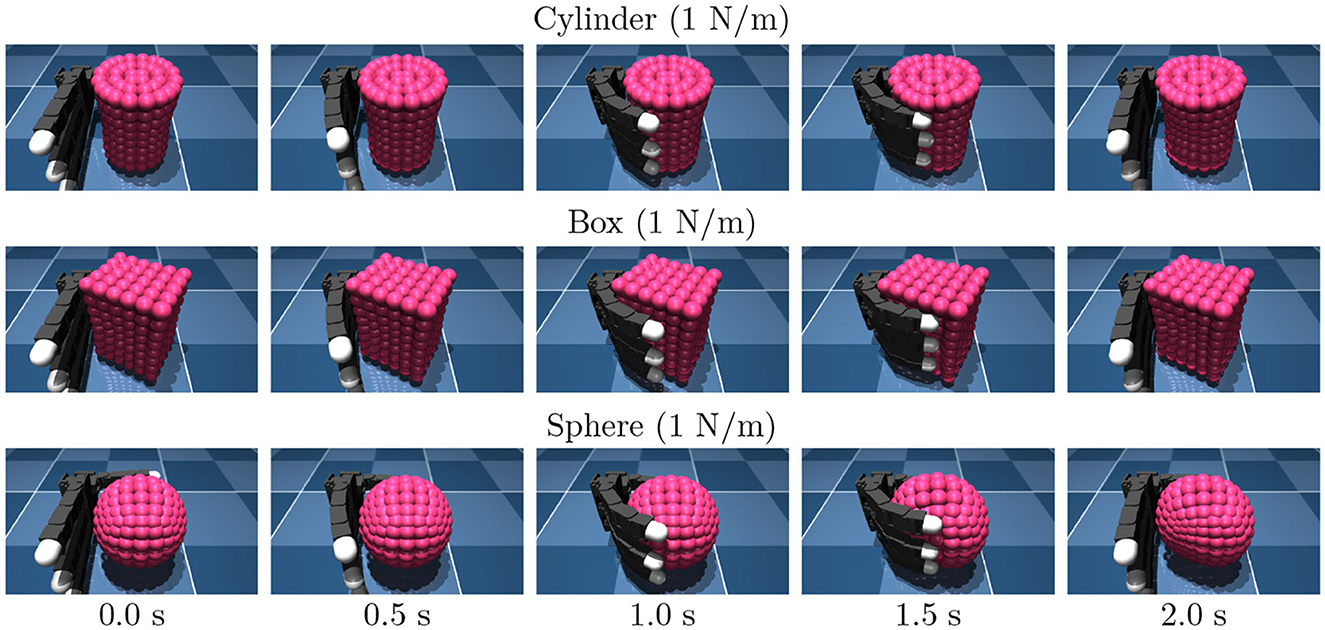
Figure 3. Snapshots of the training data.

For data collection, we controlled the robotic hand with a PD positional controller for 2.2 s with predefined joint angle commands as described in Table 1. For each episode, we recorded a time series of 33-dimensional data that consists of joint angles, joint velocity, and joint angle commands. The observation was measured. The delay is set to 1 ms. Examples of data are shown in Figure 4.

Table 1. Profile of joint angle commands.

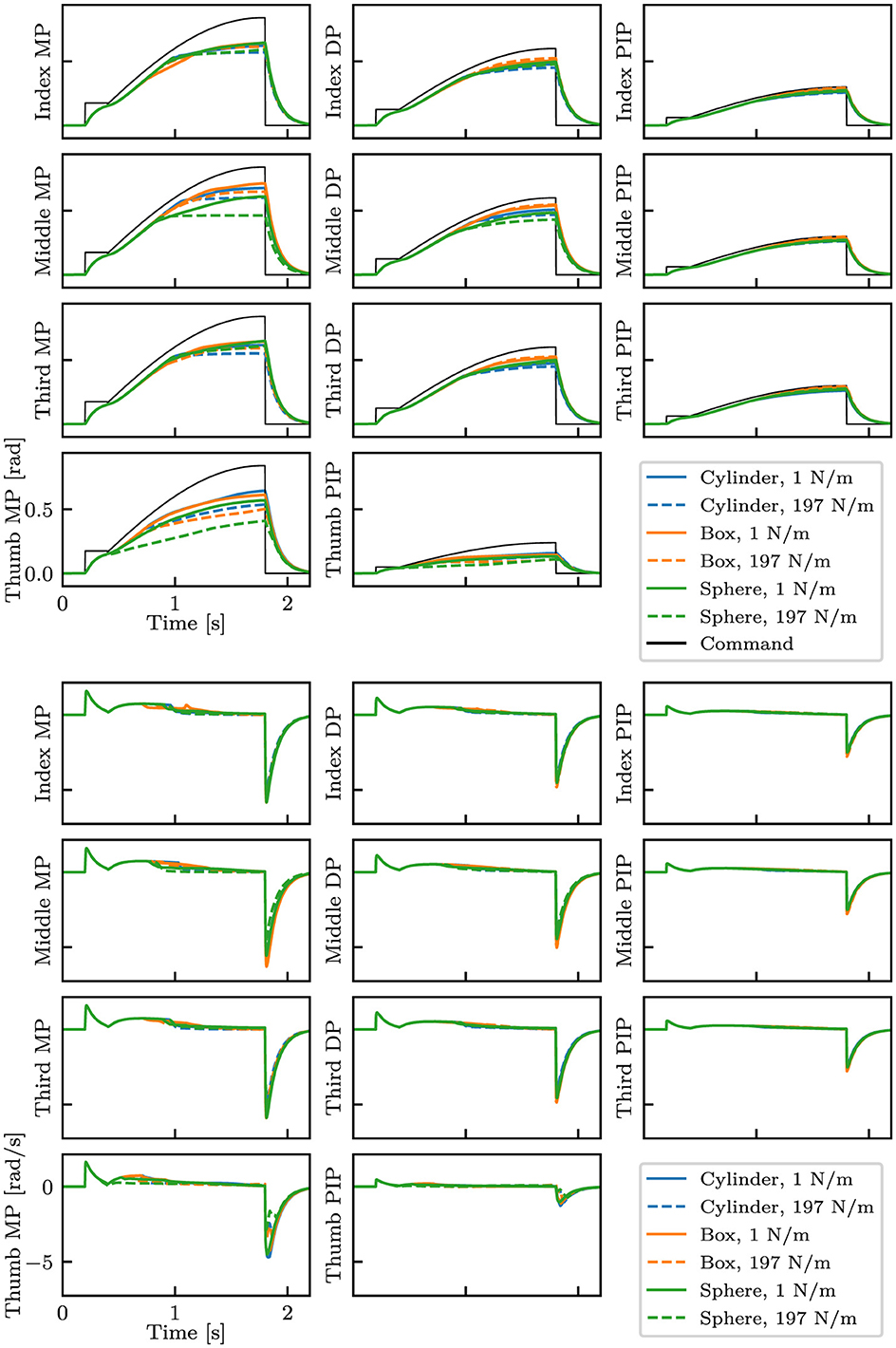
Figure 4. Examples of collected data with different shapes and stiffness. The top eleven plots show the finger joint angles and the commands, whereas the bottom eleven plots show the angular velocity of the joints. Three types of objects with the smallest (1 N/m) and highest (197 N/m) stiffness are shown.

We collected data with the three types of objects, while varying the stiffness with the range from 1 to 197 N/m in 4 N/m increments and varying the position and the orientation in 10 random values in the range of ±5 mm and ±5 deg, respectively; 1,500 data were collected in total. We call this dataset the standard dataset; we use this dataset for training unless otherwise specified. Seventy percentage of the dataset was used for training, and the remaining 30% were used for validation. During the course of training, we introduced Gaussian noises ε~N(ε;0,σ) to q and q·, while varying σ as log10σ~U(log10σ;-4,-1) for each mini-batch; here, U(x;a,b) denotes a uniform distribution of x within the range of a ≤ x<b.

In order to evaluate the model's ability to handle diverse data, we prepared another training dataset with varying object sizes and positions/orientations. In addition to the configuration of the standard dataset, objects of varying sizes are incorporated. This dataset comprises of 4,500 data points (1,500 data points each for the normal, bigger, and smaller sizes). We refer to it as a full dataset.

We used a neural network architecture as illustrated in Figure 5. It consists of a recurrent layer with long short-term memories (LSTMs) with 256 units, followed by a dropout layer with a dropout rate of 0.5 and a full-connection layer. For learning stability, we calculate μ as follows:

μ= 200·μ~+12,    (