1 Introduction

Visual place recognition (VPR) refers to the capability of identifying locations within a physical environment solely through visual inputs. It is essential for autonomous navigation of mobile robots, indoor assistive navigation aid, augmented reality, and geolocalization (Lanham, 2018; Reinhardt, 2019; Weyand et al., 2016; Seo et al., 2018; Li et al., 2018; Shan et al., 2015). These applications generally involve complex dynamic scenes, perceptual aliasing, viewpoint and appearance variation, which render VPR extremely challenging.

VPR has been approached via deep learning techniques (Radenović et al., 2018; Chen et al., 2017; Sünderhauf et al., 2015) and through various supervised and self-supervised feature descriptor representations (DeTone et al., 2018; He et al., 2018; McManus et al., 2014). Despite their promise, many of these methods face significant practical challenges (Lynen et al., 2015, 2020). For example, they often rely on large, deep networks with time-consuming training processes and dense feature extraction, ultimately making them computationally expensive, memory-intensive, and energy-demanding. Such limitations significantly reduce the ability for real-world deployment of conventional artificial neural networks (ANNs) on robotic platforms with limited on-board resources (Doan et al., 2019). Spiking neural networks (SNNs) offer an alternative with their remarkable potential for computationally efficient operation when they are implemented on neuromorphic hardware (Davies et al., 2021). However, previous work on SNN models for VPR has suffered from scalability problems that impede their application to data with a large number of locations. In addition, the majority of the aforementioned methods formulate VPR as an image retrieval task (Garg et al., 2021), the solution of which aims for the correct association of given query images with a set of reference images. Such formulation requires the employment of a confusion matrix (a.k.a. distance matrix) (Garg et al., 2022) populated with similarity scores based on the distances between model-specific feature descriptors. A commonly-used similarity metric is the cosine similarity (Naseer et al., 2018), which is reported to be computationally expensive when evaluating high-dimensional feature vectors (Zhang et al., 2021).

These drawbacks have motivated our approach to VPR, described in this paper, in which an SNN model is implemented using an ANN-to-SNN conversion method to enable backpropagation-based training, resulting in fast training and inference times. We employ a smooth rate-based approximation (Hunsberger and Eliasmith, 2015) of the leaky integrate-and-fire (LIF) neurons (Burkitt, 2006) during the training. Once the training session is completed the rate-based units are substituted with the spiking LIF neurons and the resulting spiking network is used for inference.

We formulate VPR as a classification task, where the SNN model predicts place labels that uniquely correspond to the locations in a discretized navigation domain. We evaluate our method with the challenging real-world benchmark datasets Nordland (Olid et al., 2018) and Oxford RobotCar (Maddern et al., 2017, 2020). Our model, the Localizing Convolutional Spiking Neural Network (LoCS-Net), outperforms other SOTA SNN-based VPR methods on both the Nordland (Olid et al., 2018) and the Oxford RobotCar dataset (Maddern et al., 2017, 2020) in terms of precison at 100% recall (P@100%R).

The main contributions of this work are as follows. (a) To the best of our knowledge, LoCS-Net is the first SNN that is trained to perform the VPR task by means of ANN-to-SNN conversion and backpropagation. (b) LoCS-Net is an end-to-end SNN solution. Therefore, LoCS-Net does not require further processing of its outputs for recognizing places. In that sense, LoCS-Net saves all the computation resources that traditional VPR algorithms would typically expend on feature encoding, descriptor matching, computing similarity scores, and storing a distance matrix. (c) We demonstrate that our proposed SNN model yields the fastest training time, the second fastest inference time, and the best VPR performance in P@100%R among its SNN counterparts. This poses LoCS-Net as a significant step toward deployment of SNN-based VPR systems on robotics platforms for real-time localization. (d) We report the challenges we experienced when deploying LoCS-Net on the neuromorphic Loihi chips in detail. We strongly believe that our in-depth discussion on hardware deployment will be useful for the SNN-VPR community.

2 Related work

Task-specific feature descriptors are the very core of traditional VPR systems, which can be grouped into two categories: (1) Local descriptors, (2) Global descriptors. Local descriptors may scan the given images in patches of arbitrary size and stride. These patches are then compared to their immediate neighborhood to determine the distinguishing patterns (Loncomilla et al., 2016). In general, previous VPR work utilizing local descriptors (Johns and Yang, 2011; Kim et al., 2015; Zemene et al., 2018) employs sparse filters that extract so-called key-points (Mikolajczyk and Schmid, 2002; Matas et al., 2004). These key-points can be marked by the descriptions generated through the application of methods including SIFT (Lowe, 1999), RootSIFT (Arandjelović and Zisserman, 2012), SURF (Bay et al., 2006), and BRIEF (Calonder et al., 2011). In this way, the combination of heuristics-based detectors and local descriptors can be used for: (A) Representing images, (B) Comparing two images with respect to their descriptors to determine how similar they are. In addition, local features can be combined with other embeddings (Tsintotas et al., 2022) while leveraging their robustness against the variations in the robot's pose. However, local descriptors can be computationally heavier and more sensitive to illumination changes (Masone and Caputo, 2021). Global descriptors (Oliva and Torralba, 2006; Torralba et al., 2008), on the other hand, do not require a detection phase and directly encode the holistic properties of the input images. Although this might save the global descriptor-based VPR methods (Liu and Zhang, 2012; Schönberger et al., 2018; Revaud et al., 2019; Yin et al., 2019) some compute time, they are more vulnerable to robot pose changes than their local descriptor-based counterparts while being inept at capturing geometric structures (Dube et al., 2020). Yet, global descriptors are reported to be more effective in the case of varying lighting conditions (Lowry et al., 2015). Furthermore, there are hybrid approaches (Siméoni et al., 2019; Cao et al., 2020; Hausler et al., 2021), which combine the strengths of both approaches.

Deep learning has made key contributions to recent work on VPR. An influential deep-learning-based approach is NetVLAD (Arandjelovic et al., 2016), which is a supervised method for place recognition, based on the Vector of Locally Aggregated Descriptors (VLAD), a technique to construct global image feature representations from local feature descriptors. NetVLAD uses a pre-trained feature extraction network, such as AlexNet (Krizhevsky et al., 2017), to extract the local features, and a loss function that aims to minimize the distance between a baseline input and the most similar image (the positive example), while maximizing the distance between baseline input and the most dissimilar image (the negative example). This loss function is also known as the triplet loss function. Several authors have extended NetVLAD in different directions, and NetVLAD-based methods still perform very competitively (Hausler et al., 2021; Yu et al., 2020).

SNNs have been of interest for various robotics tasks, including not only VPR, but also object detection (Kim et al., 2020), regression (Gehrig et al., 2020), and control of aerial platforms (Vitale et al., 2021) due to their significant potential for computational efficiency (Zhu et al., 2020). Published VPR methods based on SNNs are relatively recent, compared to other robotics research areas. Among them, Hussaini et al. (2022) is reported to be the first high-performance SNN for VPR. There, the authors propose a feed-forward SNN, where the output neuron activations are filtered through a custom softmax layer. Follow-up work by the same authors (Hussaini et al., 2023) introduced a framework where localized spiking neural ensembles are trained to recognize places in particular regions of the environment. They further regularize these networks by removing output from “hyper-active neurons,” which exhibit intense spiking activity when provided with input from the regions outside of the ensemble's expertise. This framework yields a significant improvement over its predecessor while demonstrating either superior or competitive VPR performance compared to the traditional methods. A recent study by Hines et al. (2024) presented an SNN model composed of an ensemble of modified BliTNet (Stratton et al., 2022) modules, each tuned to specific regions within the navigation domain. During training, spike forcing is utilized to encode locations uniquely, which are later identified by monitoring the output neuron with the highest spike amplitude. The authors report remarkable improvements in both training and inference times, alongside achieving superior or comparable VPR performance compared to earlier SNN models. However, training of these SNN approaches do not scale with the increasing volume of training data. In addition, heuristics such as the assignment of neural ensembles to spatial regions, nearest neighbor search in the similarity matrix, and the regularization process further complicate the training process and the computational efficiency of the model. In contrast to these previous SNN-based approaches, we propose an end-to-end solution that is much easier to train and to deploy without requiring heuristic training.

3 LoCS-Net model for visual place recognition

Here, we begin with an overview of the task formulation and the architecture of LoCS-Net in Section 3.1. Section 3.2 formally poses the VPR problem as a classification task. Then, in Section 3.3, we walk through the LoCS-Net pipeline and its key design choices. Moreover, Section 3.3 provides a summary of the ANN-to-SNN conversion paradigm while elaborating on its use for the present work. We would like to refer the readers to the supplementary information and to the figshare repository of our code for further implementation details: https://figshare.com/s/c159a8680a261ced28b2.

3.1 Overview

Figure 1 depicts the overall architecture of LoCS-Net. The input to the model is a set of images sampled along a trajectory that traverses a bounded navigation domain. The domain is discretized by means of a uniform grid (orange lines in Figure 1) and each image is assigned an integer place label based on the tile traversed at the time of sampling the image. In this manner, we define the VPR task as a classification problem as discussed in Section 3.2.

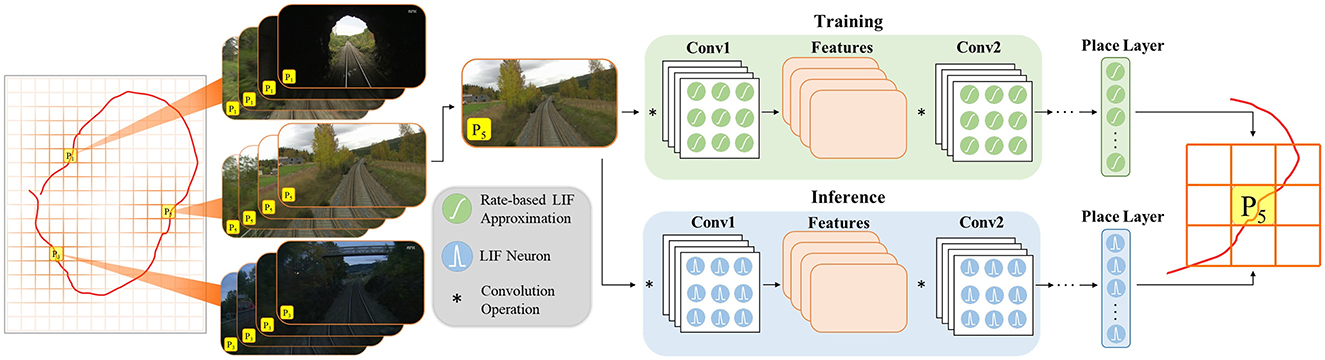
Figure 1. LoCS-Net VPR system: a convolutional network of rate-based LIF neurons (Hunsberger and Eliasmith, 2015) is trained over a set of annotated images sampled over a trajectory (the red curve) traversing a finite discretized (orange grid bounded by gray lines) navigation domain. The VPR task is formulated as a classification problem where each tile of the grid (P1, P2, P3, …) corresponds to a distinct location. After training, the LIF approximations are substituted with the spiking LIF neurons (Burkitt, 2006) for the inference step.

Each layer in the LoCS-Net model consists of LIF neurons (Burkitt, 2006). In order to train the model, these neurons are converted to rate-based approximations of LIF units (Hunsberger and Eliasmith, 2015). Rate-based LIF approximations are continuous differentiable representations of the LIF activation function. The LIF activation function describes the time evolution of the neuron's membrane potential, and it is discontinuous: when the membrane potential reaches a threshold value, it is reset back to a pre-determined state. The rate-based approximation is a continuous function that describes the neuron's firing rate as a function of its input, enabling the use of back-propagation algorithms for training. However, this doesn't prevent the substitution of the approximate LIF neurons with the original ones for inference after the training is complete. A number of authors have reported successful applications (Rueckauer et al., 2017; Hu et al., 2021; Patel et al., 2019) of ANN-to-SNN conversion.

3.2 VPR as a classification task

A common practice in approaching the VPR task is to pose it as an image retrieval problem where the goal is to compute and store descriptors that would effectively encode both the set of query images and the collection of reference images to match (Lajoie and Beltrame, 2022). The encoding process is followed by an image retrieval scheme, which is based on comparing query embeddings (zq) to the database of reference descriptors (zr) with respect to the customized similarity metrics. Nevertheless, computation of the descriptors is numerically expensive. In contrast, we formulate the VPR task as a classification problem in order to bypass the encoding phase of the images. We designed the LoCS-Net so that it would uniquely map the given input images to the mutually exclusive classes, which are the distinct places, as discussed in Sections 3.1, 3.3.

Figure 2 illustrates how our work formulates VPR differently compared to the image retrieval VPR formulation. We first discretize the navigation domain by using a uniform rectangular grid (Figure 2B, the orange lines). Here, each tile of the grid defines a distinct place Pi, i = 1, 2, 3, ⋯ . We would like to note that the navigation domain can be any physical environment with points described by spatial coordinates. Although we use a uniform rectangular grid to discretize the top-down view of the domain of interest, our approach is flexible with respect to the definition of places, and permits 3-D as well as 2-D discretization. As one of many ways to generate the training and test data, we sample images over numerous trajectories traversing the discretized navigation domain. Suppose that an image s∈S is sampled at the time instant when the camera is in the region represented by tile P5. Then, this image would be annotated by the place label 5∈Y. Namely, the image s belongs to the class represented by the tile P5. Thus, given a query image, our goal is to train a spiking neural network model that would correctly infer the associated place labels. Hence, we pose the VPR task as an image classification problem in this fashion. We now formally describe the VPR task as a classification problem as follows.

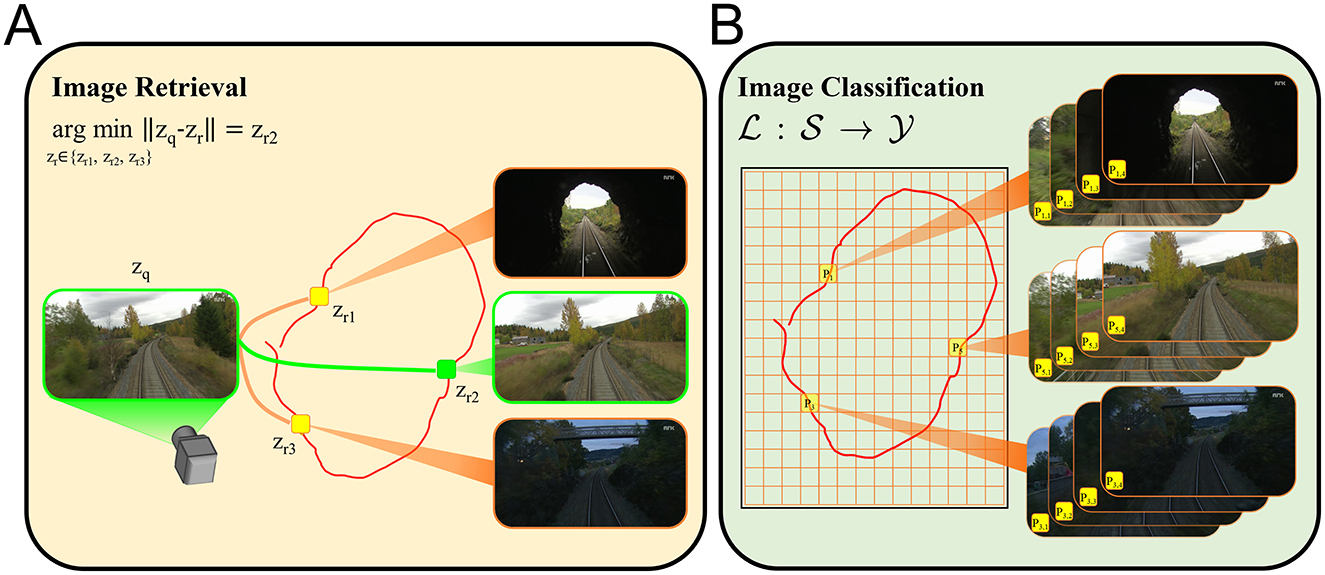
Figure 2. VPR can be posed as image retrieval task or image classification problem. For both formulations we consider a set of images collected over a trajectory (the red curves) traversing a finite navigation domain. (A) A popular VPR solution is based on generating descriptors for query (zq) and reference images (zr), which are then compared to each other in terms of a distance (or similarity) metric ∥·∥ in order to retrieve the reference image corresponding to the correct place. For instance, zr2 represents the most similar reference image to the given query image. (B) In contrast, the image classification formulation of the VPR task requires an arbitrary discretization of the navigation domain to define the classes Pi (the places where i∈Y) that annotate the images s∈S. Then, a classifier L is trained to map images s∈S to the correct place labels i∈Y. The image annotation Pi, j denotes the jth image associated with the class Pi.

Consider a set of images, S=, where C is the number of color channels, H and W are the height and width of the images in pixels and D is a pre-determined finite horizontal navigation domain. Here, X:S→D is a function that maps the images s∈S to the planar spatial coordinates [xs,ys]T∈D= where xmin, xmax, ymin, and ymax are the bounds of D. X(s) describes the in-plane spatial state of the camera with respect to a local frame of choice when s∈S is sampled. The set Y= contains the place labels that annotate s∈S where NP is the number of assumed places. Each y∈Y corresponds to a Py⊂D such that Py∩Pi≡∅,y≠i∧i∈Y. We formulate the VPR task as an image classification problem, where each class is assumed to be mutually exclusive. That is, each image belongs exactly to one class. Our goal is to design a mapping L:S→Y that correctly predicts the place label y∈Y of any given s∈S. One should note that the approach we describe here is different than the image retrieval formulation as we want L to predict the place labels instead of directly associating the input images with the reference images.

3.3 Localizing convolutional spiking neural network

The design of LoCS-Net is defined mainly by two ideas: (1) Discretization of the given finite navigation domain, (2) Leveraging the back-propagation algorithm by adopting the ANN-to-SNN conversion paradigm. We now walk through the details of these ideas together with the architecture of LoCS-Net and its building blocks, LIF neurons.

3.3.1 The LIF neuron model

Unlike standard artificial neurons, which are defined by time-independent differentiable non-linear transfer functions with continuous outputs, spiking neurons have time-dependent dynamics that aim to capture the information processing in the biological neural systems by emitting discrete pulses (Burkitt, 2006). Equation 1 describes the dynamics of an LIF neuron.

Cmdν(t)dt=-Cmτm[ν(t)-ν0]+Is(t)+Iinj(t)    (1)

where Cm is the membrane capacitance, τm is the passive membrane time constant, and ν0 is the resting potential. Above formulation considers a resetting scalar state variable, the membrane potential ν(t), which will be reinitialized at ν(t) = νreset after reaching a threshold, ν(t) = νth. Whenever the re-initialization happens at time t = tspike, the output of the LIF neuron (o(t)) will be an impulse signal of unity. We name this a spike event. One can express a spike event of an LIF neuron by Equation 2, which incorporates Dirac's delta function centered at the time of re-initialization.

o(tspike)=δ[ν(tspike)-νth]    (2)

The right hand side of Equation 1 includes three terms: (1) An exponential decay term (a.k.a the passive membrane leak), (2) Is(t), the sum of incoming synaptic currents, which are mostly unit impulses filtered through a first order delay and/or multiplied by some scalar, and finally (3) An injection term, Iinj(t), that describes the input currents other than synaptic currents. This can be some bias representing the background noise in the corresponding neural system, or just some external input.

Solving the sub-threshold dynamics described by Equation 1 for the firing rate ρ[Is(t)] of an LIF neuron and assuming Iinj(t) = 0 for all t≥0 yields the following.

Tspike=-τmlog(1-(νth-νreset)Cmτm(ν0-νreset)Cmτm+Is(t))    (3) ρ[Is(t)]=-1;  Θ(x)=γlog(1+ex/γ)    (5)

where γ is the smoothing factor of choice.

3.3.2 ANN-to-SNN conversion

Due to the discontinuities introduced by discrete spike events, the conventional gradient-descent training techniques need to be modified for spiking neural networks. Various approximation methods have been developed to overcome these discontinuities (Neftci et al., 2019). One such method is based on the utilization of the rate-based approximations, a.k.a. the tuning curves. Given a loss function, the main idea is to build a network of differentiable rate-based approximation units and solve for the synaptic weights by using an arbitrary version of gradient descent. Once the solution is obtained, the approximation units can be substituted with LIF neurons to use the resulting spiking network during inference as shown in Figure 3. We utilized NengoDL Rasmussen (2018) to implement the aforementioned ANN to SNN conversion methodology. We employed the standard sparse categorical cross entropy as our loss function.

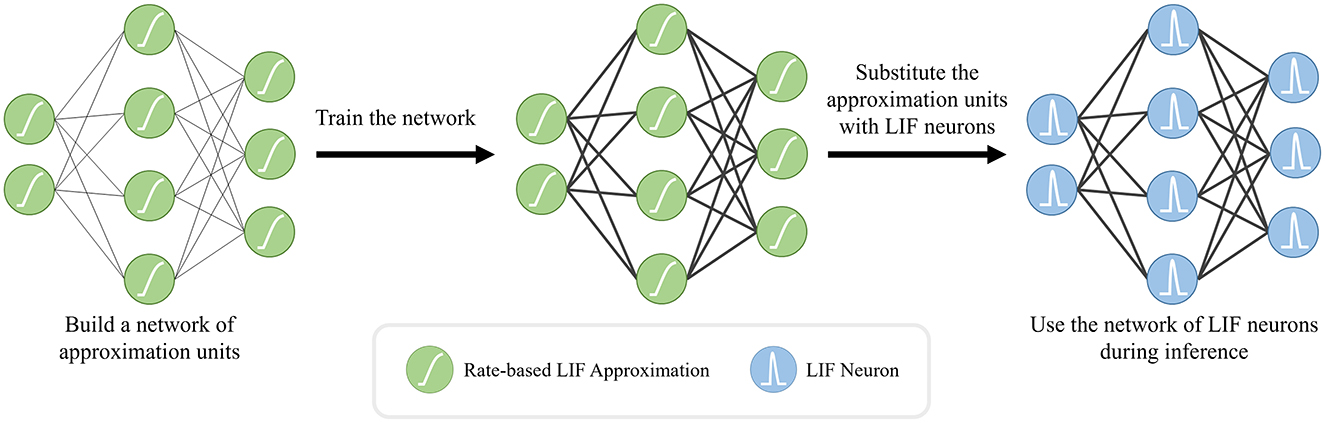
Figure 3. ANN-to-SNN conversion work-flow: we first employ rate-based approximations of the LIF neurons to train our network, since the discontinuous spike event outputs of the original LIF neurons prevents the training of the network through the back-propagation algorithm. After completing the training of this interim network, we substitute the LIF approximations with the original ones while keeping the network topology and the trained weights (bold black lines) the same.

3.3.3 LoCS-Net architecture

As depicted in Figure 4, LoCS-Net is composed of a sequence of 3 convolutional layers followed by a fully connected output layer, also known as the “place layer,” the units of which correspond to distinct places in the environment. Inputs to LoCS-Net are grayscale images of 56 × 56 pixels. The number of neurons in the place layer is set to be the number of possible places (NP) as explained in Section 3.2. We considered 50 × 50 grid for Oxford RobotCar (ORC) data in our principal experiments. Note that for training, we employ the smooth rate-based approximated LIF units while maintaining the same architecture illustrated in Figure 4. We use sparse categorical cross entropy as the loss function during training. For inference, we replace the approximated LIF units of the trained network with spiking LIF neurons, keeping both the weights and the architecture unchanged. For further details of the network structure and the corresponding hyper-parameters, we refer the readers to the supplementary information and to the repository of the current work's code at https://figshare.com/s/c159a8680a261ced28b2.

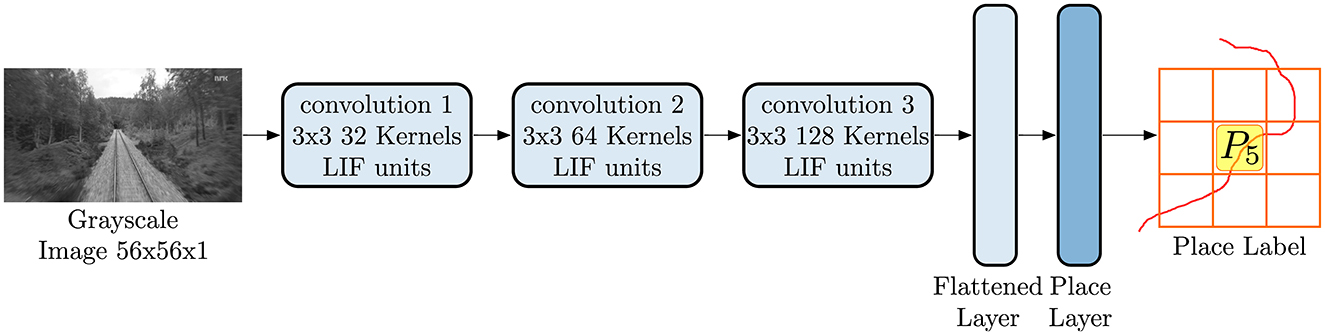
Figure 4. The LoCS-Net architecture consists of 3 convolutional layers followed by a fully connected output layer, known as the place layer. The units within this layer correspond to unique locations within the environment. LoCS-Net accepts 56 × 56 pixel grayscale images as inputs, using them to predict the associated places from which the input images were sampled.

4 Experiments 4.1 Datasets and evaluation metrics

We evaluate our proposed approach on the challenging Nordland (Olid et al., 2018) and ORC data (Maddern et al., 2017, 2020) following prior work (Hussaini et al., 2023). For the Nordland data experiments, we trained LoCS-Net using the spring and fall traverses and tested it with the summer traverse. For the ORC data experiments, we trained LoCS-Net on the sun (2015-08-12-15-04-18) and rain (2015-10-29-12-18-17) traverses, and tested its performance on the dusk (2014-11-21-16-07-03) traverse. We followed the Nordland data processing directions in Hussaini et al. (2023) for the same training and test data. We obtained 3,072 Nordland data (Olid et al., 2018) places, and 2,500 ORC data (Maddern et al., 2017, 2020) places (set by our grid definition) while considering the complete sun, rain, and dusk traverses used in Hussaini et al. (2023).

Although our discretization of the ORC domain yields a total of 2,500 possible places, the trajectories traversed in that dataset cover a much smaller number of labels. Some of the ORC data places are either occasionally visited or not visited at all. This is because the trajectories were generated by a vehicle traversing the road network, making it impossible to visit all parts of the spatial domain. Therefore, we filter out places that do not contain a minimum number (10) of unique training images. We also bound the number of unique instances per place from above (maximum 700) as the training of the baseline SNN models are getting infeasible due to increasing size of the data. Table 1 provides the training and the test data specifications yielded by our data pre-processing pipeline. We would like to note that LoCS-Net can still be trained and be tested on the full ORC data in a matter of minutes.

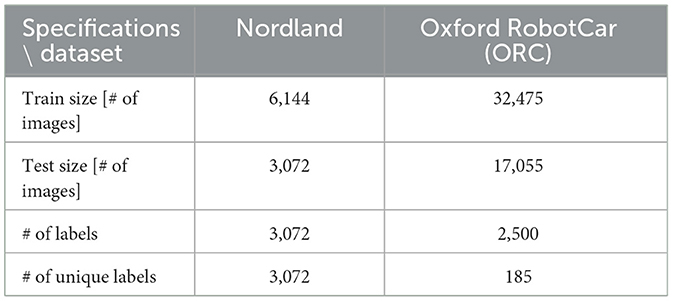
Table 1. LoCS-Net training and test data specifications.

We employ standard VPR performance metrics, including the precision-recall curves, area-under-the-precision-recall curves (AUC-PR or AUC) (Cieslewski and Scaramuzza, 2017; Camara and Přeučil, 2019), and recall-at-N (R@N) curves (Perronnin et al., 2010; Uy and Lee, 2018) in order to assess the performance of our model.

4.2 Experimental set-up

We adopt two annotation methods as the Nordland (Olid et al., 2018) and the ORC data (Maddern et al., 2017, 2020) were structured in different ways. Figure 5A describes the labeling process of the ORC images (Maddern et al., 2017, 2020). As it is shown, we first encapsulated the top-down projection of the path within a rectangular region. Then, we discretize this region to obtain grid tiles, each of which represents a distinct place. These tiles annotate the images sampled within its boundaries.

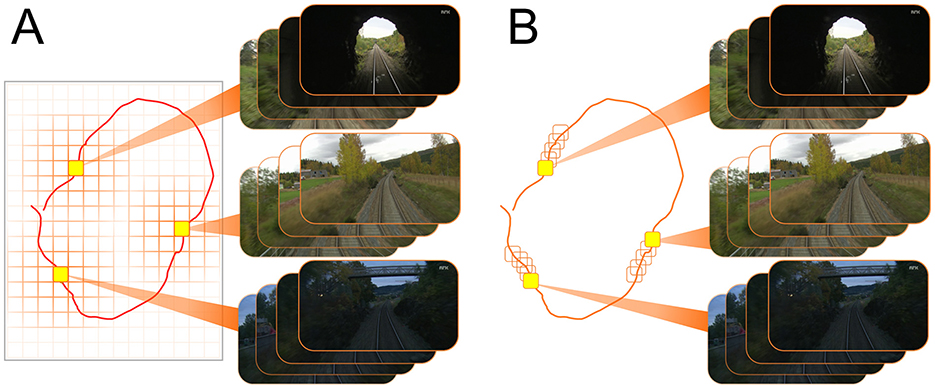
Figure 5. Annotating images: (A) top-down navigation domain is discretized by defining a grid of arbitrary resolution. Each tile of of the grid annotates the images sampled within its boundaries. (B) Images are sampled over a traverse at a pre-determined frequency while each image is corresponding to a unique place. For instance, if the first image is sampled at time t = 0s, then the second and the third image will be sampled at t = Ts and t = 2Ts, respectively.

To label the Nordland images (Olid et al., 2018) we followed the annotation method defined in Hussaini et al. (2023). As depicted in Figure 5B, we sample images over a traverse at a pre-determined frequency (every 8th image) while each image is corresponding to a unique place.

4.3 Quantitative results

We conducted several performance comparisons of LoCS-Net with the current SOTA SNN methods, Ensemble SNNs (Hussaini et al., 2023), VPRTempo (Hines et al., 2024), and Weighted Assignment SNN (WNA) (Hussaini et al., 2022). In order to save computational resources, we did not train and test WNA ourselves. Instead, in Table 2, we listed the performance metrics published in Table 1 of Hussaini et al. (2023). We also included additional performance comparisons of LoCS-Net to a set of ANN-based SOTA VPR techniques such as AP-GeM (Revaud et al., 2019), NetVLAD (Arandjelovic et al., 2016), MixVPR (Ali-Bey et al., 2023), Conv-AP (Ali-bey et al., 2022), EigenPlaces (Berton et al., 2023), and CosPlace (Berton et al., 2022). We utilized the benchmark tool developed by Berton et al. (2023) in order to perform these additional comparisons.

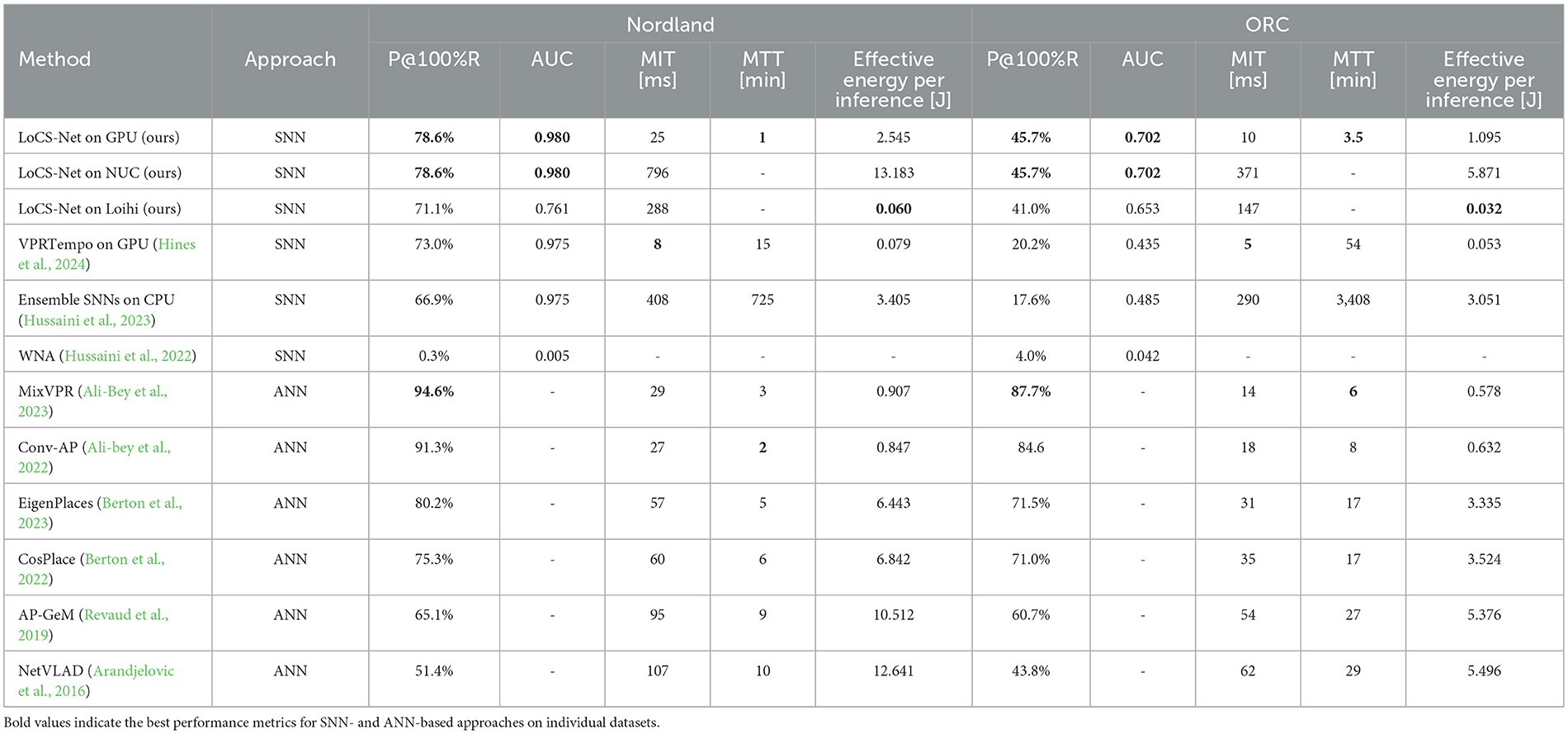
Table 2. VPR performance comparison in terms Precision at 100% Recall (P@100%R), area-under-the-precision-recall curves (AUC), mean inference time (MIT), mean training time (MIT), and effective energy consumed per inference.

Table 2 and Figure 6 summarize the VPR performance of LoCS-Net along with the reference methods. We observe that LoCS-Net outperformed all the SNN-based methods on both the Nordland (Olid et al., 2018) and ORC dataset (Maddern et al., 2017, 2020) by a large margin (78.6% and 45.7% respectively) in terms of P@100%R. LoCS-Net took much less time to train as reported in Table 2, which highlights LoCS-Net's compatibility for rapid prototyping and real-world deployment. Although it falls short of top-performing ANNs such as MixVPR and Conv-AP, LoCS-Net's strengths lie in energy efficiency and training time. While its GPU-based energy usage (2.545J) sits between that of ANNs like EigenPlaces (1.283J) and AP-GeM (5.376J), deploying LoCS-Net on neuromorphic hardware (Loihi) drastically reduces energy consumption, reaching just 0.032J per inference.

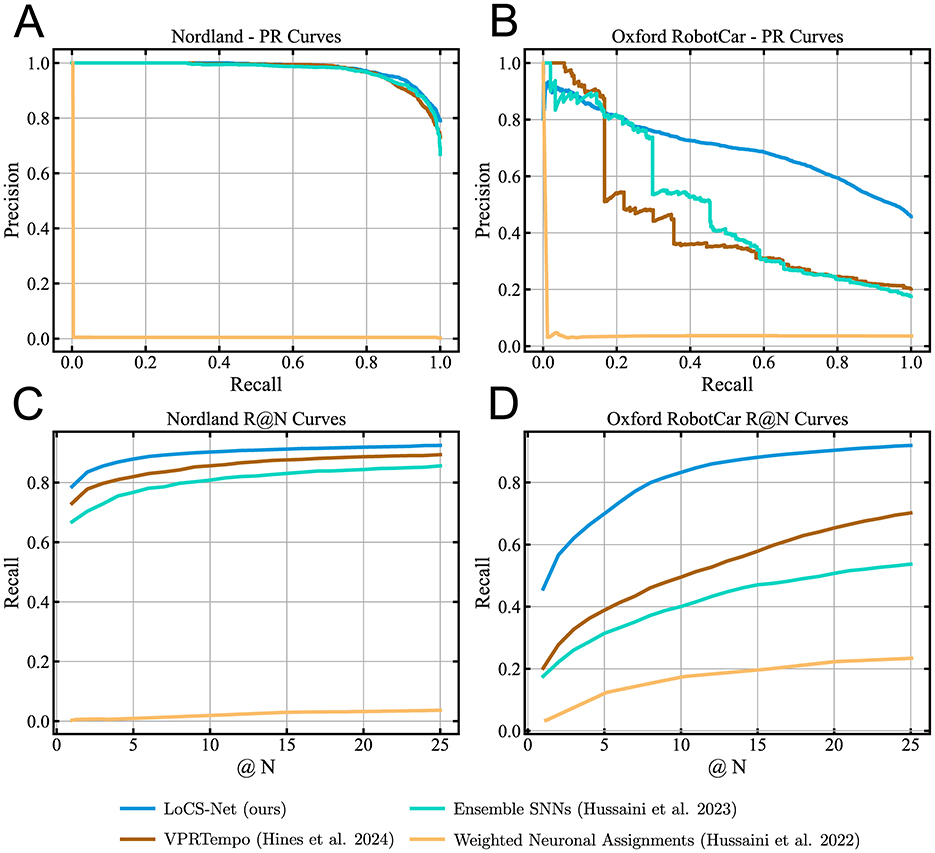
Figure 6. Precision-Recall and Recall @ N curves for the baseline SNN-based VPR methods and LoCS-Net: The blue, brown, cyan, and orange curves correspond to LoCS-Net, VPRTempo (Hines et al., 2024), Ensemble SNNs (Hussaini et al., 2023), and Weighted Neuronal Assignments (Hussaini et al., 2022), respectively. These figures demonstrate that LoCS-Net yields the best SNN-based VPR performance on both datasets. (A) PR curves obtained from the experiments on the Nordland dataset. (B) PR curves obtained from the experiments on the ORC datasets. (C) The R@N curves obtained from the experiments on the Nordland dataset. (D) The R@N curves obtained from the experiments on the ORC dataset.

Moreover, Figures 6C, D present the Recall @ N curves obtained from the evaluations of the methods on the Nordland (Olid et al., 2018) and ORC datasets (Maddern et al., 2017, 2020). LoCS-Net consistently yields the best Recall @ N performance compared to SNN methods on both datasets. These results indicate good scalability of the LoCS-Net model across thousands of locations, while maintaining computationally efficient inference, as illustrated by Table 2.

We conduct a sensitivity analysis of LoCS-Net with respect to the number of neurons used for signal representation, the maximum firing rate, and the synaptic smoothing factor. We note that the nominal LoCS-Net does not include synaptic filters in order to avoid the additional complexity imposed by temporal dynamics during training, as capturing precise synaptic dynamics is not our primary objective. Figure 7 presents the P@100%R sensitivity analysis of LoCS-Net on the Nordland Figure 7A and ORC Figure 7B datasets, focusing on the synaptic smoothing factor, maximum firing rate, and input layer resolution. All other neuronal and training parameters of the nominal LoCS-Net model remain unchanged. In Figures 7A, B, the synaptic smoothing sensitivity plots on the left use color-coded curves to represent different maximum firing rates for a nominal input resolution of 56 × 56. The middle plots isolate the effect of input resolution on model sensitivity, with dashed green curves showing the performance of the nominal LoCS-Net configuration. On the right, tables summarize the combined influence of the variances in synaptic smoothing factor and maximum firing rate, providing the same information as the left-hand plots. The P@100%R values of Figure 7 are computed as averages across simulations of five models initialized with different seeds per parameter set. The findings highlight that LoCS-Net is sensitive to variations in synaptic smoothing factor, maximum firing rate, and input layer resolution, with sensitivity being particularly evident on the Nordland dataset.

Figure 7. VPR performance in P@100%R sensitivity of LoCS-Net on Nordland (A) and ORC (B) datasets with respect to synaptic smoothing factor, maximum firing rate, and input layer resolution: The remaining neuronal and training parameters of the nominal LoCS-Net model (see Supplementary Tables S1, S2) are kept the same. Curves in the synaptic smoothing sensitivity plots (on the left) are color-coded, indicating model instances with different maximum firing rates with a nominal input resolution of 56 × 56. Plots in the middle depict the sensitivity with respect to only input resolution. Dashed green curves represent the performance of the nominal LoCS-Net model instance. Synaptic smoothing factor-maximum firing rate tables (on the right) illustrate the same data presented in the plots on the left. These tables contain the P@100%R values in white text while exhibiting the corresponding color codes at the same time. The P@100%R values are obtained by averaging the simulation results of five models, each initiated with a different seed for synaptic weights. The results suggest that LoCS-Net is sensitive to the synaptic smoothing factor, maximum firing rate, and input layer resolution, especially on Nordland data.

We further seek to understand the distribution of LoCS-Net's prediction errors on the ORC dataset. We quantify the prediction error in in terms of Manhattan Distance, as illustrated in Figure 8. 55.7% of the place predictions are within 1-Manhattan Distance of the ground truth labels. Yet, approximately 40% of the LoCS-Net place predictions fall beyond 5-Manhattan Distance of the ground truth labels. We did not perform the same analysis for Nordland data as it doesn't utilize a grid-based labeling structure as the Oxford RobotCar data.

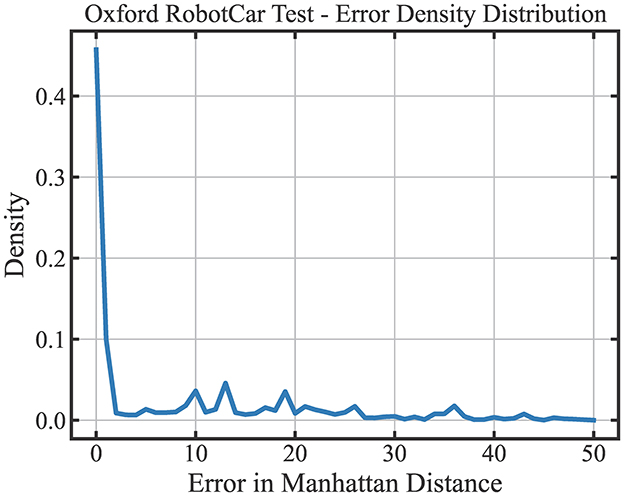
Figure 8. Prediction error distribution of LoCS-Net over the ORC dataset: 55.7% of the place predictions of LoCS-Net are within 1-Manhattan Distance of the ground truth labels. Approximately 40% of the LoCS-Net place predictions fall bey