. The K loss functions correspond to the K objectives to be optimized, and multiple objectives are merged into a single one by setting a scalarization weight for the objectives, as shown in Equation 25: L(θ)=∑i=1KωiLi(θ)    (25)

where ∑i=1Kωi=1, ωi ≥ 0, ∀i ∈ . Boundary constraints of ωi on ci are set as ωi ≥ ci, ∑i=1Kci≤1,ci ∈ [0, 1], ∀i ∈ .

To obtain Pareto efficient solutions, the aggregated objective loss function must be minimized, and the model parameters should satisfy the KKT (Chen, 2022) condition such that Equations 26, 27 are satisfied:

∑i=1Kωi=1,∃ωi≥ci,i∈    (26) ∑i=1Kωi∇θLi(θ)=0    (27)

where ∇θLi(θ) represents the gradient of Li. Considering the specific problem to be solved, we transform the KKT condition is as follows:

min.‖∑i=1Kωi∇θLi(θ)‖22s.t.∑i=1Kωi=1,ωi≥ci,∀i∈    (28)

A solution satisfying Equation 28 is a Pareto efficient solution. It has been demonstrated that these solutions result in gradient directions that minimize all loss functions (Sener and Koltun, 2018).

2.3.2.3 Framework of the algorithm

The framework begins with a uniform scalarization weight and proceeds by alternately updating the weights and model parameters. An optimizer is then utilized to ensure that the model converges effectively. As shown in Table 1 and Algorithm 1, the key part of the algorithm is to solve for conditionally generated weights for Pareto efficiency.

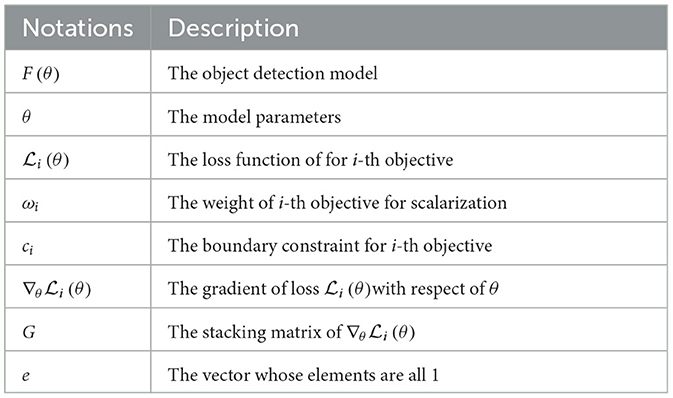
Table 1. Notations and description.

Algorithm 1. Dynamic hyperparameter tuning training method based on Pareto efficiency.

According to Equation 28, the problem is transformed into a quadratic programming algorithm by denoting ω^i as ωi − ci, and the Pareto efficiency condition becomes

min.‖∑i=1K(ω^i+ci)∇θLi(θ)‖22s.t.∑i=1Kω^i=1-∑i=1Kci    (29)

The Pareto efficiency condition is equivalent to Equation 29. However, addressing the issue at hand is not straightforward, given its quadratic programming structure. Initially, we opt to ease these limitations by focusing solely on the equation restrictions. Subsequently, we implement a projection technique that produces effective outcomes from the viable set that encompassed all restrictions. When all other constraints are omitted except for the equational constraints, as shown in Equation 30, the solution is given by Theorem 1.

min.‖∑i=1K(ω^i+ci)∇θLi(θ)‖22s.t.∑i=1Kω^i=1-∑i=1Kci    (30)

THEOREM 1. The solution to Equation 30 is ω^*=((M⊤M)-1Mz~)[1:K] where G ∈ RK×m is the stacking matrix of ∇θLi(θ), e ∈ RK is the vector whose elements are all 1, C ∈ RK is the concatenated vector of ci, and Z~∈RK is the concatenated vector of −GG⊤c and 1-∑i=1Kci and M=(GG⊤ee0).

During the solution process, the inverse operation of the matrix is negligible because the number of loss functions for object detection is small. However, the solution ω^* of Equation 30 may be invalid because the non-negative constraints are ignored. Therefore, we obtain an effective solution using the projection method, as shown in Equation 31:

min.‖ω~-ω^*‖22s.t.∑i=1Kω^i=1,ω~i≥0,∀i∈    (31)

Equation 31 represents a non-negative least squares problem, which can be easily solved using the active set method (Arnström and Axehill, 2021).

2.4 Summary

In the previous section, we presented three aspects of the improvement approach for unmanned object detection. First, we introduced an architecture to solve the insufficiency of the model for multi-scale object localization and detection. Subsequently, we developed a transformer encoder with group axial attention to reduce computation and enhance the inference speed. Finally, we presented a novel training technique that utilizes dynamic hyperparameter tuning inspired by the principle of Pareto efficiency. By dynamically adjusting the weights to align the training states of different loss functions, this approach effectively addresses issues related to manually assigning fixed weights. As a result, it enhances both the speed and accuracy of model convergence.

3 Experimental results and analysis 3.1 Setups 3.1.1 Dataset

Dataset 1 was selected from the COCO 2017 (Lin et al., 2014) dataset with category objectives related to autonomous driving, consisting of 10 categories, 35,784 images for training, and 2431 images for validation. Dataset 2 combines the original categories from the PASCAL VOC 2012 (Everingham et al., 2010) dataset, which include Person, Car, Train, Motorcycle, Bicycle, and Other, with 11,540 images for training and 2913 images for validation. Dataset 3 is sourced from the KITTI professional autonomous driving dataset (Geiger et al., 2013), primarily including categories such as Car, Pedestrian, Cyclist, Van, Truck, and Tram, with 7,481 images for training and 7,518 images for validation.

3.1.2 Evaluation metrics

The experimental evaluation metrics were AP, FPS, and GFLOPs. FPS and GFLOPs denote the inference speed and computation of the model, respectively. Specifically, APS and APM denote the AP for small- and medium-sized objects, respectively. AP is the area under the precision-recall (PR) curve, and precision (P) and recall (R) are calculated using Equations 32, 33:

where TP, FP, and FN denote the accurately recognized positive samples, erroneously recognized positive samples, and erroneously recognized negative samples, respectively. Mean average precision (mAP) can be computed by taking the average of the AP values across different categories, as illustrated in Equations 34, 35:

AP=∫01P(R)dR     (34) mAP=1n∑i=1nAPi    (35)

In the context of object detection, the average precision (AP) is calculated across different Intersection over Union (IoU) thresholds ranging from 0.5 to 0.95 with increments of 0.05. When the IoU threshold is specifically set at 0.5, it is denoted as AP50. The mAP is then computed as the average of the AP values for each category in the dataset. Therefore, all individual AP values mentioned correspond to the overall mAP.

3.1.3 Implementation details

The model was trained on an NVIDIA V100 GPU. In each stage the multi-scale feature and location information extraction method (MLEM), N was set to 3, 4, 6, and 3 correspondingly. The Adam optimizer was used for all experiments: initial_learning_ rate = 0.0005, weight_decay = 0.0001, and batchsize = 8.

3.2 Analysis of model parameters 3.2.1 Parameter analysis of multi-scale feature extraction module

To explore the effect of the scale n on this approach, n was set as a scale control parameter. Six experiments were designed with n = 1, 2, 3, 4, 5, 6. n = 1 represents a scale of one with no multi-scale fusion. Similarly, n = 2 represents a scale of 2, and the data are divided into two parts for multi-scale fusion. We adopted AP, APM, and APs as indicators, as shown in Figure 8.

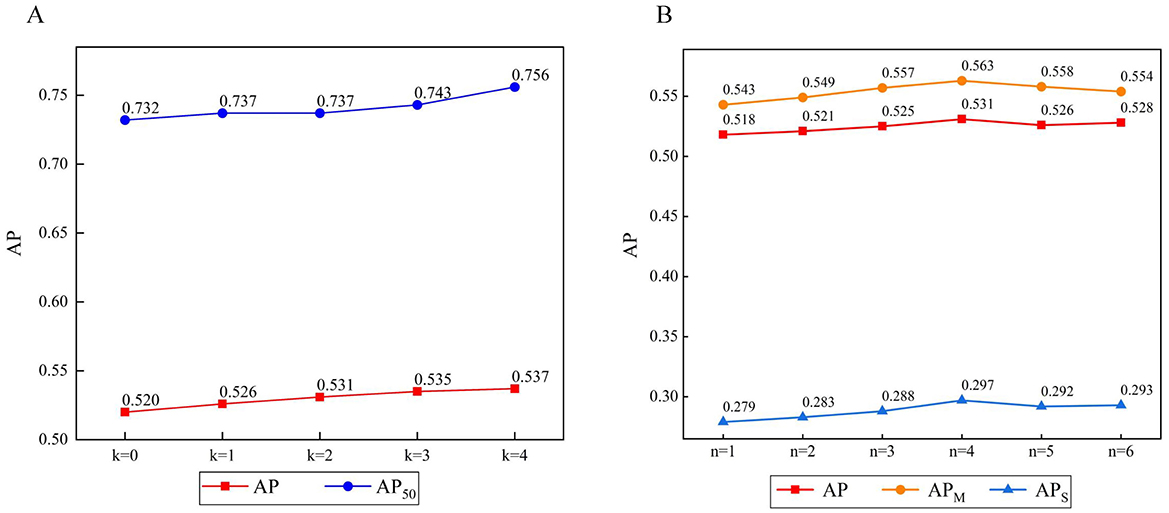
Figure 8. (A) The result of the number of CA modules. (B) The result of the number of scales.

The experimental results show that the multi-scale fusion operation has a significant effect on APS. An increase of n indicates that the number of different scales of the feature map fusion increases, and all show an upward trend. When n = 4, the multi-scale effect is obvious and optimal. When n = 5 or 6, the value of AP decreases slightly. Probably owing to limitations on the image size, the multi-scale feature extraction ability remains almost unchanged. However, an excessive number of branches can lead to a model degradation.

3.2.2 Parameter analysis of coordinate attention module

To investigate the effects of the CA module on the experiments, k was set as the experimental parameter. Five experiments were designed with k = 0, 1, 2, 3, 4. There are four stages: k = 0 denotes no use of CA, k = 1 denotes that the module is deployed in stage 1, k = 2 denotes that the module is deployed in the first two stages, etc. We adopted AP as an indicator, as shown in Figure 8.

The experimental results show that the CA module effectively improves the AP compared with the case of k = 0. Building on the multi-scale feature maps obtained in the previous stages helps further improve the effectiveness of CA in later stages. When k = 1 or 2, shallow features, such as space and details, are retained, which helps improve the AP. When k = 4, the enhancement effect of AP is weakened, but AP reaches its peak.

3.2.3 Parameter analysis of group axial attention layer

To investigate the effect of the attention range s on the feature map in the group axial attention layer, we set the number of encoders n = 6, the attention layer in the encoder adopts a single attention range for each encoder to the feature map, si denotes the i-th range combination, s0 denotes the original method, s1 = [1, 1, 1, 1, 1, 1], s2 = [2, 2, 2, 2, 2, 2], s3 = [1, 1, 1, 2, 2, 2], s4 = [1, 1, 2, 2, 4, 4], s5 = [1, 1, 2, 2, 6, 6], s6 = [2, 2, 4, 4, 6, 6], and we performed seven experiments, as shown in Figure 9.

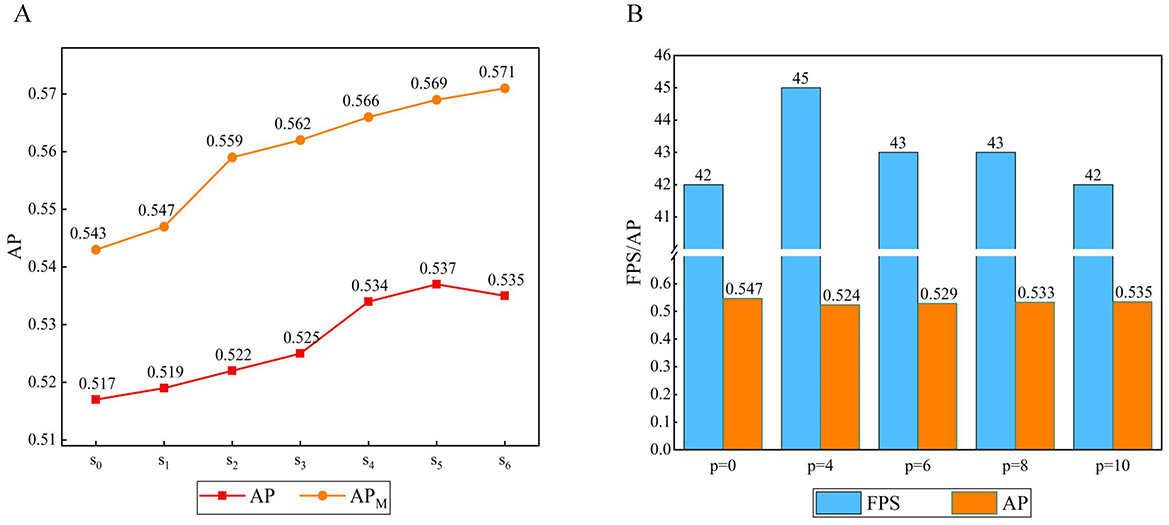
Figure 9. (A) Result of the range of group axial attention layer. (B) Result of the window size of window axial group attention.

When s0 becomes s1, the AP gradually increases. When the attention range is s2 the accuracy is further improved, probably due to the expansion of the attention calculation range. As the encoders continue to stack, the image feature level continuously increases. However, s1 and s2 do not take this case into account. From s3 to s6, the attention range increases. In the early stages, the smaller attention range facilitates learning of the local details of the image. In the later stages, a larger range is more conducive to learning the global information of the image. Therefore, s3 from to s5, APM is significantly improved compared to the cases of s1 and s2, and the AP reaches its best for s5. Comparing s6 and s1, it can be observed that a larger attention range is more favorable for targets at the medium scale.

3.2.4 Parameter analysis of window group axial attention

To explore the effect of window size on window group axial attention, we set the window size p as the experimental parameter, adjusted the size of the feature map to W = H in the encoder group axial attention layer, set the number of encoders to n = 6, and the attention range of the feature map in the group axial attention layer in each encoder was set to s5 = [1, 1, 2, 2, 6, 6], where p = 0 denotes no window partition, p = 1 denotes a partition size of 1 × 1, etc. Five experiments were conducted, as shown in Figure 9.

It follows that dividing the attention range within a fixed window can further reduce the computational complexity. When p = 4, the window size is smaller, the computation complexity is minimized, and the FPS increases; however, this will have a greater impact on dividing the attention region, which will lead to a lower AP. When p is larger, the impact on the operation of dividing the attention region is reduced, and although the individual window complexity increases, it leads to further increases in FPS and AP.

3.3 Ablations

Ablation experiments were conducted to evaluate the effectiveness of the proposed method. We trained our model on the COCO dataset and ensured that the experimental conditions were consistent. Exp. 1 represents the baseline, based on which we adopted the MLEM the transformer encoder based on the group axial attention mechanism (TEGA), and dynamic hyperparameter tuning training method based on Pareto efficiency (DHMP). A total of eight ablation experiments were performed, as shown in Table 2. Exp. 2 shows that the addition of MLEM resulted in a 1.6% increase in AP over DETR, demonstrating that multi-scale features have a more significant impact on the results. Exp. 3 shows that after adding TEGA, AP is improved by 0.9% compared to DETR, and compared to MLEM, the improvement is minimal, which indicates that the accuracy of the detection may depend on the pre-processing of the features; however, other experiments demonstrated that encoders have a material impact in terms of reducing model complexity and increasing inference speed. Exp. 3 shows that adding DHMP can make the model converge with a higher accuracy. A comparison of the results of Exps. 5–7 with those of Exp. 8, respectively, shows that each improvement is necessary to improve detection. Exp. 8 shows that applying all three improvements simultaneously significantly improves the accuracy, with a 2.4% improvement in AP.

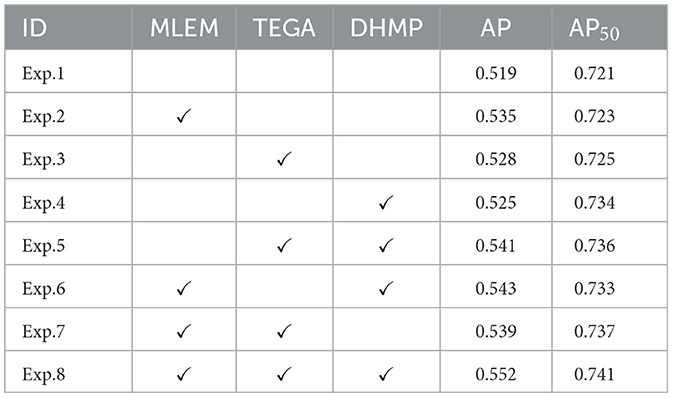
Table 2. Ablation experiments number and results.

As shown in Table 3, we conducted several groups of ablation experiments to demonstrate the effectiveness of Window G-Attention (WGA). Dataset 1 and Dataset 2 represent the COCO and PASCAL VOC datasets, respectively. Exp. 1 refers to the improved method without using WGA. By comparing the results of Exps. 1 and 3, as well as Exps. 2 and 3, we conclude that WGA contributes to improving FPS. It is worth noting that the degree of FPS improvement achieved by WGA varies across different datasets, which we believe is related to the distribution of objects within the images. In addition, we observed that the smaller the window size p of WGA, the lower the computational complexity and the higher the FPS, which is consistent with the conclusion we reached in the article.

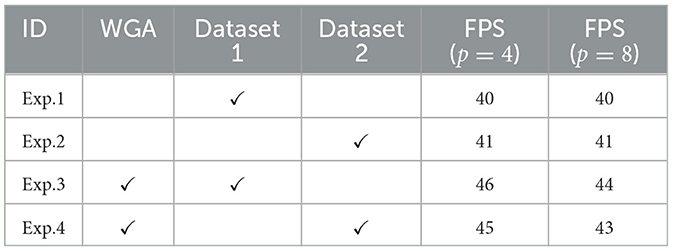
Table 3. Ablation experiments number and results.

Figure 10 reflects the accuracy trends before and after the improvement in the algorithm. The original method still has no convergence trend over 50 epochs, the AP and AP50 increase slowly, and the accuracy only reaches approximately 50% that of our method after 25 epochs, and the accuracy only reaches approximately 5% that of our method after 25 epochs. The accuracy of our method increased faster in the early stages of training, with AP and AP50 reaching 0.535 and 0.735, respectively, at epoch 20, which was higher than the accuracy of DETR at epoch 50. After 25 epochs, our method converges, indicating that DLMP is effective, and AP and AP50 finally reach 0.552 and 0.743, respectively.

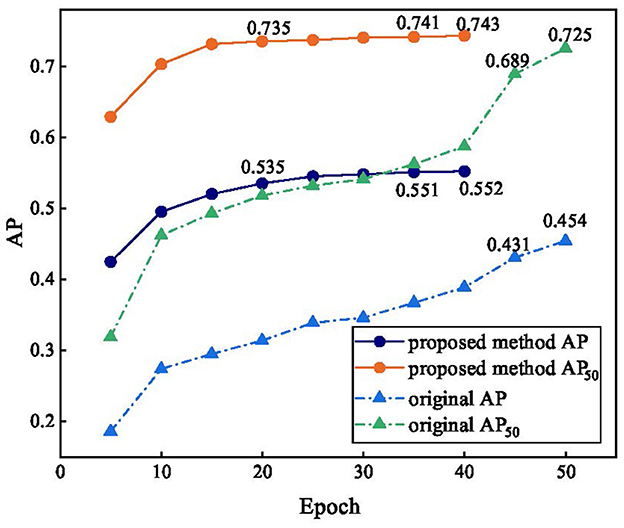
Figure 10. Comparison of accuracy trends before and after improvement.

3.4 Comparison with other methods

In this section, we compare our method with current mainstream algorithms on the COCO, PASCAL VOC and KITTI datasets, as shown in Tables 4–6. As shown in Table 4, the AP of our method is 0.552, and its AP50 is 0.741; both are the best, although APS is 1.4% lower than that of YOLOv8, and the actual epochs required for training are less than for YOLOv8. Compared with DN-Deformable-DETR and DINO-DETR, the proposed method maintains APS at the same level as the former and 0.4% higher than the latter while significantly reducing the GFLOPS and params. Compared to DETR, our method reduces the number of parameters by approximately 10% and improves the AP, AP50, and APS by 3.3%, 2.1%, and 4.5%, respectively, which is advantageous for DETR-like models.

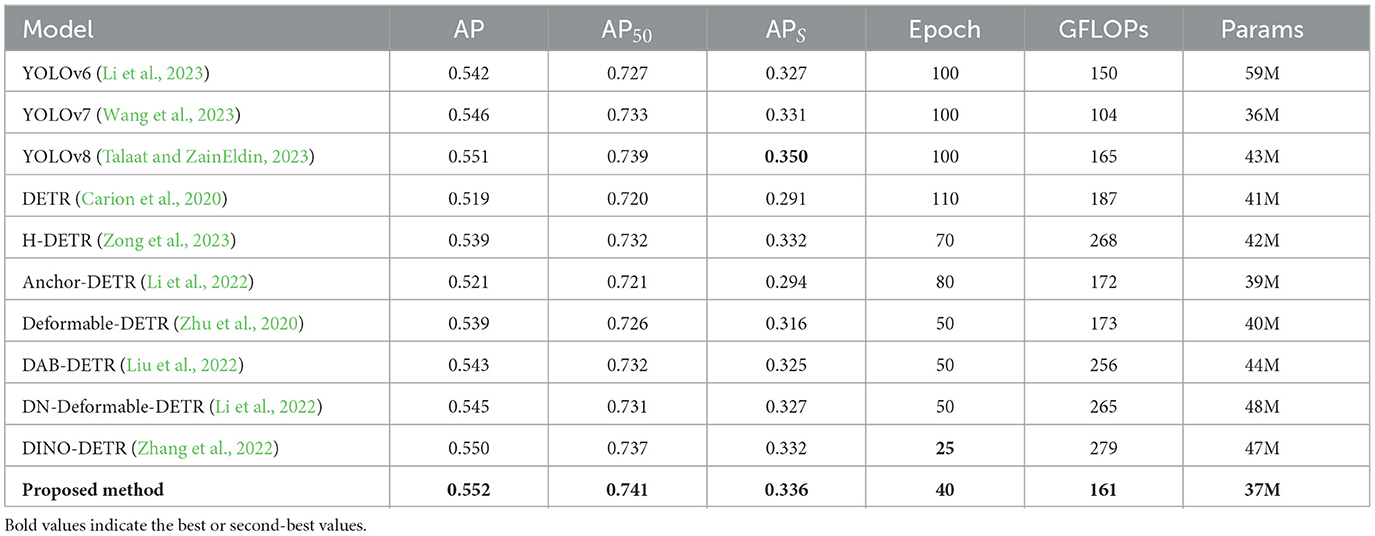
Table 4. The results of comparison.

Table 5 shows the experimental results of the different methods on PASCAL VOC. The AP of our method is 0.477, which is only lower than that of YOLOv8. The proposed method reaches convergence in 35 epochs, which is only higher than that of DINO-DETR, showing good convergence speed and more satisfactory detection accuracy.

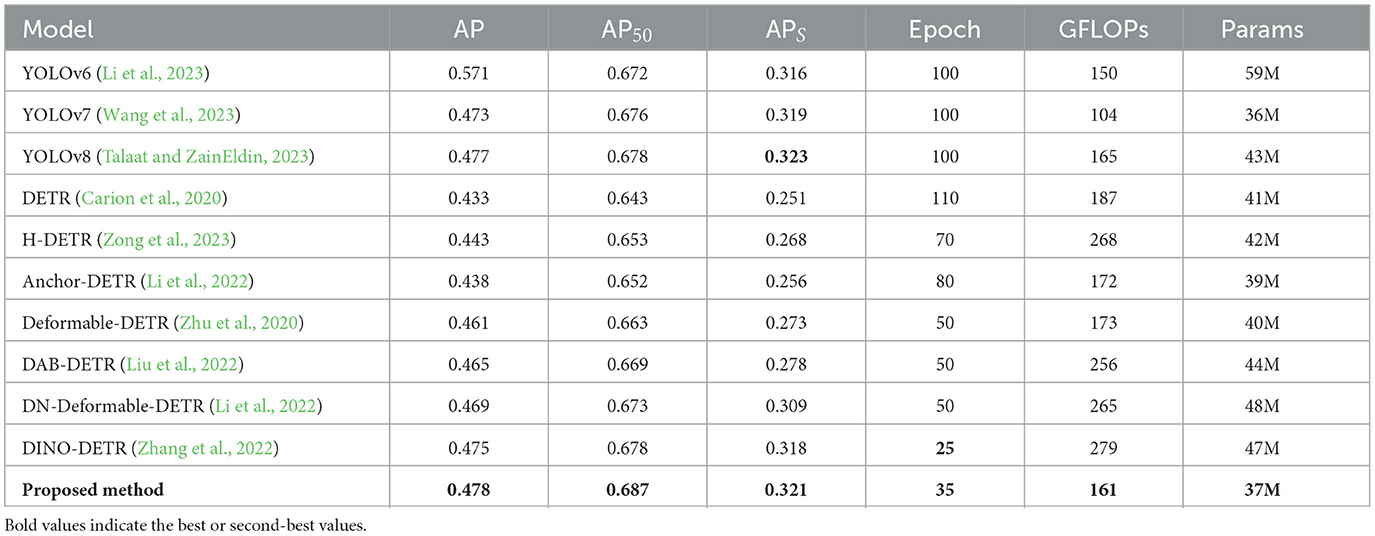
Table 5. The results of comparison.

Table 6 shows the results of different methods on the KITTI dataset. Our proposed method achieves the highest AP value of 0.556, representing a 3% improvement compared to the baseline method. Our method converges within 35 epochs, second only to DINO-DETR. In terms of APS evaluation, our method is only slightly behind YOLOv8 and is nearly on par with it, while having fewer model parameters and lower computational complexity.

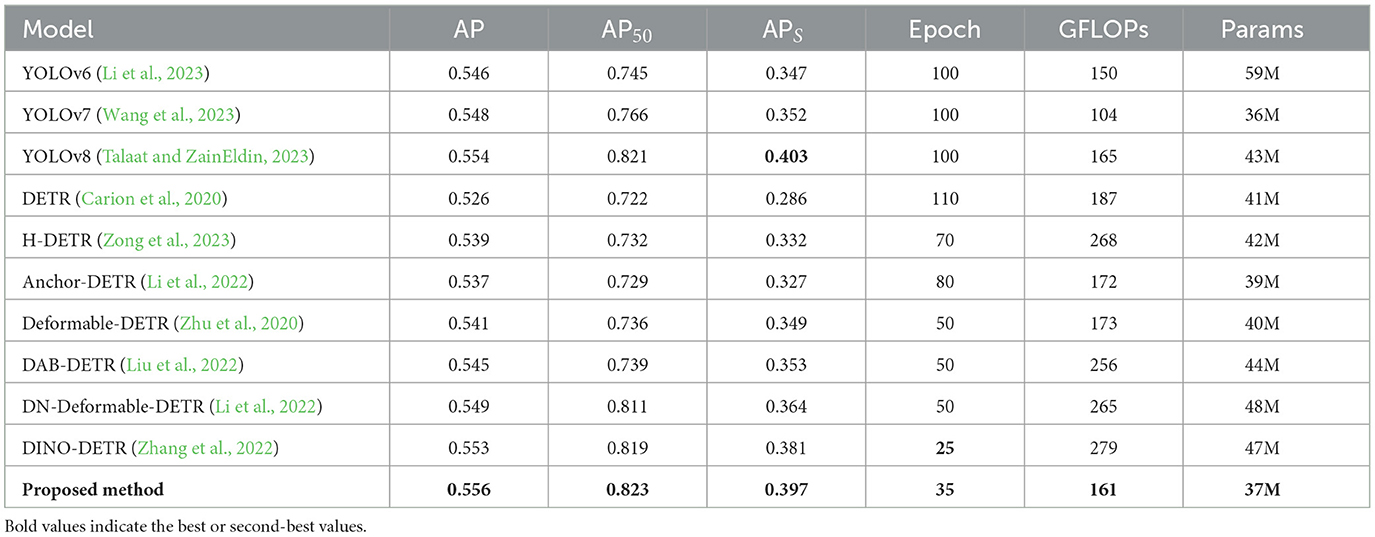
Table 6. The results of comparison.

The convergence of the different algorithms during training is shown in Figure 11. The training of the proposed method essentially converged in fewer than 45 epochs, which is a remarkable improvement over DETR and YOLOv8. DINO-DETR converges in the 25th epoch, but in actual training, owing to its high complexity, the actual training of an epoch is approximately three times as long as that of the proposed method.

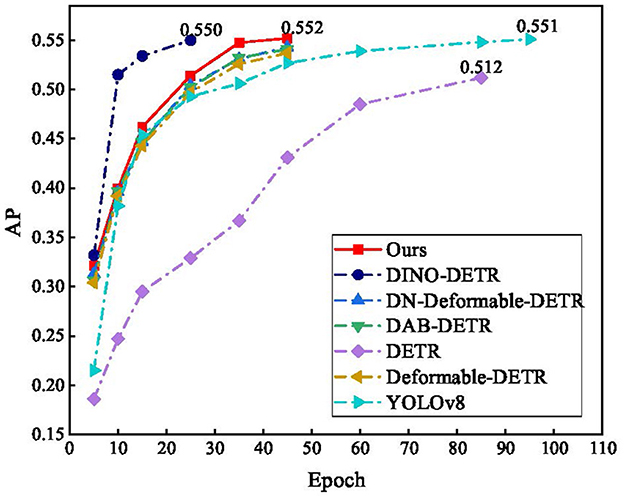
Figure 11. Results of comparison.

Figure 12 shows the relationship between the model computation GFLOPs and FPS and test images from the COCO and PASCAL VOC datasets, with an image size of 900 × 900. The proposed method had the smallest GFLOPs and best FPS in the DETR series. Version v1 uses Window G-Attention, and there is still a large gap in the FPS compared to YOLOv8; however, the FPS is improved by 84% compared to DETR.

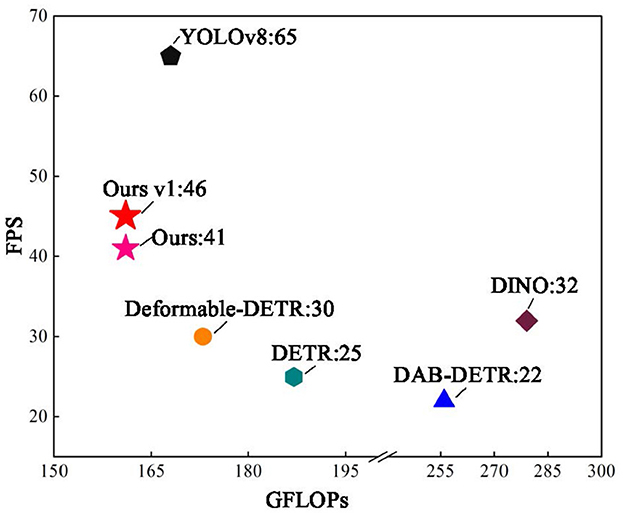
Figure 12. Comparison of FPS with different algorithms.

In conclusion, the proposed method demonstrates robust performance across three distinct datasets. First, the AP values underscore the superior detection accuracy of the method, effectively identifying objects of varying scales in autonomous driving scenarios, including obstacles, vehicles, pedestrians, and traffic lights. Second, considering the inherent constraints of computational resources and energy consumption in autonomous driving hardware, our model is designed to minimize parameter size while achieving notable computational efficiency compared to mainstream object detection algorithms. With respect to the FPS metric, our method achieves the best performance among DETR-based algorithms, satisfying the stringent real-time detection requirements of autonomous driving systems. Furthermore, the proposed model is implemented using the PyTorch framework, ensuring seamless deployment on vehicle-embedded hardware. Notably, our method exhibits slightly lower performance on the APS metric compared to YOLOv8, likely due to the embedded data augmentation techniques employed by YOLOv8. This insight highlights a promising direction for further optimization and refinement of our algorithm.

3.5 Visualization

We tested the visualization of the different methods in various driving scenarios. The threshold for each detector was set to 0.6, and the performances are shown in Figures 13–15. Each image shows visualization of several approaches (Corresponding order from top to bottom, left to right): (a) the image to be detected, (b) DETR, (c) Deformable-DETR, (d) DAB-DETR, (e) DN-Deformable-DETR, (g) DINO-DETR (f) YOLOv8, and (h) the proposed method. According to the experimental results, the proposed method addresses the issues of omission and false detection caused by mutual occlusion, mutilation, and the small size of the target, and it has excellent adaptability to complex scenes.

Figure 13. Visualization of the proposed method compared with current methods in suburban road scenes.

Figure 13 shows a suburban road scene with clearer vehicle targets, but the problem of missing the car occurs in both (b) and (c), where the person in the car is a more difficult target to identify, and the remaining methods did not produce a missed detection. Both the proposed method and YOLOv8 detected traffic signs and the farthest vehicle.

Figure 14 shows a street scene, where people stand densely and the