Cross-sectional studies of the human microbiome have identified a wide range of outcomes and exposures associated with the human microbiome ranging from type 2 diabetes (Qin et al., 2012; Larsen et al., 2010) to colorectal cancer (Zackular et al., 2014; Feng et al., 2015). These findings have shed light on the biological mechanisms underlying many conditions and provided critical clues as to novel therapeutic and risk reduction interventions, but a serious weakness of many of these classical studies is the limited information on how the microbiome changes over time and how these changes may affect outcomes. This has motivated the development of longitudinal microbiome studies where specimens are collected and profiled over a period of time. These studies promise comprehensive opportunities to gain better insight into topics such as how the microbiome varies over the course of a treatment (Lawrence et al., 2014; Jackson et al., 2016) and how the microbiome may sit within the causal pathway of some conditions (Turnbaugh et al., 2006; Wang et al., 2018), among many other opportunities. However, despite the potential and promises, serious analytical challenges persist.

Visualization is a particular challenge in longitudinal microbiome studies, yet it represents an important and standard step in most microbiome data analysis workflows. As in the analysis of other omics data types, visualization allows for the assessment of outlying samples and quality control. However, within the context of microbiome studies, it takes on an additional role by allowing for an understanding of microbial community structures in relation to metadata. The most popular approach for visualizing microbiome data is through Principal Coordinates Analysis (PCoA) (Gower, 2014) in which individual samples are plotted on a scatter plot. Like classical principal component analysis (PCA), the coordinates of each sample are determined based on capturing the greatest variability in the data, but whereas PCA focuses on linear transformations, PCoA allows for better capture of nonlinear transformations. Operationally, PCoA is performed by calculating a matrix of pair-wise dissimilarity between samples, where the dissimilarity measure is thought to be ecologically relevant and captures certain aspects of community structure (e.g., phylogeny, presence/absence, and abundance of taxa, etc.). The dissimilarity matrix is then transformed to a matrix of pair-wise similarity through Gower centering, and the principal coordinates are calculated as the eigenvectors of the similarity matrix. Such analyses have enabled a better understanding of many conditions and even the discovery of possible enterotypes (clusters) (The Human Microbiome Project Consortium, 2012; Arumugam et al., 2011).

In longitudinal microbiome studies, PCoA could provide information on how community structures change over time and how these changes correlate with variables of interest. However, guidance on how to carry out PCoA in longitudinal studies including multiple samples from the same subjects is lacking. PCoA strategies for repeated measures, such as in longitudinal studies, face additional challenges due to the inherent correlation between repeated observations from the same subjects. Currently, data across all subjects and time points are amalgamated, and plots are generated in the same way as in cross-sectional studies. This approach, however, may not be suitable when the goal is to analyze the temporal dynamics or subject-specific effects.

In longitudinal studies, factors such as subject clustering, irrelevant variables, and time effects often dominate the variability, overshadowing structures related to the variables of interest. Applying PCoA without adjustments for repeated measures may obscure important temporal patterns or subject-level effects, as the method assumes that all samples are independent. For example, high correlation between samples from the same subject can distort shifts over time or distort relationships with other variables.

How to accommodate these obfuscating effects in longitudinal analysis remains unclear. Our proposed method accounts for repeated measures by incorporating random effects and covariates to model within-subject correlations. This approach yields more accurate visualizations of temporal changes and effects of interest, ensuring that the primary sources of variability reflect the variables of interest rather than confounding factors.

For longitudinal microbiome studies, we propose a strategy to mitigate the effects of variables and data characteristics that may obscure the primary structures of interest in PCoA plots. This approach is also applicable to other repeated measures study designs, such as clustered microbiome measurements from individuals sharing households. Therefore, throughout this discussion, we will refer to repeated measures designs more broadly. Our proposed framework involves removing the confounding effects from the pair-wise similarity matrix while accommodating the repeated-measure nature of the data. Our framework is similar to covariate-adjusted PCoA (Shi et al., 2020), which is used for cross-sectional studies, but it also accounts for correlation among observations by incorporating random effects in a linear mixed model (LMM). Specifically, we estimate the similarity matrix, adjust out potential obfuscating effects from each PC of the similarity matrix using LMMs, and reconstruct the similarity matrix for usual PCoA analysis using the residuals from the LMM. Since there are multiple notions of residuals in LMMs (Verbeke et al., 1997), we consider multiple concepts of residuals (including marginal and standardized residuals) and provide guidance on their recommended use.

We find that our approach effectively distills the most important axes of microbiome community variation while reducing the influence of nuisance covariates in our visualizations, all while leveraging shared information across distinct time points. However, we also found that relying on marginal or conditional residuals from LMMs can be inadequate for certain analytic objectives, as unwanted structures may persist. This persistence is due to dependencies introduced by the replacement of parameters with their estimates, a challenge that is particularly pronounced in dependent data (Wakefield, 2013). To overcome these challenges, we further recommend standardization of residuals as an essential step to mitigate dependencies when the dependencies are not of primary interest. Collectively, we find that our approach and recommendations offer the ability to facilitate understanding of shifts in community structure in relation to time or other variables of interest.

In the following sections, we first review PCoA before describing our proposed strategies for adjusting out uninteresting effects. We then apply our approach within simulated examples to illustrate the potential utility and to offer specific guidance. Finally, we demonstrate the utility of our approach in two real data sets before concluding with a brief discussion.

PCoA begins by constructing a matrix of pair-wise dissimilarities between each pair of samples, D, where the (i,i′)th element of D is the dissimilarity between samples i and i′. A wide range of, typically nonlinear and ecologically relevant, dissimilarities are commonly used within the microbiome analysis literature. Each dissimilarity emphasizes different aspects of the data and captures different qualities of the community structure. For example, Bray-Curtis dissimilarity (Roger Bray and Curtis, 1957) emphasizes relative abundance such that more common taxa tend to drive dissimilarity. On the other hand, UniFrac distance (Lozupone and Knight, 2005) focuses on dissimilarity based on the presence/absence of taxa such that rarer taxa can exert greater influence, and further incorporates phylogenetic relationships among taxa when estimating distance. Extensions of UniFrac, such as weighted UniFrac (Lozupone et al., 2007) and generalized UniFrac (Chen et al., 2012), focus on more common taxa or compromise between rare and common taxa, respectively, while still accommodating phylogeny. Other distances such as Aitchison distance (Aitchison, 1982) try to respect compositional effects. The choice of distance is based on the type of relationships that investigators seek to study or believe to be relevant.

After calculation of D, the distance is transformed to an n×n similarity matrix which we denote K via Gower centering:

where H=1(1′1)−11′. The principal coordinates (PCs) are computed as the eigenvectors of K, and the proportion of variability in the nonlinear space explained by each PC is given by the relative magnitude of the corresponding eigenvalue.

The PCs represent lower-dimensional embeddings of the data. For visualization, the top PCs are plotted against each other to generate PCoA plots. Specifically, the PCoA plot is a scatter plot where each point corresponds to a separate sample, and the coordinates of each point (sample) are determined by the value of the PCs. In practice, only the top few (sometimes only the top two) PCs are used for visualization, even though the proportion of variability explained may be modest.

A limitation of PCoA is that the PC directions can be driven by confounding variables, denoted X, which leads to the obfuscation of structures of primary interest, i.e., related to a variable of primary interest. Thus, adjusted PCoA (aPCoA) (Shi et al., 2020) was developed to address this by essentially regressing out the effect of obscuring variables. Specifically, the covariate adjusted similarity matrix is calculated as

Essentially, one is re-centering K based on the covariates.

One way of justifying this approach is the following. We first calculate the matrix K as before and then decompose K=ΦΦ′ where Φ=[Φ(1),…,Φ(n)]=K is a matrix square root. A natural choice of decomposition is to set Φ=UΛ1/2 where UΛU′ is the eigendecomposition of K. The Φ(k)’s (the columns of Φ) are simply the original PCs. Then aPCoA essentially regresses each PC on X and calculates the residual (i.e., corrected PCs). The matrix of residuals is E with kth column given as

By regressing out the effect of the covariates X, each E(k) is now orthogonal to the covariates. Then the covariate-adjusted similarity matrix can be recalculated as K*=EE′ — note that one cannot simply use E as the PC since proportions of variability explained have shifted. At this point, PCoA proceeds as before, just using K* instead of K. This gives the same result as in Equation 1.

Importantly, however, although aPCoA is useful for removing covariate effects, it cannot directly handle repeated measures designs. This approach assumes that each sample is independent, which is not the case for repeated measures data. In such data, samples taken from the same subject over time are correlated, and failing to account for this correlation can result in misleading visualizations where the effects of repeated measures dominate the patterns of interest.

In contrast, our method, detailed in the following section, extends traditional aPCoA by incorporating linear mixed models (LMMs) that account for both fixed effects (e.g., treatment, age) and random effects (e.g., subject-level variability) to properly adjust for the repeated measures structure. By adjusting for within-subject correlations, this method ensures that temporal changes in microbiome profiles are more accurately captured, and that variability due to repeated measures does not obscure key patterns related to covariates or treatment effects.

As earlier, the goal is to adjust Y in such a way that we can meaningfully plot patterns embedded in the data. The general strategy follows a similar approach to aPCoA but includes some key differences. First, to accommodate the repeated measures and longitudinal sampling, we incorporate linear mixed models into the calculation of residuals in Equation 2. Second, because of using mixed models, the convenient formulas in Equation 1 are no longer usable in the repeated measures setting, which requires more explicit correction. Finally, there is no unique concept of “residual” for linear mixed models (Verbeke et al., 1997). With multiple notions of residual, the choice of which one to use depends on the context and analytic objective, but we suggest the use of standardized residuals in general.

With these considerations in mind, we propose the following steps for our method, which are also illustrated in the workflow in Figure 1. Before applying it, we recommend normalizing the microbiome data to account for differences in library sizes across samples. Specifically, we suggest using the centered log-ratio (CLR) transformation on relative abundances in conjunction with the Aitchison kernel matrix. By expressing each feature as a log-ratio relative to the geometric mean of all relative abundances in a sample, CLR reduces the influence of total sequencing depth, making the data more comparable across samples. Additionally, CLR-transformed data are more amenable to linear transformations, which makes them particularly well-suited for methods that rely on linear modeling, such as our approach. The Aitchison kernel is ideal for compositional microbiome data, as it respects the relative nature of the data and ensures that variations in sequencing depth do not bias the results. Throughout the rest of the text, we use the Aitchison kernel for these reasons. However, if an alternative kernel matrix, such as Bray-Curtis, is needed, then relative abundance data may be more appropriate, as CLR-transformed data are not suitable for such distance measures. Therefore, users should choose between raw count, relative abundance, or CLR-transformed data based on the kernel matrix and specific analysis objectives, with the Aitchison kernel being the preferred choice for compositional data.

1. Kernel Construction: Embed microbiome data Y into an appropriate kernel (similarity) matrix K, as usual. Throughout the text, we use Aitchison kernel matrices because they are well-suited for compositional data like microbiome datasets. Specifically, Aitchison distance accounts for the relative nature of the data and is compatible with CLR-transformed data. As in earlier steps, we calculate an ecologically relevant distance between all pairs of samples, which may no longer correspond to unique individuals, and Gower-center this distance matrix to form the kernel matrix, as is typical in PCoA.

2. Kernel PCA: We then obtain kernel PCs, K=UΛ1/2, from K=UΛU′ using all samples and without regard to the repeated measures sampling, as before.

3. Retain Key Kernel PCs: Retain the top ℓ≤rankK kernel PCs that explain a large proportion of the variability in K. Possible choices for proportion of variability explained could be 90% or 95%.

4. Covariate Adjustment: Regress kernel PC r, r=, on any “nuisance” covariates as fixed effects (e.g., age, sex, study site) and/or random effects (e.g., random slopes for time within subject/cluster), as well as random intercepts for subjects/clusters to account for repeated measurement. For subject i, given fixed effect vector xi and random effect vector zi,

where β(r) is the vector of fixed effect coefficients, γi(r) is the vector of random effect coefficients for the ith subject/cluster, and ϵi(r) is the vector of residual errors.

5. Standardize Residuals: Obtain estimated standardized residuals ê*(r). To do so, first, obtain marginal (population-level) residuals, ei(r)=Φi(r)−xiβ̂(r). If Vi is the true error structure, then varei(r)=Vi, and varêi(r)≈V̂i. The dependence within our residuals may affect visualization of the data. Therefore, we standardize to remove the dependence within the residuals. Next, we let V̂i=LiLi′ be the Cholesky decomposition of V̂i. Then, we can form estimated standardized residuals

Now, varêi∗(r)≈I.

6. PCoA on Reconstructed Adjusted Kernel Matrix: Then as in aPCoA, we reconstruct the adjusted kernel matrix K*, from which we can perform usual PCoA. For completeness, this proceeds by calculating the eigendecomposition of K*=(U*)Λ*(U*)′. The PCs are then the columns of K*=U*(Λ*)1/2.

7. Visualize: The top PCs, or first few columns, of K* can be plotted against each other. The proportion of residual variability explained is given by the relative magnitude of the diagonal values of Λ*.

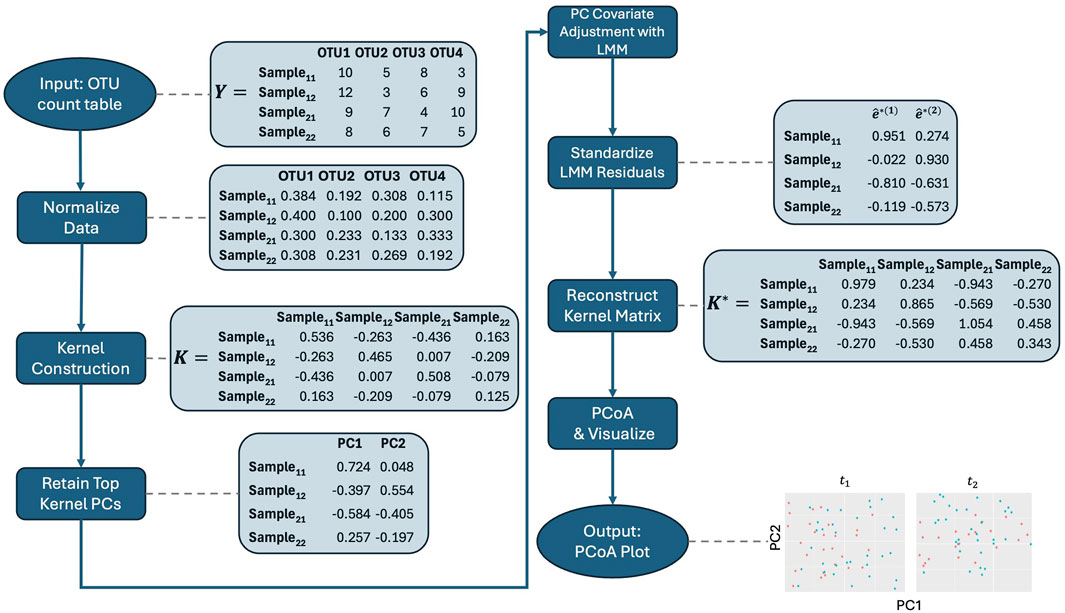
Figure 1. Workflow for the adjusted PCoA method applied to repeated measures microbiome data. The process starts with data normalization, followed by kernel construction. Kernel principal coordinates are extracted and adjusted for covariates using linear mixed models. The residuals are standardized, and the adjusted kernel matrix is reconstructed before visualizing the top principal coordinates using PCoA. Note that the data shown are illustrative and do not directly lead to the final plot displayed in the figure.

Note that in Step 3, we drop a few of the PCs that explain very small proportions of the variability. This step is not theoretically necessary but is important in practice as the low variability of the tail eigenvectors leads to difficulties in fitting the mixed models. Due to the low percentage of variability explained, their removal typically does not affect the overall visualization.

For supplementary analyses comparing the proposed kernel-based aPCoA and aPCoA on CLR-transformed data, please refer to the Supplementary Material.

We compared the proposed method described in Section 2.2 to the aPCoA method for cross-sectional studies, as outlined in Section 2.1, and to an approach where we only adjusted for sex as a fixed effect.

For the aPCoA approach, we first stratified all data points by time. Within each stratum, we embedded the simulated microbial counts into an Aitchison distance, generated a kernel matrix, and obtained the kernel PCs. We then regressed each kernel PC on sex in a linear model, computed the residuals, and derived the PCs from the resulting residuals matrix. Finally, we plotted PC2 against PC1 for each time point.

For the fixed-effect-only approach, we embedded all simulated microbial counts Y into an Aitchison distance, generated a kernel matrix K, and obtained the kernel PCs. We then regressed each kernel PC on sex in a linear model, computed the residuals, and derived the PCs from the resulting residuals matrix. Finally, we plotted PC2 against PC1 for each time point.

For the proposed aPCoA approach for repeated measures, we embedded the simulated microbial counts Y into an Aitchison distance, which was used to generate a kernel matrix K. We then obtained the kernel PCs (Φ) from K and retained the top ℓ=69 kernel PCs, which explained approximately 90.1% of the variability in K. Each of the ℓ kernel PCs was regressed on sex, time, and their interaction as fixed effects, and a random intercept for each subject, using a linear mixed model. The estimated standardized residuals were then computed, an adjusted kernel matrix was constructed, and the PCs of the adjusted kernel matrix were obtained. Finally, we plotted PC2 against PC1 for each time point.

For this scenario, we simulated data on n=100 subjects at m=4 time points, following a similar approach to that described in Section 2.3.1. We initialized data at t0 the same as in the previous section. Sickness status was simulated as a time-varying binary covariate, following a standard Bernoulli distribution independently across time points. For subjects who were sick at t0, we multiplied the counts of 20 randomly selected sickness-affected taxa by 24.

For subsequent time points, tj, j∈, we initialized taxa counts as in Section 2.3.1; generated shared changes in the community profiles across all subjects by multiplying the counts of 20 randomly chosen taxa by 0.25; generated a treatment effect by multiplying the counts of 20 randomly selected taxa by 3; and finally generated a sickness effect by multiplying the counts of the differentially prevalent taxa (described in the previous section) by 24. None of the taxa sets overlap, and we used the same taxa sets across all time points. After counts at all time points were generated, we rounded all taxa counts to the nearest whole number.

We compared the proposed method described in Section 2.2 to the aPCoA method for cross-sectional studies, as outlined in Section 2.1, and to an approach where we only adjusted for sickness status as a fixed effect.

For the aPCoA approach, we first stratified all data points by time. Within each stratum, we embedded the simulated microbial counts into an Aitchison distance, generated a kernel matrix, and obtained the kernel PCs. We then regressed each kernel PC on sickness status in a linear model, computed the residuals, and derived the PCs from the resulting residuals matrix. Finally, we plotted PC2 against PC1 for each time point.

For the fixed-effect-only approach, we embedded all simulated microbial counts Y into an Aitchison distance, generated a kernel matrix K, and obtained the kernel PCs. We then regressed each kernel PC on sickness status in a linear model, computed the residuals, and derived the PCs from the resulting residuals matrix. Finally, we plotted PC2 against PC1 for each time point.

For the proposed aPCoA approach for repeated measures, we embedded the simulated microbial counts Y into an Aitchison distance, which was used to generate a kernel matrix K. We then obtained the kernel PCs (Φ) from K and retained the top ℓ=62 kernel PCs, which explained approximately 90.0% of the variability in K. Each of the ℓ kernel PCs was regressed on sickness status as a fixed effect, and a random intercept for each subject, using a linear mixed model. The estimated standardized residuals were then computed, an adjusted kernel matrix was constructed, and the PCs of the adjusted kernel matrix were obtained. Finally, we plotted PC2 against PC1 for each time point.

We generated yi,1(k), i∈, k∈ the same way we generated yi,0(k) in Section 2.3.1. Next, we jointly sampled yi,2(k) and yi,3(k), i∈, k∈ from a multivariate normal distribution with mean yi,1(k)yi,1(k)′ and covariance 17103310. After generating these taxa counts, we introduced treatment effects by multiplying the counts of 20 randomly selected taxa by 8 for yi,2(k) and by multiplying the counts of 20 different randomly selected taxa by 32 for yi,3(k), i∈, k∈. Finally, we rounded all counts to the nearest whole number, truncating any negative values to 0.

We aimed to compare visualizations that either account for or ignore the confounding effect of cluster (familial) membership on the treatment effect. We applied the standard PCoA approach as in Section 2.1, making no adjustments. We compared this to the proposed aPCoA approach for repeated measures as in Section 2.2. Following the same procedure as before, we retained the top ℓ=29 kernel PCs, which explained 88.13% of the variability. Each kernel PC was then regressed on a random intercept for each family. We then computed standardized residuals, constructed the corresponding kernel matrices, and obtained the resulting PCs.