1 Introduction

Cancer is a heterogeneous disease characterized by diverse pathogenic mechanisms and clinical features (Wang et al., 2023). Research has shown that genomic alterations, such as copy number variations and somatic mutations, can lead to cancer development (Xu et al., 2023). Due to high heterogeneity, patients with similar phenotypes often exhibit different genomic changes, resulting in varied symptoms among cancer subtypes, which significantly impacts clinical diagnosis and prognosis (Jin et al., 2023). A major focus in current cancer research is predicting molecular subtypes using multi-omics data (Livesey et al., 2023; Chen et al., 2023). Classifying cancer subtypes can enhance our understanding of cancer pathogenesis and aid in personalized treatment approaches (Sosinsky et al., 2024).

Early research on cancer subtype discovery primarily concentrated on single omics data, such as gene expression data, using general clustering algorithms (Rappoport and Shamir, 2018). However, with the rapid accumulation of diverse omics data and the development of extensive cancer genome databases, the field has evolved significantly. One notable resource is The Cancer Genome Atlas (TCGA) (Akbani et al., 2014; Baird and Roychoudhuri, 2024), which has extensively studied multi-omics data from various cancer types across numerous patient samples. This wealth of sequencing data offers unprecedented opportunities to utilize multi-omics approaches for the discovery of cancer subtypes, paving the way for more precise and comprehensive cancer research and treatment strategies.

Researchers have proposed various methods for predicting cancer subtypes using multi-omics data. The simplest approach involves concatenating different biological data to form a single input matrix, followed by applying general clustering methods to identify cancer subtypes. For instance, Wu et al. (2015) introduced a comprehensive probability model called LRAcluster, based on low-rank approximation, to swiftly mine the shared main features across multiple omics data types. However, such methods often overlook differences in distribution and dimensionality among omics data, making it challenging to accurately characterize the input features. To address this, more sophisticated clustering strategies have been developed that consider the unique characteristics of each data source. The iCluster model (Shen et al., 2009) assumes that each omics dataset contains latent variables and employs a sparse method for gene selection and clustering. However, iCluster is limited to clustering continuous data types. Building on this, Mo et al. (2013) proposed iClusterPlus, an algorithm capable of jointly modeling multiple types of omics data, including continuous, count, and binary data. Additionally, Shi et al. designed the PFA algorithm (Shi et al., 2017), which maps each type of omics data to its corresponding low-dimensional space and performs automated information alignment and bias correction to achieve global pattern fusion in the feature space. These advancements offer more accurate and nuanced approaches to cancer subtype prediction, leveraging the full potential of multi-omics data.

The approaches mentioned primarily emphasize the representational characteristics of omics data while neglecting the structural insights that can illuminate similarities among patients, which are crucial for effective data learning. Spectral clustering (Luxburg, 2007) stands out as a method that captures such structural features by constructing graphs from data samples and leveraging graph-based clustering. Building on spectral clustering, various data integration algorithms have been developed. For instance, Wang et al. (2014) introduced the SNF method, which establishes similarity networks for diverse omics data types and integrates these networks using non-linear fusion techniques, thereby exploiting the complementary nature of the data. Expanding on these concepts, Ma and Zhang (2017) proposed the ANF method, which constructs K-nearest neighbor (KNN) networks for different omics datasets. These individual networks are then amalgamated into a unified fusion network using a random walk approach. To address the optimization challenges of spectral clustering, Yu et al. (2019) employed a linear search technique on the Stiefel manifold space, culminating in the MVCMO algorithm designed specifically for clustering multi-omics data. These advancements not only enhance our ability to extract meaningful insights from omics data but also underscore the importance of structural information for more robust data analysis and learning.

Deep learning has rapidly emerged as a research hotspot in the field of Artificial Intelligence (AI), especially in image data processing. Many deep learning-based methods for processing omics data have also been proposed to address the problem of cancer subtype discovery. Chen et al. (2020) proposed the DeepType algorithm for cancer classification, which combines supervised learning, unsupervised learning, and dimensionality reduction to learn data representations with clustering structures. Way and Greene (2018) utilized Variational Autoencoders (VAE) to compress gene expression features, thereby uncovering biologically relevant latent spaces. Xu et al. (2019) employed a Stacked Autoencoder (SAE) model to learn high-level representations of each omics data type, integrating these representations into an autoencoder layer to achieve a complex representation. They then used a Deep Flexible Neural Forest (DFNForest) model to classify the samples. These methods leverage deep learning to extract high-level feature representations from omics data and predict cancer subtypes based on these learned features. However, they often do not utilize the structural information inherent in omics data, which can be crucial for a more comprehensive understanding and prediction of cancer subtypes.

Graph Convolutional Networks (GCNs) (Thomas and Kipf, 2017) extend Convolutional Neural Networks (CNNs) to graph structures from the perspective of spectral theory (Bruna et al., 2013) (Defferrard et al., 2016). GCNs integrate the connectivity and characteristics of graph-structured data, and it has been demonstrated that GCNs and their variants (Hamilton et al., 2017; Veličković et al., 2017; Dai et al., 2018; Chen et al., 2017) significantly outperform Multi-Layer Perceptron (MLP) networks and traditional graph learning methods (Tang et al., 2015; Perozzi et al., 2014; Grover and Leskovec, 2016). To obtain high-level representations and fully utilize the spatial structure characteristics of omics data, we propose a new multi-omics deep clustering algorithm for discovering cancer subtypes, called Self-supervised Multi-fusion Strategy Network (SMMSN). SMMSN utilizes GCNs and SAEs to achieve the fusion of representation and structural information. It introduces various multi-omics data fusion strategies, ultimately achieving clustering through a self-supervised mechanism. This approach ensures efficient integration and utilization of information within and between omics data, leading to more accurate and insightful cancer subtype discovery.

The main contributions of our work are as follows.

(1) Integration of Structured and Representation Information. We introduce a novel method for integrating both structured and representation information within omics data. This approach aims to comprehensively harness and effectively learn the diverse and rich information inherent in multi-omics datasets.

(2) Multi-omics Data Fusion. We present two distinct methods for fusing multi-omics data: error reconstruction fusion and adaptive weighting network fusion. These methods are tailored to different aspects of data representation fusion, offering versatile strategies adapted to specific data characteristics.

(3) Dual Self-supervised Learning. We design a dual self-supervised learning module to perform unsupervised training on fused representations. By leveraging a self-supervised loss function, SMMSN enables the discovery of cancer subtypes from multi-omics fusion data without the need for real labels.

(4) Experimental Validation and Clinical Relevance. Experimental results compared with other algorithms and Kaplan-Meier survival curves demonstrated that SMMSN effectively distinguishes cancer subtypes with significant survival differences. In our analysis of Glioblastoma Multiforme (GBM) and Breast Invasive Carcinoma (BIC), the findings underscored SMMSN’s capability to discover clinically relevant cancer subtypes.

2 Materials and methods

The framework of our SMMSN for cancer subtype discovery based on multi-omics (Take DNA methylation data and mRNA expression data, for example,) is shown in Figure 1. SMMSN contains four main modules: A) Date Representation, B) Information Fusion Learning, C) Multi-omics Fusion, D) Dual Self-supervised Learning. The general clustering process of SMMSN is presented as follows.

① Date Representation Module. For the v-th omics data Xv, a KNN graph Av is constructed to obtain the structure information. At the same time, the feature representation is initialized and taken as input to the SAE network.

② Information Fusion Learning Module. Based on the KNN graph Av, a multi-layer GCN model is used to obtain the high-order structure representation Gvl−1, which is the output of the l−1 layer in the neural network. At the same time, SAE is used to learn the feature representation Zvl−1 of the omics data by using Xv. Then Gvl−1 and Zvl−1 are combined to obtain a joint representation Hvl−1 that contains both high-level structural information and feature information. The output of the SAE is Zvl, and the output of the GCN is Gvl which is obtained by Hvl−1. In this way, the structure information and feature information can be introduced into the deep clustering model through Gvl.

③ Multi-omics Fusion Module. According to the characteristics of different data representations, two data fusion methods are proposed to integrate the information of multiple omics data. For the GCN network output Gvl, an adaptive weighting network is designed to obtain GCN fusion representation Gfusion. For the SAE network output Zvl, an error reconstruction method is proposed to obtain SAE fusion representation Zfusion.

④ Dual Self-supervised Learning Module. A dual self-supervised module is used to jointly learn Gfusion and Zfusion to achieve end-to-end training of the entire model. Firstly, the probability distribution matrix Q containing the sample clustering information is calculated according to Zfusion. Through learning high-confidence distribution to make the data representation closer to the cluster center and the target probability distribution matrix P is obtained. We use the softmax function to perform multi-classification on Gfusion, and obtain the probability distribution matrix G. Finally, P is used to perform supervised training on the probability distribution matrices Q and G.

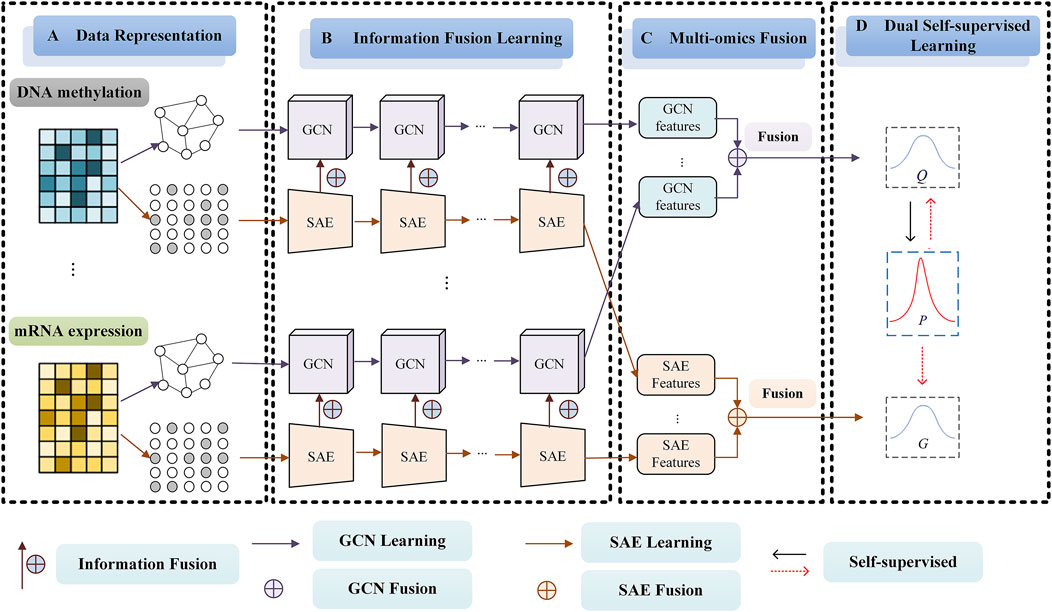
Figure 1. The framework of our proposed SMMSN model for cancer subtype discovery based on multi-omics (Take DNA methylation data and mRNA expression data, for example,). SMMSN contains four main modules: (A) Date Representation, (B) Representation Fusion Learning, (C) Multi-omics Fusion, (D) Dual Self-supervised Learning.

After the iteration is completed, the probability distribution matrix G contains both the feature representation information and structure information of the data. Therefore, the cluster label Y is calculated according to G.

2.1 Data representation module

Given multiple omics datasets X=X1,X2,⋯,Xv,⋯,XV, where V represents the number of datasets, Xv∈RN×mv is the v-th omics data in X, mv represents that the v-th omics data has m genes (features), and N represents the number of patients (samples). Prior to implementing our SMMSN model, we carried out several preprocessing steps to address outliers within the multi-omics data. First, any patient with more than 20% missing information in a particular data type was excluded from analysis. Similarly, biological features (such as mRNA expression) with over 20% missing values across all patients were also removed. Additionally, normalization was applied using the following formula:

In Equation 1 f is any biological feature, fn is the corresponding feature after normalization, Ef and Varf represent the mean and variance of f, respectively.

The aim of data representation module is to construct the input of GCNs and SAEs. For GCNs, we use the adjacency matrices constructed from the original data matrices of different omics as input. Since the adjacency matrix represents the relationship information between patient samples, and the number of patients is consistent across all omics data, the input matrix for each omics data in the GCN is of size N×N, where N is the number of patients. For SAEs, the input feature dimensions of different omics data can vary, but after being compressed by the encoder, the encoded representations of each type of omics data can be mapped to the same latent space dimension. This means that although the input features of the omics data differ, their output feature dimensions can be aligned through the encoder. In this way, even if the original feature dimensions of different omics data are inconsistent, the autoencoder can compress them into feature representations of the same dimension, allowing these features to be processed consistently in subsequent fusion operations.

Therefore, we take the matrix after the initialization of the omics data as the SAE input, and the vth omics data is still represented by Xv. A KNN graph is constructed as the input of GCN based on each omics data. For each sample of each omics data, we select its top-K similar samples as neighbors to calculate the similarity between it and each neighbor, and then construct the similarity matrix Sv∈RN×N. We use the heat kernel method to construct the KNN graph, and the similarity between the two samples i and j can be written as

In Equation 2 σ represents heat kernel parameter. Then the top-K similar samples of each omics data are defined as neighbors to form the adjacency matrix Av∈RN×N.

2.2 Information fusion learning module

This subsection contains three processes: GCN learning, SAE learning and information fusion learning. The whole information fusion learning process of single omics data can be found in Figure 2 (Take DNA Methylation data for example).

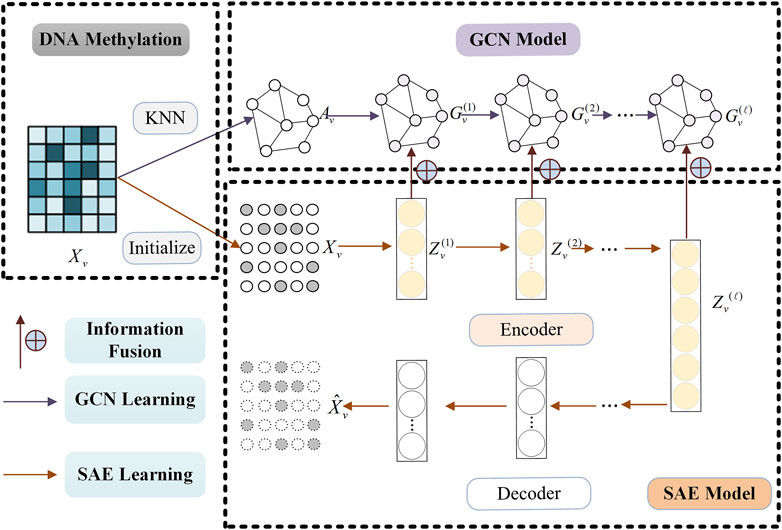
Figure 2. Information fusion learning process of single omics data (Take DNA Methylation data, for example,) by combining SAE and GCN model.

2.2.1 Stacked autoencoder learning

It is critical to learn effective feature representation in clustering tasks. Compared with traditional methods, deep learning methods can extract more advanced data feature representations and are widely used in various fields. In order to extract the high-level feature representation of omics data, we use the Stacked Autoencoder (SAE) model with the strongest generalization performance to learn the original omics data. The training process of SAE model can be found in Figure 2 (See SAE Model).

Suppose there are l layers in the SAE. In the encoder stage, when SAE is used to learn omics data Xv, the learning of the l-th layer is written as Zvl

Zvl=ϕWevlZvl−1+bvle(3)

In Equation 3 ϕ is the activation function of the full connection layer. Here we use the LeakyRELU activation function. Wvle and bvle are the weight matrix and bias of the l-th layer in the encoder, respectively. When the encoder starts learning, the feature representation is initialized as: Zv0=Xv.

In the decoder stage, the input data is reconstructed through multiple fully connected layers, which can be written as

Zvl=ϕWvldZvl−1+bvld(4)

In Equation 4 Wvld and bvld are the parameters of l-th layer in the decoder.

The final output Zvl is the output X^v of SAE: X^v=Zvl. We hope that X^v can reconstruct the original omics data Xv as much as possible, and then use the following loss function in Equation 5 for SAE model training

Lres=12N∑vVX^v−XvF2(5)2.2.2 Graph convolutional network learning

SAE can learn the advanced feature representation of omics data, but it does not consider the structural information among omics data samples. We introduce Graph Convolutional Network (GCN) to learn the structural representation of each omics data. The training process of GCN model can be found in Figure 2 (See GCN Model).

For omics data Xv, GCN learns the structural representation Gvl of the l-th layer through the following convolution operations

Gvl=CA^vGvl−1Wvl−1(6)

where Wvl−1 is the weight matrix of l−1-th layer. A^v=Av+I, where I is an identity matrix. According to Equation 6, GCN can learn the representation Gvl of the next layer through Gvl−1, Wvl−1 and the adjacency matrix A^v.

2.2.3 Information fusion learning

The information fusion learning process of single omics data by combining SAE and GCN model can be found in Figure 2. Considering both Zvl−1 and Gvl−1, we can obtain a joint representation Hvl−1 with more effective information through the following formula

Hvl−1=1−εGvl−1+εZvl−1(7)

where ε is the balance parameter used to balance the relationship between the two representations Zvl−1 and Gvl−1. For simplicity, we set it to 0.5. Through Equation 7, we have realized the connection between SAE and GCN network. And Hvl−1 contains both feature representation information and structure representation information.

Next, we need to learn the l-th layer representation Gvl of GCN. At this time, Hvl−1 is taken as the input of GCN. Then we have

Gvl=CA^vHvl−1Wvl−1(8)

In the traditional GCN model, after the multi-layer graph convolution operation is adopted, the characteristics of different nodes tend to be homogenized, that is, the characteristics of all nodes within the same connected component are almost the same. This is the so-called over-smoothing phenomenon. The representation information learned by the SAE in each layer is very different, and in Equation 8, the joint representation Hvl−1 contains both the feature information learned and the structured information learned. Therefore, the existence of Equation 7 can alleviate the over-smoothing problem of GCN.

It is worth noting that the input data matrix Gv1 of the first layer can be calculated by using omics data Xv. Gv1 can be defined by Equation 9

The final output of GCN is determined according to Equation 10

Gvl=CA^vHvl−1Wvl−1(10)2.3 Multi-omics fusion module

After learning the feature representation and structural representation of any kind of omics data, in order to realize the further clustering task, it is necessary to fuse multi-omics data representations. Based on the different characteristics of omics data representations, we propose two multi-omics data fusion ideas: adaptive weighting network fusion and error reconstruction fusion, to implement Feature Representation Fusion (FRF) and Structural Information Fusion (SIF), respectively. The detailed fusion process can be found in Figure 3.

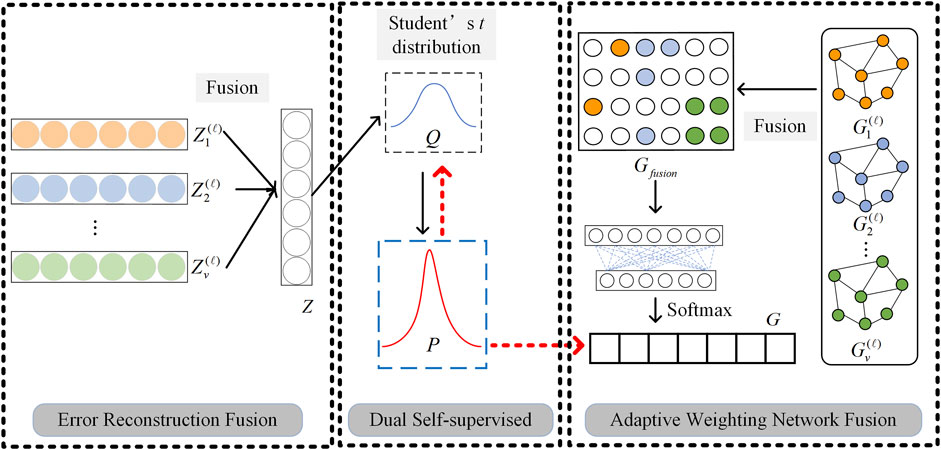
Figure 3. Graphical illustration of two multi-omics data fusion strategies and dual self-supervised learning.

For the GCN output Gvl of each omics data, we connect them in series and propose an adaptive weighting network for fusion to obtain a fusion representation Gfusion∈RN×N

Gfusion=G1l∥G2l∥⋯∥GVlWfusion(11)

where Wfusion∈RVN×N is a weight matrix that needs to be learned in the fusion process. Since Gvl contains the structural information of the omics data, it is necessary to consider the correlation between the samples in the fusion process. Therefore, in Equation 11, we first connect Gvl of each omics data to form an overall joint matrix, and then use Wfusion to perform weighted learning, so that the adaptive weighting of all samples of all omics data is realized. After obtaining Gfusion, we use the softmax function to perform multiple classifications to obtain a probability distribution matrix G, where gij∈G denotes the probability that the sample i belongs to category j.

For the SAE output Zvl of each omics data, we propose an error reconstruction fusion method to obtain a fusion representation Z∈RN×N. First, Zvl is initialized, and then it is learned according to the following loss function

Lfus=∑v=1VZ−ZvlF2(12)

Following Equation 12, our method can learn the fusion representation with the smallest error of all omics data feature representation through this data reconstruction idea.

2.4 Dual self-supervised learning module

Traditional SAE and GCN are unsupervised learning and semi-supervised learning algorithms respectively, which cannot be directly applied to clustering problems. In this paper, the dual self-supervised method is used to uniformly train the multi-omics data fusion representation learned by SAE and GCN to realize the clustering task. Graphical illustration of dual self-supervised learning is given in Figure 3.

Firstly, K-means algorithm is adopted to cluster the fusion representation Z of SAE, and get c initial cluster centers, where c is the number of clusters. For the i-th sample Zi (the i-th row of Z) and the j-th cluster center μj of Z, we use the student’s t distribution in Equation 13 (Dunnett and Sobel, 1954) to measure the similarity between them (Tao et al., 2019; Wang et al., 2018)

qij=1+Zi−μj2/δ−δ+12∑j′1+Zi−μj′2/δ−δ+12(13)

where δ is the degree of freedom of student’s t distribution, qij is the probability that the i-th sample is allocated to the j-th cluster center. The probability distribution matrix of all sample assignments can be denoted as Q, and qij∈Q.

Then we optimize Z by learning high-confidence assignments to make the data representation closer to the cluster center. In Equation 14, the target distribution matrix pij∈P can be obtained according to Q

pij=qij2/fj∑j′qij2/fj′(14)

where fj=∑iqij. In P, all assignments have higher confidence.

In order to minimize the loss between Q and P, KL divergence is used as the loss function

Lclu=KLP∥Q=∑i∑jpij⁡logpijqij(15)

Equation 15 can make the data representation closer to the cluster center, which is conducive to data clustering. P is calculated by Q, and the update of Q needs to rely on P. Therefore, this is a self-supervised learning mechanism.

We also perform self-supervised learning on the fusion representation of GCN. Since we have obtained the probability distribution matrix G of GCN output, we can directly use P and G to perform supervised learning. That is

Lgcn=KLP∥G=∑i∑jpij⁡logpijgij(16)

Through the above-mentioned dual self-supervised learning mechanism, the target distribution P conducts supervised learning on Q and G respectively in Equations 15, 16, so that the fusion output representations of GCN and SAE are unified under the same optimization framework. After iteration and update, the final training results tend to be consistent.

In conclusion, the overall loss function of the proposed SMMSN framework is defined as Equation 17

L=Lres+λ1Lfus+λ2Lclu+λ3Lgcn(17)

where λ1, λ2 and λ3 are hyperparameters used to balance different loss functions.

Since the final output G of SMMSN model contains both the representation information and structure information of the data, in Equation 18, we use