1 Introduction

Monitoring mental health through electroencephalography (EEG) has become an increasingly important area of research due to the growing recognition of mental health issues and the need for non-invasive, objective, and continuous monitoring methods. EEG, with its ability to capture the brain's electrical activity in real-time, offers unique insights into the neural processes underlying various mental health conditions (Michelmann et al., 2020). Not only can EEG provide a window into the brain's functioning, but it can also help in the early detection and management of mental disorders (Gao et al., 2021). Furthermore, EEG-based monitoring is crucial for developing personalized treatment plans and improving patient outcomes, making it a vital tool in both clinical and research settings (Cassani et al., 2018). The significance of EEG in mental health monitoring lies not only in its diagnostic potential but also in its ability to track changes over time, offering a dynamic view of the brain's response to treatment and environmental factors (Krigolson et al., 2017). As mental health issues continue to rise globally, the need for effective monitoring tools like EEG has never been more critical (Goswami et al., 2022).

Traditional machine learning methods in EEG analysis, while foundational, exhibit several critical limitations that hinder their effectiveness in mental health monitoring applications. Early methods predominantly relied on handcrafted features extracted from EEG signals, such as power spectral density and coherence (Kumar and Mittal, 2018). These features, although useful, capture only a limited view of the rich information contained within EEG signals. Specifically, handcrafted features often focus on static, time-averaged characteristics, neglecting the complex and dynamic temporal dependencies present in EEG data. Such simplifications are inadequate for understanding the rapidly fluctuating brain activities that are essential for accurate mental health monitoring. Moreover, conventional classifiers like support vector machines (SVMs) and k-nearest neighbors (k-NN) often struggle to model the intricate spatial relationships across multiple EEG channels, which are crucial for detecting patterns associated with mental health conditions (Delorme and Makeig, 2004). These algorithms treat the signals from each electrode independently or rely on shallow features that fail to account for inter-channel dependencies. As a result, they lack the capacity to capture the synchronized activity patterns across brain regions, which are vital for identifying neural biomarkers related to mood, anxiety, or cognitive states. Another significant limitation is the inability of traditional machine learning models to effectively handle the high-dimensional and non-linear nature of EEG data. Methods like SVMs and k-NN typically perform well only in controlled, small-scale settings where data variability is minimized. When applied to larger, real-world EEG datasets, these models tend to exhibit poor generalizability due to their limited capacity to handle the variability and noise inherent in complex EEG signals (Lotte et al., 2018; Craig and Tran, 2020; Alhussein et al., 2019). This restricts their application to controlled laboratory environments, rendering them less useful for real-time, in-the-wild mental health monitoring, where factors such as individual differences, movement artifacts, and environmental noise are present. Traditional machine learning approaches in EEG analysis are constrained by their reliance on handcrafted features, their inability to capture both spatial and temporal complexities, and their limited adaptability to high-dimensional, noisy datasets. These limitations underscore the need for more advanced methods capable of leveraging the full spatio-temporal dynamics of EEG signals to enhance the accuracy and robustness of mental health monitoring in diverse real-world contexts.

Recent innovations have turned to graph-based deep learning methods, particularly Graph Convolutional Networks (GCNs) (Roy et al., 2019) and Graph Attention Networks (GANs) (Kwon et al., 2019), to address the unique structural properties of EEG data. GCNs are highly effective in representing the brain as a graph of interconnected regions, allowing models to capture both localized and global patterns of neural activity (Zhao et al., 2019). For instance, Craik et al. (2019) demonstrated the utility of GCNs in brain network analysis, highlighting their capability to model hierarchical dependencies. However, these methods often struggle to integrate temporal dynamics effectively. Attention mechanisms, particularly spatiotemporal attention models, have further refined the ability to extract critical features from EEG data. These methods dynamically assign weights to relevant time points and spatial regions, enhancing interpretability and robustness. When combined with GCNs, attention mechanisms provide a powerful framework for modeling the brain's complex and dynamic activity (Tsiouris et al., 2018). Multimodal approaches incorporating EEG with other physiological signals, such as electromyography (EMG) and electrocardiography (ECG), have also shown promise. These methods offer a holistic view of mental states, combining complementary data to improve classification accuracy and resilience against noise. Studies have demonstrated their potential in contexts like stress detection and cognitive load estimation, where single-modality approaches may falter (Sturm et al., 2021).

The field has recently advanced toward more sophisticated models that integrate machine learning techniques with personalized and remote health monitoring. This latest phase has witnessed the adoption of graph-based models, such as Graph Convolutional Networks (GCNs) and Graph Attention Networks (GANs), which are particularly suited for EEG data due to their ability to model the brain's complex network structure (Parisot et al., 2018). These models capture both localized and global patterns of connectivity across brain regions, creating a nuanced understanding of spatial interactions (Song et al., 2021). By incorporating temporal dynamics into these graphs, researchers have developed interpretable, multi-scale models that better support personalized mental health monitoring (Sihag et al., 2022). This phase also emphasizes scalability, allowing EEG-based models to be deployed in practical settings. However, issues such as data privacy, ethical considerations, and continuous improvements in accessibility remain important challenges (Plis et al., 2018; Varatharajan et al., 2022; Stahl et al., 2019).

While traditional machine learning methods and early deep learning models struggle to capture the dynamic, multi-scale dependencies in EEG data, recent graph-based and attention-driven approaches have only partially bridged this gap by focusing on either spatial or temporal aspects independently. Additionally, these methods often lack scalability and adaptability to personalized, real-world applications, especially in resource-limited settings where data privacy and interpretability are paramount concerns. Our EEGMind-Transformer model addresses these limitations by integrating advanced graph-based neural networks with temporal attention mechanisms, allowing the model to simultaneously capture intricate spatiotemporal patterns within EEG data. This comprehensive approach not only enhances interpretability by offering insight into specific brain region interactions relevant to mental health but also improves scalability for remote and clinical applications through a structure that is adaptable across different datasets and user scenarios. By effectively bridging the gaps in current methods, the EEGMind-Transformer provides a robust, scalable, and interpretable solution tailored for personalized and continuous mental health monitoring.

• The EEGMind-Transformer introduces Dynamic Temporal Graph Attention Mechanism (DT-GAM), Hierarchical Graph Representation and Analysis (HGRA), and Spatial-Temporal Fusion Module (STFM) to effectively capture complex spatiotemporal dependencies in EEG data.

• This method is highly versatile and efficient, suitable for various scenarios, consistently delivering excellent performance across different mental health monitoring applications while offering model interpretability and scalability.

• Experimental results demonstrate that EEGMind-Transformer significantly outperforms existing state-of-the-art methods across multiple datasets, achieving superior performance.

2 Related work 2.1 Machine learning in EEG analysis

Traditional machine learning techniques have been extensively used in EEG analysis for mental health monitoring. These methods typically involve feature extraction followed by classification using algorithms such as Support Vector Machines (SVM), k-Nearest Neighbors (k-NN), Random Forests, and shallow neural networks (Lakshminarayanan et al., 2023). Feature extraction often relies on domain expertise to identify relevant features from the EEG signals, such as power spectral density, coherence, and wavelet coefficients, which are then fed into classifiers to distinguish between different mental states. While these approaches have shown some success, they are limited by their reliance on handcrafted features, which may not capture the full complexity of the EEG data (Hong et al., 2024). Moreover, traditional classifiers often struggle with the high dimensionality and variability of EEG signals, leading to issues with overfitting and poor generalization across different populations and recording conditions (Wan et al., 2023). Furthermore, these methods are typically static and cannot adequately model the temporal dynamics inherent in EEG signals, which are crucial for understanding cognitive and emotional processes. As a result, while traditional machine learning approaches have laid the groundwork for EEG analysis, they are often insufficient for capturing the complex, non-linear patterns in the data that are essential for accurate mental health monitoring (LaRocco et al., 2023).

2.2 Deep learning in EEG analysis

Deep learning has emerged as a powerful alternative to traditional machine learning methods in EEG analysis, offering the ability to automatically learn features directly from the data. Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNNs), including Long Short-Term Memory (LSTM) networks, have been particularly popular (Simar et al., 2024). CNNs are well-suited for capturing spatial patterns in EEG data by treating the multichannel signals as images or matrices, while RNNs and LSTMs excel at modeling temporal dependencies by processing EEG signals as sequences (Akter et al., 2024). More recent work has explored the use of hybrid models, such as CNN-LSTM architectures, which combine the strengths of both approaches to capture both spatial and temporal features simultaneously (Lakshminarayanan et al., 2023). While these methods have improved performance over traditional machine learning techniques, they still face challenges. One significant limitation is their inability to fully capture the complex spatiotemporal dependencies present in EEG data. Additionally, these models often require large amounts of labeled data for training, which can be difficult to obtain in clinical settings. Furthermore, despite their complexity, deep learning models can sometimes act as “black boxes,” offering little interpretability of how decisions are made, which is a critical requirement in medical applications (Ai et al., 2023).

2.3 Graph-based approaches in EEG analysis

Graph-based approaches have gained traction in EEG analysis due to their ability to model the brain's complex network structure. Graph-based methods are particularly effective in capturing the spatial dependencies and interactions within the brain, which are often overlooked by traditional machine learning and even some deep learning methods. Techniques such as Graph Convolutional Networks (GCNs) (Wu et al., 2019) and Graph Attention Networks (GANs) have been applied to EEG data, enabling the capture of both local and global patterns of brain connectivity. These methods can dynamically model how different brain regions interact over time, providing a more nuanced understanding of the underlying neural mechanisms associated with mental health conditions (Kosaraju et al., 2019). One of the significant advantages of graph-based methods is their interpretability, as they can highlight specific brain regions or connections that are most relevant to the task at hand. However, challenges remain, particularly in integrating temporal information with the spatial graph structures, as traditional graph-based methods primarily focus on static representations (Wu et al., 2022). Recent advances have started to address this by incorporating temporal dynamics into graph models, but there is still much work to be done to fully realize the potential of graph-based approaches in EEG analysis (He et al., 2023). These methods represent a promising direction for future research, particularly in their ability to provide both high accuracy and interpretability in mental health monitoring applications.

3 Preliminaries

To effectively model and monitor mental health conditions using EEG signals, it is essential to formalize the problem in a manner that aligns with the capabilities of the EEGMind-Transformer architecture. The goal is to detect and monitor various mental health conditions by analyzing the patterns and abnormalities present in EEG data. This can be framed as a classification problem where the model is trained to distinguish between different mental states based on the input EEG signals.

Let D=i=1N represent a dataset of EEG recordings, where Xi∈ℝC×T denotes the EEG data for the i-th sample, C is the number of EEG channels, T is the number of time steps, and yi ∈ is the corresponding mental health condition label, with K being the total number of classes. The goal is to learn a function that maps EEG data to the correct mental health condition.

To facilitate the learning process, the EEG data Xi is first preprocessed to remove noise and artifacts, resulting in a clean signal X~i. This preprocessing step includes operations such as band-pass filtering, Independent Component Analysis (ICA) for artifact removal, and normalization. The preprocessed signal X~i is then segmented into overlapping windows of fixed size, each corresponding to a smaller time frame of the EEG recording.

X~ij∈ℝC×W    (2)

denote the j-th window of the i-th EEG recording, where W is the window size.

The EEGMind-Transformer processes each window X~ij independently through a series of transformations designed to capture the spatial and temporal dependencies within the EEG data. The model leverages a spatio-temporal attention mechanism, which can be mathematically represented as:

Aij=softmax ((Qij)(Kij)⊤dk)Vij    (3)

Here, Qij,Kij,Vij are the query, key, and value matrices obtained from the linear transformation of the input window X~ij, and dk is the dimensionality of the keys. The attention mechanism computes the weighted sum of the values Vij, where the weights are determined by the similarity between the queries and keys.

Subsequently, the outputs of the attention mechanism for all windows of the EEG recording are aggregated to form a comprehensive representation of the entire EEG signal. This representation is then passed through a graph neural network (GNN) that models the relationships between different brain regions. The GNN is defined on a graph G = (V, E), where V represents the set of brain regions (nodes), and E represents the connections (edges) between these regions. The graph convolution operation at each layer of the GNN can be expressed as:

H(l+1)=σ(D-12AD-12H(l)W(l))    (4)

where H(l) denotes the node features at the l-th layer, A is the adjacency matrix of the graph, D is the degree matrix, W(l) is the trainable weight matrix, and σ is a non-linear activation function. The final output of the GNN represents the spatial dependencies between different brain regions and is concatenated with the temporal features extracted by the Transformer.

Finally, the concatenated features are fed into a fully connected layer followed by a softmax function to produce the probability distribution over the mental health condition classes:

y^i=softmax (Wfhi+bf)    (5)

where Wf and bf are the weights and biases of the fully connected layer, and hi is the concatenated feature vector.

The training objective is to minimize the cross-entropy loss between the predicted labels ŷi and the true labels yi:

L(θ)=-1N∑i=1N∑k=1Kyi,klog(y^i,k)    (6)

where θ represents all the trainable parameters in the model, and yi, k is a binary indicator (0 or 1) that indicates whether the class label k is the correct classification for sample i. This formalization sets the stage for the detailed exploration of the EEGMind-Transformer architecture and its components in the following sections.

4 Methodology 4.1 Overview

The EEGMind-Transformer introduces a breakthrough in mental health monitoring by integrating EEG signals with a Transformer-based framework. This model is engineered to exploit both temporal and spatial characteristics of the data, which are closely linked to mental health issues like depression and anxiety. Building on the latest progress in multimodal spatio-temporal attention mechanisms and the evolution of graph-based deep learning models for mental health assessment, the EEGMind-Transformer seeks to overcome the constraints of traditional approaches. It offers a more adaptable, interpretable, and scalable solution that works efficiently in real-time settings, thus making it suitable for both clinical and practical use cases. Designed to tackle the inherent challenges posed by EEG signal variability and the growing need for individualized models, this Transformer-based approach excels in capturing intricate patterns and long-range dependencies in data. Through the use of spatio-temporal attention, the model prioritizes the most critical features during training. The integration of graph neural networks allows for deeper insights into inter-regional brain activity, contributing to enhanced inference precision. This innovation is poised to significantly impact the future of mental health monitoring by offering a non-invasive, reliable, and versatile method for early detection and continuous mental health evaluation.

Dynamic Temporal Graph Attention Mechanism (DT-GAM): We designed the DT-GAM module to capture dynamic temporal dependencies in EEG data. Unlike traditional temporal modeling methods, DT-GAM uses a graph attention mechanism to adaptively adjust relationships between temporal nodes, ensuring that key features within specific time intervals receive prioritized attention. This design enhances the model's ability to capture temporal information, improving accuracy in predicting different mental health states. Hierarchical Graph Representation and Analysis Module (HGRA): The proposed HGRA module constructs a multi-level graph structure to better simulate the complex interactions between different brain regions. By aggregating information across different hierarchical levels, HGRA captures both local and global spatial dependencies. This innovation not only enhances the model's capacity to interpret brain structures but also provides greater interpretability, making it easier to visualize the significance of different brain regions in mental health monitoring. Spatial-Temporal Fusion Module (STFM): To seamlessly combine temporal and spatial information, EEGMind-Transformer introduces the STFM module. This module deeply integrates temporal and spatial features to create a comprehensive EEG signal representation. Compared to traditional methods that rely solely on spatial or temporal features, the addition of STFM significantly improves the model's depth of interpretation, allowing EEGMind-Transformer to gain a more holistic understanding of the complex changes associated with mental health states. Integrated Interpretability and Adaptability Design: EEGMind-Transformer not only achieves significant improvements in classification performance but also provides enhanced interpretability and extensibility through its modular design. Our approach can adapt to different datasets and scenarios while offering visual explanations for each module, making the model suitable for clinical diagnostics and personalized remote monitoring (Figure 1).

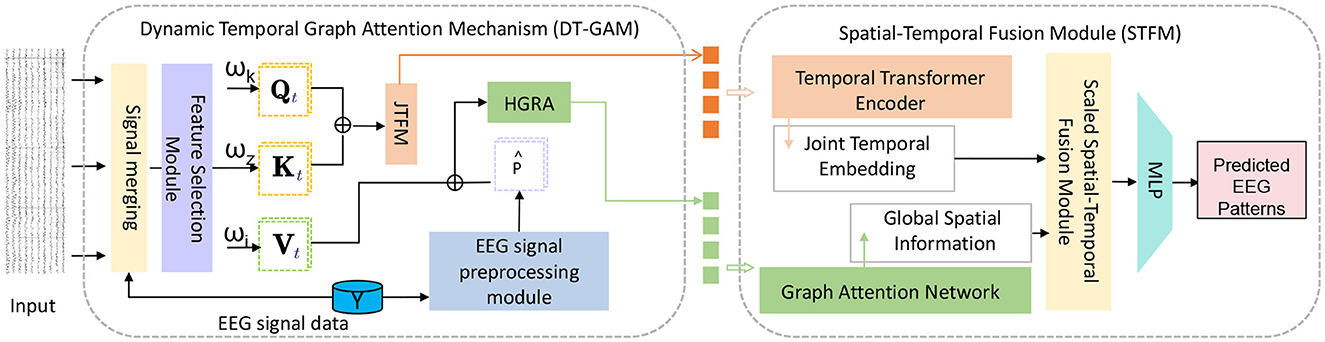
Figure 1. This figure illustrates the architecture of the EEGMind-Transformer model. It includes three core modules: Dynamic Temporal Graph Attention Mechanism (DT-GAM), Hierarchical Graph Representation and Analysis (HGRA), and Spatiotemporal Fusion Module (STFM). The DT-GAM module utilizes a graph-based attention mechanism to capture the underlying temporal dependencies in the EEG signals, emphasizing important temporal features. The Joint Temporal Feature Module (JTFM) further processes this temporal information to enhance the integration of joint temporal features, which are then passed to subsequent modules. The HGRA module builds a multi-level graph structure to capture local and global spatial dependencies, providing insights into complex cross-regional brain activities. Finally, the STFM combines the processed temporal and spatial features from DT-GAM, JTFM, and HGRA to obtain a comprehensive EEG signal representation.

4.2 Dynamic temporal graph attention mechanism (DT-GAM)

The Dynamic Temporal Graph Attention Mechanism (DT-GAM) lies at the heart of the EEGMind-Transformer, enabling the model to effectively capture complex temporal dependencies within EEG data. This mechanism is crucial for enhancing the model's ability to focus on the most relevant temporal features, which are vital for accurate mental health monitoring. DT-GAM leverages a graph-based representation of EEG data over time, where each node in the graph represents an EEG channel, and edges capture the temporal relationships between these channels across different time steps. The dynamic nature of this mechanism allows the graph to adapt its structure based on the evolving temporal patterns, ensuring that the most critical time points are given priority. The temporal attention mechanism can be mathematically formulated as:

Temporal-Attention (Qt,Kt,Vt)=softmax (QtKt⊤dt)Vt    (7)

where Qt, Kt, Vt are the query, key, and value matrices derived from the temporal features of the EEG data. The dimension dt serves as a scaling factor, which stabilizes the gradients during training. This attention mechanism allows the model to dynamically weigh the importance of different time steps, learning to focus on the temporal patterns that are most indicative of specific mental health conditions.

In DT-GAM, the temporal dependencies are modeled as a time-evolving graph Gt = (Vt, Et), where each node v ∈ Vt represents a time step, and each edge e ∈ Et represents the temporal connection between EEG readings at different times. The graph attention mechanism updates the importance of these connections through:

At=softmax (QtKt⊤dt)    (8)

where At represents the temporal attention scores that adjust the influence of each time step based on its relevance to the task. These scores modulate the interaction between nodes (time steps), allowing the model to adaptively focus on the most informative segments of the EEG data.

The output from the temporal attention mechanism is then processed through a temporal graph convolutional layer, which refines the temporal node embeddings by aggregating information from the relevant time steps:

Ht(l+1)=σ(AtHt(l)Wt(l))    (9)

Here, Ht(l) denotes the node embeddings at layer l, and Wt(l) are the learnable weights of the temporal graph convolution layer. This operation is iterated across multiple layers, enabling the model to capture higher-order temporal interactions in the EEG data.

The refined temporal features from DT-GAM are then integrated with spatial features using a fusion strategy that concatenates the temporal and spatial outputs, which are then processed through a fully connected layer:

hf=ReLU (Wf[ht;hs]+bf)    (10)

where ht and hs are the temporal and spatial feature vectors, respectively, and [·;·] represents concatenation. The fusion layer combines the temporal dynamics captured by DT-GAM with the spatial structure, producing a comprehensive representation of the EEG data.

Finally, the fused representation is passed through a softmax layer to generate the probability distribution over the mental health condition classes:

y^i=softmax (Wohf+bo)    (11)

where Wo and bo are the weights and biases of the output layer.

The DT-GAM thus enables the EEGMind-Transformer to dynamically adapt its focus on the most relevant temporal features, leading to more accurate predictions and providing deeper insights into the temporal dynamics of mental health conditions.

4.3 Hierarchical Graph Representation and Analysis

The EEGMind-Transformer model incorporates a Hierarchical Graph Representation and Analysis (HGRA) module to effectively capture the multi-scale dependencies inherent in EEG data. This module is designed to leverage the hierarchical structure of brain regions and their interactions, enabling the model to learn both local and global patterns associated with mental health conditions.

At the core of the HGRA module is the construction of a multi-level graph G = , where each graph Gl = (Vl, El) corresponds to a different level of granularity in the brain's functional architecture. The lowest level graph G1 represents individual EEG channels as nodes, with edges representing direct functional connections between these channels. Higher levels G2, …, GL aggregate these channels into larger regions or networks, capturing more abstract relationships between brain areas (Figure 2).

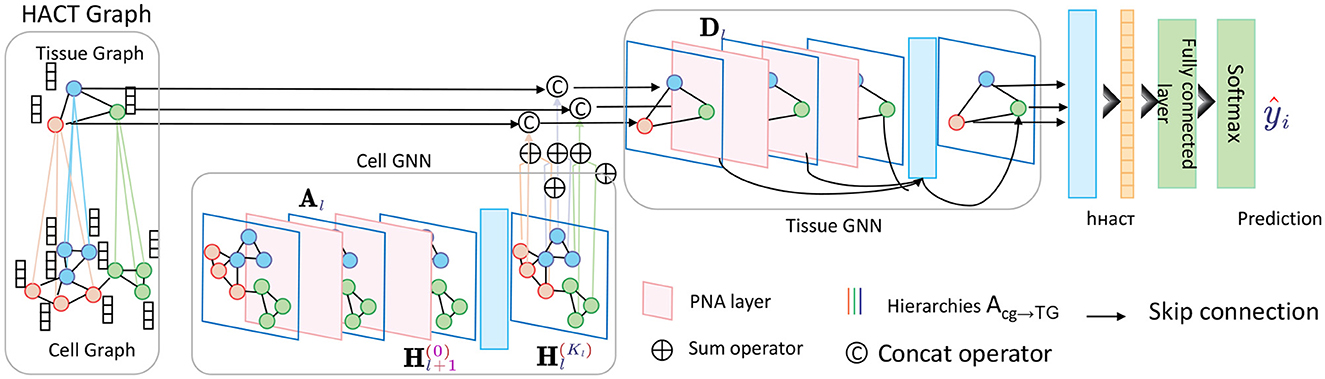
Figure 2. Schematic diagram of the Hierarchical Graph Representation and Analysis (HGRA) module. This module is used to capture multi-scale information in a hierarchical graph structure. The module contains Cell GNN (Cell Graph Neural Network) and Tissue GNN (Tissue Graph Neural Network), which apply PNA layer (Principal Neighborhood Aggregation) to aggregate node information at the cell and tissue levels, respectively. Through inter-layer aggregation (Acg→TG), the information in the cell graph is transferred to the tissue graph, realizing multi-level dependencies from local to global.

The node embeddings Hl(0) at each level l are initialized based on the features extracted from the EEG data, with lower levels receiving finer-grained features and higher levels receiving more abstract representations. The graph convolutional operations at each level can be described as:

Hl(k+1)=σ(Dl-12AlDl-12Hl(k)Wl(k))    (12)

where Al is the adjacency matrix of graph Gl, Dl is the degree matrix, Wl(k) is the weight matrix for the k-th layer at level l, and σ is a non-linear activation function. This operation iteratively refines the node embeddings by aggregating information from neighboring nodes, allowing the model to capture the hierarchical dependencies within the EEG data.

To integrate information across different levels of the hierarchy, the HGRA module employs a pooling mechanism that consolidates the node embeddings from lower levels and passes them to higher levels. This pooling operation can be formalized as:

Hl+1(0)=Pool (Hl(Kl))    (13)

where Hl+1(0) represents the initial embeddings for the next level, Hl(Kl) are the final embeddings at level l, and Pool(·) is a pooling function that aggregates information from lower-level nodes. Common pooling strategies include max pooling, average pooling, or more sophisticated attention-based pooling methods that weigh the importance of each node's contribution.

Principal Aggregation and Distribution (PAD) Layer: The HGRA module also incorporates a PAD layer (Principal Aggregation and Distribution layer) to further enhance the hierarchical graph structure. The PAD layer performs an aggregation operation across all levels, enabling a global representation by combining information from various scales. This aggregated representation is then distributed back to each level to reinforce local representations with global context, improving the model's ability to capture both global and local dependencies in EEG data.

The aggregation operation in the PAD layer can be expressed as:

Hglobal=Aggregate (⋃l=1LHl(Kl))    (14)

where Hglobal represents the global embedding aggregated across all levels l = 1, …, L, and Hl(Kl) is the final node embedding at level l. The Aggregate(·) function can be implemented as a sum, mean, or attention-based aggregation over all hierarchical levels.

The global representation Hglobal is then distributed back to each level to enrich the local embeddings with global context, which can be described as:

Hlenhanced=Hl