The neuronal network of the brain is a dynamic structure, constantly adapting to internal and external stimuli. Within the white matter, the local environment of neurons is found to modulate their axon morphology (Andersson et al., 2020). Especially glial cells play a significant role in this modulation. While the glial cells do not directly participate in neuronal signaling, they carry out crucial supporting tasks: myelination (oligodendrocytes), maintaining an appropriate chemical environment for neuronal signaling (astrocytes), and removing cellular debris from sites of injury or normal cell turnover (microglial) (Purves et al., 2001). To carry out these tasks, the glial cells move through the tissue. Such dynamic behavior has been observed with microscopy (Davalos et al., 2005; Nimmerjahn et al., 2005; Tønnesen et al., 2018). Furthermore, it has been found that the morphology of axons adapts in response to these environmental changes (Andersson et al., 2020). Moreover, there is a relation between the morphology and function of the individual neurons. Morphological factors that affect the axonal conduction velocity include the axon diameter (Hursh, 1939; Skoven et al., 2023), the myelin sheath thickness (Sanders and Whitteridge, 1946), and the length and spacing of nodes of Ranvier (Arancibia-Cárcamo et al., 2017). Quantifying the morphology of axons and brain white matter in general is thus of great interest for enhancing our understanding of various brain processes, and can provide a potential biomarker of disease.
The most promising method for assessing axon morphology non-invasively, is diffusion-weighted MRI (dMRI). dMRI reflects the morphological properties of the underlying tissue by measuring diffusion properties of water molecules within the tissue (Basser et al., 1994; Beaulieu, 2002; Alexander et al., 2019; Novikov et al., 2019). To advance the method even further, we need access to extensive experimentation for scan sequence optimization and biophysical model validation informed by known ground truths. This is unfeasible to obtain with either preclinical or clinical MRI due to the limited spatial resolution.
It is therefore of great interest to supplement dMRI research with numerical simulations, because these come with a ground truth. dMRI can with advantage be simulated based on Monte Carlo (MC) diffusion simulations (Hall and Alexander, 2009; Rafael-Patino et al., 2020). The level of realism in simulations is crucial for the specificity and applicability obtainable by the models developed based on them (Nilsson et al., 2012; Andersson et al., 2020; Brabec et al., 2020; Lee et al., 2020).
Mimicking the highly complex tissue of white matter is a great challenge. White matter has commonly been represented as idealized straight, coaxial, infinitely long, and non-touching cylinders (Novikov et al., 2019). However, from recent advances in 3D histology, it has been validated that the white matter has a much more complex configuration (Tønnesen et al., 2018; Abdollahzadeh et al., 2019; Lee et al., 2019; Andersson et al., 2020)(Abdollahzadeh et al., 2021). While individual axons are found to express non-circular cross-sections, longitudinal diameter variations, and tortuosity, axons on the ensemble scale are found to express orientation dispersion and crossing fibers. Furthermore, recent studies show that such characteristics have a crucial impact on the diffusion signal and modeling (Nilsson et al., 2012; Andersson et al., 2020; Brabec et al., 2020; Lee et al., 2020; Winther et al., 2023), and should therefore be incorporated into our simulations to improve the realism.
Two primary approaches have been taken to generate realistic numerical white matter phantoms: segmentation (both semiautomatic and automatic) from 3D histology of tissue (Abdollahzadeh et al., 2019; Lee et al., 2019, 2021; Andersson et al., 2020), and numerical synthesis (Balls and Frank, 2009; Hall and Alexander, 2009; Budde and Frank, 2010; Landman et al., 2010; Mingasson et al., 2017; Ginsburger et al., 2019; Callaghan et al., 2020; Villarreal-Haro et al., 2023). Segmentation of white matter tissue provides a very high degree of realism. However, it can be very resource-consuming with respect to time for manual editing and the sacrifice of animal lives. Furthermore, this approach provides little flexibility in the morphological variation of the tissue and only provides static snapshots thereof. In contrast, numerical synthesis allows for much lower resource consumption and allows for a high degree of morphological flexibility. However, the outputs are based on assumptions of what the anatomy looks like (Dyrby et al., 2018).
Various tools have been developed for numerical synthesis of white matter phantoms with complex morphological properties. Recent tools include MEDUSA (Ginsburger et al., 2019), ConFiG (Callaghan et al., 2020), and CACTUS (Villarreal-Haro et al., 2023). MEDUSA (Ginsburger et al., 2019) enables the representation of the most diverse tissue elements by allowing multiple compartments including axons, astrocytes, oligodendrocytes, nodes of Ranvier, and myelinated axons. All structures are represented as spheres. While the sphere representation allows for high representational power of the longitudinal axon morphology characteristics, it does not allow for eccentric cross-sections documented by histology (Abdollahzadeh et al., 2019; Lee et al., 2019; Andersson et al., 2020). Meanwhile, both ConFiG (Callaghan et al., 2020) and CACTUS (Villarreal-Haro et al., 2023) allow only for the inclusion of myelinated axons. However, due to a higher refinement of the axonal cross-sections, these possess higher realism compared with the otherwise circular cross-sections. CACTUS (Villarreal-Haro et al., 2023) stands out for its superior computational efficiency, which in turn enables the creation of larger and more dense phantoms. However, none of these tools considers the dynamic aspects of white matter tissue which has a crucial influence on axon morphology (Andersson et al., 2020). In this work, we present the White Matter Generator (WMG); a new tool for generating interactive numerical phantoms for Monte Carlo dMRI simulations. The interactivity of the WMG tool enables the mimicking of brain white matter dynamics. The phantoms can consist of multiple compartments: unmyelinated axons, myelinated axons, (here defined as fibers), and cells, separated by extra-cellular space. The key assumption for the synthesis is that axon morphology is modulated by the local environment, as observed with XNH imaging in our previous work (Andersson et al., 2020, 2022). Due to morphological flexibility and computational advantages during the optimization, the tool uses ellipsoids as building blocks for all structures during the synthesis; chains of ellipsoids for fibers, and individual ellipsoids for cells. Thereby, fibers can obtain non-circular cross-sections, longitudinal diameter variations, and tortuosity as observed in 3D histology. To mimic a dynamic tissue environment, the tool allows the user to generate phantoms at consecutive time points by interactively changing parameters and tissue composition during the optimization process. The output is in the format of PLY surface meshes, which makes them directly compatible with existing Monte Carlo diffusion simulators such as the widely used MC-DC Simulator (Rafael-Patino et al., 2020) and Camino (Hall and Alexander, 2009). We demonstrate examples of various tissue configurations: varying degrees of fiber dispersion, types of bundle crossings, demyelination, inclusion of static cells, and cell dynamics. The biological relevance of the outputted axons is evaluated based on a set of morphological metrics and compared with those observed with XNH imaging of monkey brain white matter in our previous work (Andersson et al., 2020, 2022).
2 MethodsPhantoms can consist of myelinated axons, axons, and cells, separated by extra-cellular space. To obtain morphological flexibility and computational advantages during the optimization, the tool uses ellipsoids as the building blocks for all structures during the synthesis; chains of ellipsoids for fibers, and individual ellipsoids for cells.
The optimization is based on a force-biased packing algorithm, first introduced by Altendorf and Jeulin (2011), where the phantoms are obtained as an equilibrium between repulsion forces (for avoiding overlap between individual axons and cells) and recover forces (for ensuring the structure of the individual axons) between the ellipsoidal building blocks.
Different brain regions and types of cell dynamics can be mimicked by adapting the configuration w.r.t. fiber diameter distributions, fiber volume fractions (FVF), cell volume fractions (CVF), global dispersion (ϵ), bundle crossings, and interactive changes. Changes to the configuration can be made interactively and at any time during the optimization.
An optimization starts with one configuration file (config-file) and ends with another updated config-file. Thereby, the updated config file can be easily adapted and given as input for another round of optimization according to these adaptations. A conceptual flow chart is seen in Figure 1, and each compartment is described in more detail later in this section.

Figure 1. The WMG tool can be divided into four compartments. Configuration: A config-file is generated based on a set of phantom parameters and optimization parameters. Within the config-file, all structures are represented by ellipsoids. Optimization: The optimization runs based on the config-file, and is carried out by iterating over the axonal ellipsoids. Cellular ellipsoids remain static. Maintaining consistency between the input and output format makes interactive adaptation of the configuration convenient. Re-configuration: After a round of optimization, the config-file can be adapted by changing phantom parameters (e.g., CVF and cell positions), and/or optimization parameters (e.g.,ellipsoidDensity, growSpeed and maxIterations). It can then be used as input for another round of optimization. Post-processing: After a round of optimization, the config-file can be post-processed to obtain a mesh-representation from the ellipsoid-representation. Furthermore, it is often beneficial to perform a Garland Heckbert simplification of these meshes to remove redundant vertices to reduce the computational load of e.g., Monte Carlo diffusion simulations.
The WMG tool is written in TypeScript, whereas supporting functions for configuration and post-processing are written in Python 3. A simplified version of the WMG tool is available as a graphical web interface at https://map-science.github.io/WhiteMatterGenerator. This version allows one to get a more intuitive feeling of the tool and its parameters while testing out different configurations. The full version is available as a command line interface which can be installed by following the instructions at https://map-science.github.io/WhiteMatterGenerator/help/cli. This version enables automation and large-scale production, and this is the version we will be focusing on here. The supporting functions for configuration and post-processing are available at https://github.com/MaP-science/WhiteMatterGenerator.
2.1 ConfigurationThere are two types of parameters: phantom parameters, which specify the content and limits of the phantom, and optimization parameters, which specify the optimization criteria of the phantom. As long as the config-file follows the correct formatting, the user can configure the phantom in any way they like. Below is a guide to the options provided with the WMG.
The phantom parameters are:
• Voxel:
- Outer (larger) voxel dimensions: Defines the spatial restriction of phantom content as a cuboid.
- Inner (smaller) voxel dimensions: Defines the cuboid volume wherein the FVF is optimized and represents the field-of-view of the phantom. This voxel is necessary because the discontinuation at the outer voxel boundary will lead to biased morphology at that boundary.
• Fibers:
- Initial base point (b) and direction (r): fibers are initialized as chains of ellipsoids arranged in straight lines defined with a direction and one fixed base point. The fixed points are uniformly distributed along the axis of primary fiber-orientation .
- Global fiber dispersion (ϵ): fiber directions are uniformly sampled on the surface of a spherical cone, where the height of the cone cap is scaled by ϵ. ϵ = 0.0 allows disperson of 0 deg and ϵ = 1.0 allows dispersion of 90 deg.
- Crossing bundles: Can be configured either as adjacent sheets (Kjer et al., 2023) or interwoven (see Figure 5). Specified by the number of bundles, their primary direction and the fraction of fibers they contain.
- fiber-ellipsoid separation (mapFromMaxDiameterToEllipsoidSeparation): The ellipsoid separation within each fiber is defined from a user-specified mapping function which takes the maximum allowed fiber-diameter as input.
- Allowed diameter ranges for the individual fibers (mapFromMaxDiameterToMinDiameter): To enable closer packing of the axons, it is possible to allow the diameter of each ellipsoid to vary. The range is defined by a user-specified mapping function which takes the maximum allowed fiber-diameter as input. We set the allowed diameter range of the individual axon as a margin around its targeted diameter. The targeted diameters come from an idealized packing of straight parallel cylinders with diameters that follow the targeted gamma-distribution. This initial packing is obtained with the CylinderGammaDistribution() function of the MC-DC Simulator (Rafael-Patino et al., 2020). By initializing all fibers with a diameter which is significantly lower than that of the idealized packing, the axons are able to move more freely during the initial iterations of the optimizations and thereby achieve a more dense packing.
- g-ratio: When the ellipsoid-representation is converted to the mesh-representation the fiber is compartmentalized into axon and myelin based on this g-ratio. That is, the myelin diameter matches that of the fiber, while the axon diameter is scaled in relation to the fiber's diameter through the g-ratio.
- Contract speed (contractSpeed): How much the fibers contract per step, i.e., how stiff the axons are. This number should be ≥0.
- Deformation factor (mapFromDiameterToDeformationFactor): How much the fiber-ellipsoids should deform (change diameter and eccentricity) as opposed to change position when a collision occurs. The deformation is a number between 0 and 1, and is defined by a user-specified mapping function which takes the current fiber-diameter as input. A deformation factor of 0 means that the axonal ellipsoid cannot be deformed at all and hence remains as is. A deformation factor of 1 means that the ellipsoid will deform as much as possible rather than change the position of its center. By adjusting this map between stages of an optimization scheme, the diameters and cross-sections of axons can be fixed such that only the axon trajectories will adapt according to later cell mobility.
• Cells:
- Target CVF (targetCVF): Cells can be added based on ellipsoidal dimensions randomly sampled from normal distributions. One cell is sampled and placed at a time. Cells are added until the targetCVF is met. When placed, a cell may overlap with axons but not cells. In the following optimization, the axons will then adapt to avoid any overlap.
- Position: Defines the center of the cell.
- Shape: Specifies the 3 × 3 transformation matrix used when going from a unit sphere to an ellipsoid. This ellipsoid will be the shape of the cell.
• Output format:
- Radial resolution of outputted meshes: Determines how detailed the output mesh will be.
- Extend fibers around the voxel: Defines whether or not to extend the fibers around the voxel to create mirrored intra-axonal compartments.
The optimization parameters are:
• Target FVF (targetFVF): The targeted FVF.
• Grow speed (growSpeed): How much the fibers grow per optimization step. 0 means no growth, and 1 means that the axon will grow to 100% of its target size in 1 step.
• Maximum number of iterations (maxIterations): Even if the targetFVF is not reached at this point, the optimization will terminate here.
• Output interval (outputInterval): Interval with which an output with the current configuration is provided.
It is beneficial to apply optimization schemes that start out with higher growSpeed (bigger steps) and lower intra-fiber ellipsoid density (less computationally demanding), and go toward lower growSpeed (smaller steps) and higher intra-fiber ellipsoid resolution (more computationally demanding). An example is illustrated in Figure 2. Furthermore, it is crucial to choose realistic parameters to obtain a successful phantom optimization.
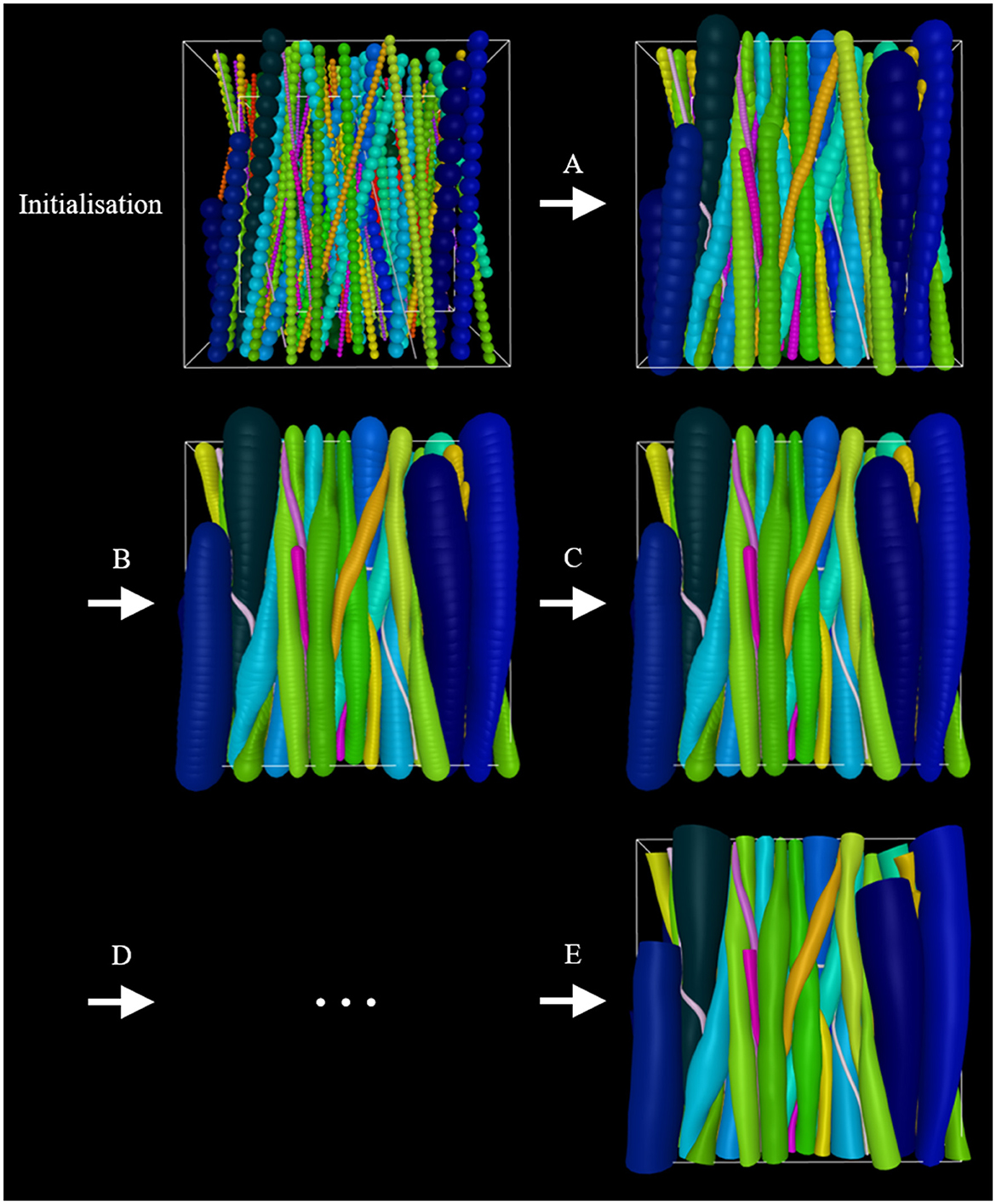
Figure 2. Example of an optimization scheme. At initialization, the phantom consists of an outer-voxel (for spatial restriction), an inner voxel (for the computing optimization metric FVF), straight fibers, and cells. Initially, smaller diameters are assigned to the fibers to allow for more flexibility as they grow into their converged morphology. (A) Inter-fiber ellipsoids grow step-wise toward their maximum allowed diameter while adapting to their surroundings as a consequence of collisions with these. (B) The fiber-ellipsoid density is increased. (C) Growth is repeated. (D) Steps (B) and (C) or variations thereof can be repeated. (E) Once optimized to the user's liking, the ellipsoid-representation can be converted to a mesh-representation and then applied in e.g., Monte Carlo diffusion simulations.
2.2 Optimization 2.2.1 Initialization of voxels, fibers, and cellsEach fiber is initialized with a base point, b, and a direction, r. A ray is traced along r and −r until the voxel boundary is hit. The two points hit by the ray define the endpoints of the fiber. The straight line connecting the two endpoints is then filled with ellipsoids according to the specified ellipsoid density and minimum fiber diameter. Each cell is represented by a single ellipsoid. They cannot move or deform, but otherwise act in the same way as fibers.
Each ellipsoid has two properties: a position vector and a shape matrix. With no deformation, the shape of an ellipsoid is a unit sphere S2 = . The deformation of the sphere is represented by a 3 × 3 matrix, S, such that the surface of the resulting ellipsoid is E = where p is the position.
Initially, the matrix S = μI where μ is given by the allowed minimum radius for the given fiber. For increased flexibility, μ should be very small relative to the voxel size.
Hence, each ellipsoid, j, on each fiber, i, is represented by a position vector, pi, j, and a shape matrix, Si, j, and the surface of the ellipsoid is thus defined by
Ellipsoids are deformed by applying a deformation matrix D = srrT +I . Multiplying (the points on) a surface by D thereby results in a scaling of 1 + s along r where s ∈ ℝ and r ∈ ℝ3, ||r|| = 1. This can be seen by taking an arbitrary point p and transforming it using D
Dp=(srrT+I)p=s(rrT)p+p=s(rTp)r+p. (2)After n deformations of an ellipsoid the shape matrix will have the form S = Dn...D2D1.
2.2.2 Growth, contraction, and redistribution for fiber-ellipsoidsThe growth step considers each ellipsoid j of each fiber i. The shape matrix of the updated ellipsoid Snew is set to a weighted average between the current shape Sold and the target shape (i.e., a sphere having the maximum radius rmax) by
Snew=(1-a)Sold+armaxI (3)where a ∈ [0, 1] is the growSpeed.
A contraction step adjusts the curve on which the ellipsoids lie. The force along the fiber is dependent on the contraction coefficient κ. A value of κ = 0 will do nothing, and a value of κ = 1 will move the position pi, j of the ellipsoid all the way over to c=12(pi,j-1+pi,j+1) making this segment of the fiber a straight line. For any value of κ∈[0, 1] the position is updated to (1−κ)pi, j+κc.
A redistribution step is then performed to prevent ellipsoids from clumping together and thereby creating gaps in the ellipsoid chain. This is done by updating the position of each ellipsoid in a chain such that they are evenly distributed along the trajectory of the fiber. Furthermore, the endpoints of the fibers are moved to the nearest side whenever they are inside the voxel to make sure that the fiber spans the entire voxel.
2.2.3 Collisions: fiber-voxel, fiber-fiber, and fiber-cellFiber-voxel collisions (outer voxel) are checked for each ellipsoid independently. Whenever an ellipsoid's center is outside of the voxel it is projected back onto the boundary. fiber-fiber collisions are checked by computing the potential overlap between each ellipsoid of a fiber and all other ellipsoids of all other fibers. fiber-cell collisions are checked by likewise computing the potential overlap between each ellipsoid of a fiber and all cells.
To compute overlaps between ellipsoids (see Figure 3), we utilize that finding the surface point of an ellipsoid furthest away along a vector r is the same as finding the surface point which has the normal r. When deforming an ellipsoid using the matrix D, the normals are transformed by D−1. Since after n deformations Di, i ∈ the shape has the form S = Dn...D2D1, the corresponding transformation matrix N for the normals is
N=Dn-1...D2-1D1-1=((DnT...D2TD1T)T)-1=((Dn...D2D1)T)-1=(ST)-1 (4)since each Di is symmetric. When going from a normal on an ellipsoid to the corresponding normal of the original sphere, the normal should be transformed by the inverse, i.e., N−1 = ST. After this transformation, the resulting vector can be normalized. Since we now have a unit normal on a unit sphere, the position on that sphere is given by the same vector. To get the corresponding position on the ellipsoid, one can simply multiply by S. Hence the point with the normal r on the ellipsoid with shape S and center at the origin is x(r)=SSTr||STr||. Given the ellipsoid j of fiber i and a direction r the extremal point is thus ei, j(r) = pi, j + xi, j(r). This extremum is used to compute the overlap between two ellipsoids.
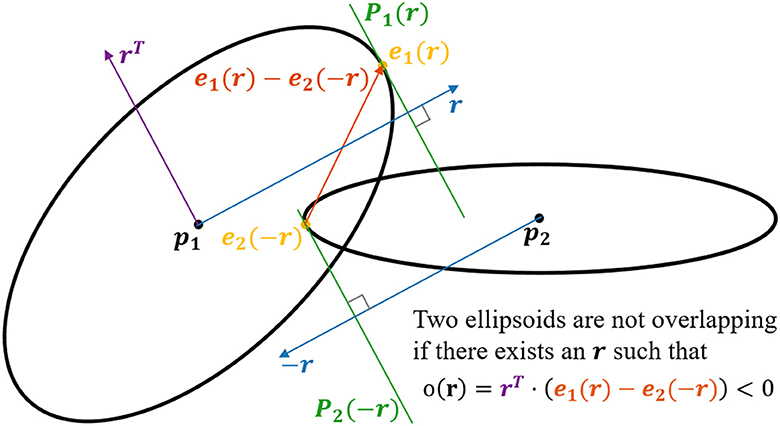
Figure 3. 2D visualization of the concept applied for checking for potential overlap of two ellipsoids. In the example, we have two ellipsoids centered at p1 and p2, respectively. The objective is to check if there exists a set of hyperplanes, P1(r) and P2(−r), which separates the ellipsoids. This is done by finding the surface point e1(r) for which the normal is parallel with r, and the surface point e2(−r) for which the normal is parallel with −r. Now, if the dot product between the vector rT [lying in the plane P1(r)] and the vector e1(r) − e2(−r) is <0, the planes P1(r) and P2(−r) must separate the two ellipsoids. i.e., if there exists an r such that rT · (e1(r) − e2(−r)) < 0, the two ellipsoids are not overlapping.
Define the overlap of two ellipsoids j1 and j2 belonging to the fibers i1 and i2 respectively along an axis r as o(i1, j1), (i2, j2)(r)=rT(ei1,j1(r)-ei2,j2(-r)). If one can find a separating axis (Gottschalk et al., 1997), r, such that o(i1, j1), (i2, j2)(r) < 0, the ellipsoids do not overlap. If o(i1, j1), (i2, j2)(r) > 0 for all values of r, the ellipsoids overlap, since they are convex. To check whether two ellipsoids overlap, one can find the minimum overlap and check if it is positive or negative. The ellipsoids overlap if and only if minro(i1,j1),(i2,j2)(r)>0. The minimum is computed numerically starting with the initial guess r = pi2, j2 − pi1, j1.
When the axis r providing the least overlap o(i1, j1), (i2, j2)(r) is found, it is checked if o(i1, j1), (i2, j2)(r) < 0. If so, nothing should be done. In the case where o(i1, j1), (i2, j2)(r) > 0 the ellipsoids should be updated such that the new value of o(i1, j1), (i2, j2)(r) is 0. This is done by updating both the positions and shapes of the ellipsoids depending on the deformation factor. In practice, a small constant is added to o to make sure that there is a minimum distance between fibers in order to avoid overlaps in the final mesh-representation.
The overlaps are computed at each iteration of the algorithm. In most cases, the overlap will be negative since most ellipsoids are far apart. To avoid the need for computing the overlap between all pairs of ellipsoids, a hierarchy of axis-aligned bounding boxes (AABB) is computed for each axon. If the AABBs of two axons do not overlap, then the overlap computation of all the pairs of ellipsoids between these two axons can be skipped. If the AABBs do overlap, the AABBs will be recursively split into smaller AABBs and checked for overlap until the bottom of the hierarchy is reached. In this case, the ellipsoid overlap is computed.
2.2.4 Updating shapes and positions of fiber-ellipsoidsThe key assumption, that axon morphology is influenced by the local environment (Andersson et al., 2020, 2022), is implemented by requiring each axonal ellipsoid to adapt both shape and position according to its local environment in order to avoid overlapping structures. Each ellipsoid will have a specified deformation factor δ(||xi, j(r)||) ∈ [0, 1] depending on the specified deformation factor map. Each fiber has a minimum allowed radius μi specifying that it should hold for any ellipsoid j that ||xi, j(r)|| ≥ μi. The overlap o(i1, j1), (i2, j2)(r) is divided in two equally big parts, and each part is handled by each of the two ellipsoids. So the deformation of an ellipsoid will result in a decrease in its size of at most 12o(i1,j1),(i2,j2)(r). This will ensure that the ellipsoids will not have a negative overlap after being deformed. Since multiplying by a deformation matrix corresponds to a scaling along r, the distance that the extremal point should be moved has to be divided by the current size along r to get the scaling factor s. So in the case with ellipsoid j1 of fiber i1 the value of s would be s1=-δ(||xi1,j1(r)||)12o(i1,j1),(i2,j2)(r)||xi1,j1(r)||=-δ(||xi1,j1(r)||)o(i1,j1),(i2,j2)(r)2||xi1,j1(r)||. In the case where this deformation would make the ellipsoid's size smaller than the minimum μi, a less negative value of s is chosen such that the resulting size is exactly μi: s2=μi-||xi1,j1(r)||||xi1,j1(r)||=μi||xi1,j1(r)||-1. So the resulting value of s is s = max(s1, s2). So the deformation matrix D1 for ellipsoid j1 is D1=max(s1,s2)rrT+I. Now the shape matrix can be updated by calculating D1Si1, j1. The equivalent computations are performed for ellipsoid j2.
Secondly, the positions of the ellipsoids are updated. Each ellipsoid is treated as if they had equal “mass”, i.e., the center of their positions is conserved. The total distance to move the ellipsoids apart is equal to the overlap o(i1, j1), (i2, j2)(r) after the shapes have been updated. By moving the two ellipsoids by the same amount, the new positions are updated to pil,jl+(-1)l12o(i1,j1),(i2,j2)(r)r for l ∈ .
2.2.5 Computational complexityIn the worst case, all ellipsoids are close to each other and the number of overlaps that need to be computed will be O(ellipsoidCount2). Since the number of ellipsoids is proportional to (1) the number of axons, (2) the voxel size, and (3) the ellipsoid density, this could also be written as O((axonCount·voxelSize·ellipsoidDensity)2).
2.3 Post-processingA phantom is outputted in two formats: an ellipsoid-representation and a mesh-representation. The ellipsoid-representation is the updated config-file where the shape and position of each ellipsoid is specified. This config-file can be edited and used as input for further optimization. The mesh-representation is acquired from the ellipsoid-representation by generating tube-like mesh-segments to connect all ellipsoidal cross-sections within a fiber. The user specifies the number of radial segments that the tubes should have (radial resolution). The number of longitudinal segments is equal to the number of ellipsoids on the fiber. The cells are exported as they are—i.e., meshes having the shape of the corresponding ellipsoids. The mesh-representation can be outputted as individual files for each fiber and cell, or as one combined file containing all elements.
2.3.1 Optimization of meshes for Monte Carlo diffusion simulationsThe higher the ellipsoid-density, the smaller deviation is reached between the ellipsoid-representation and the mesh-representation due to gaps between ellipsoids. Hence, a high ellipsoid density is required to avoid overlapping fibers after conversion to the mesh-representation. This means that the resulting meshes have a likewise high longitudinal resolution. Especially if the meshes are intended for Monte Carlo simulations of dMRI, this is unfavorable since each mesh element comes with a computational cost due to the extensive collision-detection involved. Meanwhile, the high mesh resolution is often redundant.
By performing Garland Heckbert simplification (Garland and Heckbert, 1997) of each myelin and axon mesh, we reduce the number of faces and vertices significantly. The reduction depends on the initial resolution and the allowed deviation between the initial and the simplified mesh. We allow a deviation of minDistance/2 − 0.0005 μm, where minDistance is the minimum distance allowed between ellipsoids of different fibers. For a radial resolution of 16 segments and ellipsoidDensityScaler of 0.20, the Garland Heckbert simplification decreases the number of faces by around 50%.
Before employing the phantoms in Monte Carlo diffusion simulations, the ends of the meshes are sealed to obtain “water tightness”.
The intra-axonal compartment can be extended by making two extra copies of the ellipsoids mirrored through each of the fiber's endpoints without the requirement of further optimization.
2.4 Morphological analysisTo demonstrate the biological relevance of the morphological features expressed in the numerical phantoms generated with the WMG, we compare the morphology of a set of numerical phantoms with real axons. The real axons originate from a monkey brain, and have been quantified by segmentation from XNH-volumes in previous work (Andersson et al., 2020). A total of 58 axons with lengths between 120 and 304 μm were segmented. The meshes are available at www.drcmr.dk/powder-averaging-dataset. The morphological metrics quantify axon diameter variations, cross-sectional eccentricity, and tortuosity. All metrics are sampled with ~375 nm spacing along axon trajectories (some variation due to tortuosity).
2.4.1 Axon diametersWe quantify axon diameter (AD) by the equivalent diameter as in Abdollahzadeh et al. (2019). i.e., axon diameters reported here are the diameter of a circle with an area equal to that of the axonal cross-section perpendicular to its local trajectory. For the real axons, the metric is extracted from the segmentation. This method is described in more detail in Andersson et al. (2020). For the WMG-generated axons, the metric is extracted from the ellipsoid-representation.
For individual axons, mean AD [mean(AD)] is calculated over all measurements along an axon, and the standard deviation of the AD [std(AD)] quantifies the variation of these values.
2.4.2 Cross-sectional eccentricityWe quantify cross-sectional eccentricity based on elliptic parameterization by e=1-b2/a2 where a is the major axis and b is the minor axis (see Figure 10). For the real axons, the circumference of the segmentation is sampled by 24 points. The length of the major and minor axes of a corresponding ellipse is then extracted by fitting a Principal Component Analysis to the sampled points. The results depend on the resolution and smoothing of the images. For the WMG-generated axons, the lengths of the major and minor axes are extracted directly from the ellipsoids.
For individual axons, mean eccentricity [mean (eccentricity)] is calculated over all measurements along an axon, while the standard deviation of the eccentricity [std (eccentricity)] quantifies the variation of these values.
2.4.3 TortuosityWe quantify tortuosity based on the tortuosity factor and the maximum deviation. The tortuosity factor is given as the ratio between the geodesic length of the centerline of an axon, and the Euclidean length between the end points of the centerline (see Figure 11). The maximum deviation is given by the maximum Euclidean distance between the centerline and a straight line spanning the endpoints of the centerline when measured perpendicular to the straight line (see Figure 11).
2.5 Phantoms presented hereAll phantoms included in this paper, are generated based on the optimization scheme shown in Table 1.
留言 (0)