1 Introduction

Environmental perturbations, such as thermal stress and disease challenges, are major threats to livestock production (Lacetera, 2019). In this context, breeding more resilient animals, i.e., animals that can better cope with changing environments, has been indicated as an alternative to improve animal welfare and productivity in challenging environments (Brito et al., 2020). Genetic selection for more resilient animals using linear mixed model equations considering additive genetic effects has been in development (Tiezzi et al., 2020; Freitas et al., 2023). However, there are other non-genetic effects that may play a role in heritable variation, including microbial, cultural, and epigenetic effects (David and Ricard, 2019).

The field of epigenetics has received more attention during the past decade due to its potential to help uncover the phenotypic variation and inheritance of complex traits. However, the epigenetic term is not novel, and it was first defined in 1940s by Conrad Waddington (Waddington, 1942a; Waddington, 1942b), even before the DNA structure was known. Waddington’s first definition of epigenetics was associated with “phenotypic changes without changes in genotypes” (Waddington, 1942a; Waddington, 1942b). Nowadays, epigenetics can be defined as “the inheritance of gene expression patterns without altering the underlying DNA sequence” (Allis and Jenuwein, 2016). The epigenome is mainly composed by DNA methylations, histone modifications, chromatin remodeling, and non-coding RNA (Bird, 2002; Morris and Mattick, 2014), and can dynamically change due to a variety of external factors (exome), such as nutrition (pre- and post-natal), stress (e.g., heat, behavioral, disease), and exposure to chemicals (e.g., therapeutical drugs and toxic pollutants) or pathogens (Ibeagha-Awemu and Yu, 2021). As reviewed by Wang and Ibeagha-Awemu et al. (2021) and Ibeagha-Awemu and Yu (2021), epigenetic markers can affect various economically important traits in livestock. Therefore, it is important to investigate the amount of phenotypic variation of complex traits that can be explained by epigenetics and how this information could be used for management and breeding purposes.

Epigenetic marks are created during environmental stress and can be passed to the offspring by the germ cells and can, consequently, affect phenotypic variation in subsequent generations (Tal et al., 2010; Heard and Martienssen, 2014). Usually, epigenetic markers acquired during life by an individual would be removed during meiosis and germline reprogramming so that the embryos in the next-generation would develop based on genetic information without influence of past environment (Ibeagha-Awemu and Yu, 2021). Beyond environmental factors, epigenetic markers can be affected by intrinsic factors, such as sex and age (Wang and Ibeagha-Awemu, 2021). When the epigenic mark reset fails, some epigenetic marks are inherited and can affect the next generations (Heard and Martienssen, 2014). Intergenerational epigenetic effects can impact phenotypic variation up to two generations on the dam side or one generation on the sire side after exposure to the stressors, while transgenerational epigenetic effects influence phenotypic variability in further generations even without additional environmental stressors, when they can remain or be lost (Heard and Martienssen, 2014).

Recent studies have aimed to model the effect of stressors (e.g., heat stress) on future performance and next generations in genetic evaluations to capture epigenetic effects (Kipp et al., 2021; Weller et al., 2021). For instance, Kipp et al. (2021) used random regression models with Legendre orthogonal polynomials to model time-lagged temperature humidity index (THI) experienced by dairy cattle animals during the last week before birth (pre-natal or in uterus heat stress) in a genetic model. Weller et al. (2021) tested the hypothesis of transmission of transgenerational heat stress effects by evaluating the effect of the exposure of F0 (great grandmother) dairy cows during pregnancy over a F3 (great-granddaughter) generation of cows. These studies used indirect approaches to determine the effect of stressors on the phenotypic variation of animals in an intergenerational (Kipp et al., 2021) and trans-generational way (Weller et al., 2021), i.e., they did not formally include an epigenetic effect in the statistical genetic models.

Previously, Varona et al. (2015) proposed an approach for directly accounting for the transgenerational epigenetic effects in the animal models commonly used for livestock genetic evaluations. The authors proposed to include the transgenerational epigenetic effect as an additional random effect in the animal models, with the inverse of the epigenetic relationship matrix (Λ−1) used as the covariance structure for the epigenetic effect at the individual level. The epigenetic relationship matrix (Λ) and its inverse were derived by Varona et al. (2015) using the theory developed by Tal et al. (2010). The advantages of using the Varona’s et al. (2015) method are: 1) it allows the estimation of the proportion of phenotypic variance explained by the transgenerational epigenetic effects, termed as transgenerational epigenetic heritability; 2) it is an epigenetic effect associated with an overall response to environment/stress instead of only accounting for specific stressors (e.g., heat stress); 3) it provides epigenetic solutions for all animals included in the pedigree file; and, 4) it is based on routinely-recorded datasets as opposed to generating additional datasets such as whole-genome bisulfite sequencing for assessing DNA methylation patterns. However, the method is based on strong assumptions, such as the independence of epigenetic, genetic, and residual effects. Few studies have applied the Varona’s et al. (2015) method in the literature (Varona et al., 2015; Paiva et al., 2018a; Paiva et al., 2018b), and none to our knowledge have used pig datasets. There are well-established reports of lifelong negative postnatal effects of prenatal (in utero) heat stress for production and reproduction traits in pigs (Johnson and Baumgard, 2019), but the effect of epigenetics on phenotypic variation in complex traits in pigs is still unknown. Therefore, the primary study objectives were to estimate transgenerational epigenetic heritability, determine the percentage of the reset and transmissibility rate of epigenetic marks, as well as to estimate genetic parameters and predict breeding values based on statistical models fitting exclusively genetic or genetic and epigenetic effects for growth, body composition, and reproductive traits in North American Landrace pigs.

2 Materials and methods

No ethical and animal care approval was needed for this study because all the data used was previously collected and provided by commercial breeding operations.

2.1 Traits and phenotypic quality control

Datasets from five nucleus herds located in North Carolina and Texas (USA) were provided by Smithfield Premium Genetics (SPG; Rose Hill, NC, United States) and consisted of records from purebred Landrace pigs. Measurements were collected between the years 2014–2019. The five traits included in this study were categorized as: 1) growth: birth weight (BW) and weaning weight (WW); 2) body composition: off-test backfat (BF); and 3) reproduction traits: total number of piglets born (TNB) and number of piglets born alive (NBA).

Records outside of an interval of 3.5 standard deviations (SD) from the mean were removed from further analyses. Observations from animals above the sixth parity or sows with less than 3 or more than 20 piglets per litter were also removed due to lower incidence. Animals with phenotypic observations but not present in the pedigree file and animals whose pedigrees were not complete for at least four generations were also removed from the analyses. This quality control was done to keep only relevant information for the variance component estimation analyses (Nilforooshan and Saavedra-Jiménez, 2020), especially for estimating epigenetic effects that require deeper knowledge of the genealogy and more complex partition of the phenotypic variance (Tal et al., 2010). The “optiSel” package in R (Wellmann, 2019) was used to check for erroneous pedigree entries and pedigree completeness. After the phenotypic data editing, the contemporary groups (CG) were defined by the concatenation of birth year, month, and farm for the growth and body composition traits and farrow year, month, and farm for the reproductive traits. The CG were defined based on the trait groups to better capture animals that would move together and share similar management practices (i.e., contemporaries). The number of animals and the descriptive statistics for all traits, after quality control, as well as the number of CG are included in Table 1. A minimum number of five animals was set for each level of the CG effect as well as for all other fixed effects included in the models (described later).

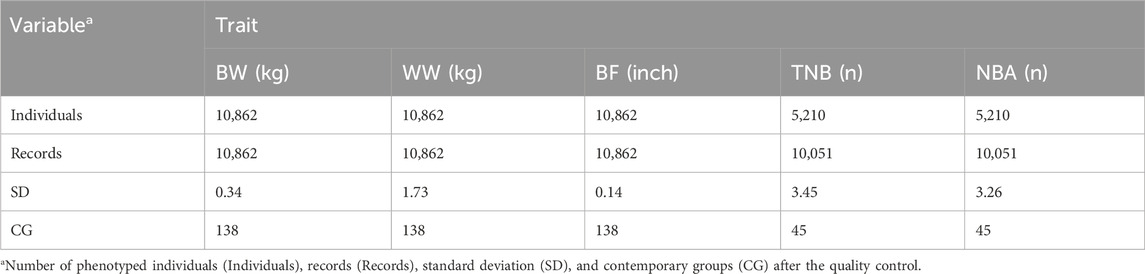
Table 1. Descriptive statistics for birth weight (BW), weaning weight (WW), backfat (BF), total number of piglets born (TNB), and number of piglets born alive (NBA) in North American Landrace pigs.

2.2 Pedigree and genotypes

After pedigree quality control, the pedigree consisted of 17,794 animals, spanning a maximum of 12 generations, with a mean (SD) pedigree completeness index of 0.84 (0.33) for growth and body composition traits, while for reproductive traits, the pedigree comprised 8,390 animals, spanning 11 generations, with a pedigree completeness index of 0.83 (0.29). The “optiSel” package in R (Wellmann, 2019) was also used to calculate the pedigree statistics shown above. The RENUMF90 package from the BLUPF90+ family of programs (Misztal et al., 2018) was used to renumber the pedigree and keep up to four generations back from the animals with phenotypic and/or genomic information to reduce the pedigree and, consequently, time to reach convergence and memory usage during the analyses (Nilforooshan and Saavedra-Jiménez, 2020). Previous analyses tracing up to 20 generations back in the pedigree using RENUMF90 (Misztal et al., 2018) did not affect the estimates (results not shown).

Genotypes were available for 12,759 individuals genotyped with a Porcine SNP50K Bead Chip (Illumina, San Diego, CA, United States). The quality control (QC) was performed using the PREGSF90 software (Misztal et al., 2018) to remove samples and SNPs with call rate lower than 0.90 and SNPs with minor allele frequency lower than 0.05, SNPs with a difference between expected and observed heterozygous greater than 0.15, and SNPs located in non-autosomal chromosomes or with unknown genomic positions. After QC, 12,759 individuals and 34,524 SNPs remained for further analyses.

2.3 Transgenerational epigenetic variance and heritability estimation

The transgenerational epigenetic component of covariance between relatives was derived based on the method proposed by Tal et al. (2010). The main assumption made by the authors was that the covariances between close relatives change when epigenetic marks are being transmitted across generations. Later, Varona et al. (2015) used this theory to derive the Λ and Λ−1. The Λ matrix is calculated using the auto-recursive parameter λ, in which λ=0.51−ν, where ν is the reset coefficient, defined as the probability that the epigenetic state of the genome changes from one generation to the next. In brief, Tal et al. (2010) proposed a reset coefficient (ν) of the epigenetic marks and its complement (1−λ) as the transmissibility of the epigenetic marks, which weights the covariance between relatives in the presence of factors that can cause epigenetic changes. A Python function (see Additional file 1) was implemented to calculate the lower triangular and diagonal portion of Λ−1 directly in the long format to estimate the transgenerational epigenetic component of variance (σξ2) and heritability (hξ2) using the BLUPF90 family programs (Misztal et al., 2018). The Phyton function developed in this study was based on the algorithm proposed by Varona et al. (2015), which assumed the same epigenetic variance across generations and between sexes. These assumptions allow the calculation of the epigenetic heritability (or epigenetic ratio) as hξ2=σξ2^σy2^, where σy2^ is the phenotypic variance, i.e., is the sum of all variance components from the model used to evaluate each trait.

2.4 Statistical methods

Model building was conducted before fitting the epigenetic models. The systematic effects (presented later) were variables statistically significant at 5% probability in a linear model from a set of environmental (non-genetic) variables. Once the systematic effects were defined for each trait, the set of random effects to be used in the genetic models were chosen under the Restricted Maximum Likelihood (REML) (Patterson and Thompson, 1971) approach using the Average Information algorithm (AI-REML) (Gilmour et al., 1995) and the Akaike Information Criterion (AIC) (Akaike, 1974). The rank for the genetic models using different sets of random effects is presented in Supplementary Material 2: Supplementary Table S1, and the best genetic model (lowest AIC with meaningful estimates of the genetic parameters, i.e., within or close to previous estimates for the parameter and trait) for the evaluated traits were:

where Equations 1–3 are the genetic models for the growth (BW and WW), back fat thickness (BF), and reproductive (TNB and NBA) traits, respectively; y is the vector of the phenotypic records for each trait; b is the vector of systematic effects (for BW: gender, birth parity, and CG; WW: gender, birth parity, CG, and weaning age and birth weight as covariates; BF: gender, birth parity, CG, and off-test age as covariate; TNB and NBA: farrowing age as linear and quadratic covariates, CG, and parity); u is the vector of random direct additive genetic effects; m is the vector of random maternal additive genetic effects; q is the vector of random common litter environment effects; pe is the vector of random permanent environmental effects; and e is the vector of random residuals. X, Z, S, and W are the incidence matrices for b, u, m, q, and pe, respectively. BW was used as a covariate in the WW to account for the starting point of the growth trajectory in this trait. The AIREMLF90 software (Misztal et al., 2018) was used to estimate variance components under the following assumptions for each genetic model:

umqe∼N0000,Aσu2Aσu,m00Aσu,mAσm20000Iσq20000Iσe2(4)umqe∼N0000,Aσu20000Aσm20000Iσq20000Iσe2(5)ume∼N000,Aσu2Aσu,m0Aσu,mIσm2000Iσe2(6)upee∼N000,Aσu2000Iσpe2000Iσe2(7)

where the assumption (Equation 4) was used for BW, Equation 5 for WW, Equation 6 for BF, and Equation 7 for TNB and NBA. The pedigree-based relationship matrix (A) was used to model the covariances in u and m in the genetic analysis, and the identity (I) matrix was used for the q, pe, and e. The σu2, σm2, σq2, σpe2, and σe2 are the variance components for u, m, q, pe, and e, respectively, and σu,m is the covariance between u and m. The genetic models, i.e., models using the A as covariance structure for the additive genetic effects, will be called BLUP models from now on.

The A matrix was replaced by the H matrix in the BLUP models when the genomic information was included in the estimation of genomic-based variance components, i.e., single-step genomic BLUP models (ssGBLUP) (Legarra et al., 2009; Christensen and Lund, 2010). This H is the matrix that combines the pedigree and genomic information, and its inverse (H−1) was computed directly as (Aguilar et al., 2010):

H−1=A−1+000ταG+βA22−1−ωA22−1(8)

where A−1, A22, A22−1, and G are the inverse of the pedigree relationship matrix, part of the A related to the genotyped animals, its inverse, and the genomic relationship matrix, respectively (Equation 8). The G was computed as in method 1 proposed by VanRaden (2008). The scaling parameters (τ and ω) were equal to 1.00, and the blending parameters α and β were equal to 0.95 and 0.05, respectively.

The epigenetic model for each trait was obtained by expanding the BLUP models for each trait including the transgenerational epigenetic effect, which will be called Epi-BLUP. In summary, the term Zξ was included in the models (Equations 1–3), which became:

where Equations 9–11 are the epigenetic models for growth (BW and WW), backfat thickness (BF), and reproductive (TNB and NBA) traits, respectively; ξ is the vector of epigenetic effects, with ξ ∼N0,Λσξ2 assumed to be uncorrelated to all the other random effects, as proposed by Tal et al. (2010) and Varona et al. (2015); all the other effects were previously described. To estimate the transgenerational epigenetic heritability, the best epigenetic model, i.e., the model that presented the best λ, was defined first because the reset and transmissibility of the epigenetic markers are population-specific parameters. In this sense, a grid search ranging from 0.05 to 0.45 by 0.05 (totaling nine epigenetic models for each trait) was evaluated for λ in the creation of Λ−1 that was fitted directly in the epigenetic models. The H matrix (Legarra et al., 2009) was also used to model the additive genetic relationships in the epigenetic models to study the impact of genomic information in these models, i.e., epigenetic models including genomic information (Epi-ssGBLUP) and not epigenomic models (e.g., using whole-genome DNA methylation).

2.5 Model comparison

Even though both REML-based and Bayesian inference-based methods should converge to the same population parameters, there are differences in the statistical properties of these methods, which are important to consider, especially if the models are complex (Gianola and Fernando, 1986). In this context, we have estimated variance components based on BLUP, ssGBLUP, Epi-BLUP, and Epi-ssGBLUP models using Bayesian inference. Bayesian inference was used in this step because the epigenetic models have a complex covariance structure and this method is more robust to model complexity (Gianola and Fernando, 1986).

The best Epi-BLUP or Epi-ssGBLUP model for each trait, i.e., with the best λ, under Bayesian inference was chosen using the Deviance Information Criterion (DIC; lower values indicate better model fit) (Spiegelhalter et al., 2002). Maximum likelihood estimates from the AI-REML runs were used as starting values in the Bayesian inference to improve the sampling process (Harms and Roebroeck, 2018) as poor starting values tend to slow model convergence (Raftery and Lewis, 1992). The THRGIBBS1F90 software (Misztal et al., 2018) was used to estimate variance components considering all traits as linear traits. Initial values for size, burnin, and interval in the MCMC chain were defined as 100,000, 10,000, and 10, respectively, for all traits and models, and these values were increased if convergence was not achieved based on the author’s experience and final values are presented in the results section. Convergence was verified based on the Geweke diagnostic (Geweke, 1992) with 5% probability, a stationarity test (Heidelberger and Welch, 1983) criterion, and visual inspection. The convergence tests and visual inspection of the chains were done using the R software (R Language, 2012) with the “boa” package (Smith, 2007).

2.6 Evaluating prediction results

After estimating the variance components, the solutions of the mixed model equations for the best fit models were evaluated. The purposes of these analyses were mainly to: 1) investigate the association between the solutions of the additive, maternal, and permanent environment effects in a genetic or genomic model including the transgenerational epigenetic effects; 2) assess the changes in the solutions by including the transgenerational epigenetic effects; and 3) evaluate the prediction accuracy, bias, and dispersion of the breeding values in young non-phenotyped individuals when including the transgenerational epigenetic effects in the models.

The association between the additive, maternal, and permanent environment effects when including the transgenerational epigenetic effects in the models was evaluated using a Pearson correlation between the solutions considering all animals used for variance component estimation (please see the sections Traits and dataset edits and Pedigree and Genotypes). Changes in the solutions when including the transgenerational epigenetic effects were evaluated using a paired t-test with a significance level of 0.05% for the difference between the solutions, also considering all animals used for variance component estimation.

The prediction accuracy, bias, and dispersion were investigated using the Linear Regression method (LR) (Legarra and Reverter, 2018). In brief, a set of animals born in 2019 (N = 571) chosen among the ones used for the estimation of variance components had their phenotypic records masked for BW, WW, and BF, and were considered as the focal animals (young non-phenotyped selection candidates). In the case of TNB and NBA, the focal animals for the LR method were born in 2017 (N = 933), because this was the last year with phenotyped animals for the reproductive traits. After defining the focal animals, the whole and partial datasets for applying the LR method were created. The whole dataset included all animals and phenotypes used for variance component estimation in the prediction, while in the partial dataset the phenotypes for the focal animals were removed, so that their estimated breeding values (EBV) were obtained based on the relationships with the remaining animals with phenotypic records. In the end, the prediction accuracy, bias, and dispersion of the EBV for the focal animals were calculated as:

Accuracy=covEBVW,EBVI1−F¯σ^u2(12)Bias=aveuEBVI^−aveuEBVW^(13)Dispersion=covEBVW,EBVIvarEBVI−1(14)

where covEBVW,EBVI is the covariance between the EBV in the whole (EBVW) and incomplete, i.e., partial, (EBVI) datasets, F¯ is the average inbreeding (pedigree or genomic), ave represent the arithmetic average function, uEBVW^ and uEBVI^ are the predicted EBV in the whole and incomplete datasets, respectively, and varEBVI is the variance of the EBV in the incomplete datasets (Equations 12–14). The other equation components were previously described.

3 Results3.1 Model comparison

The Epi-BLUP model presented a better fit (lower DIC) compared to BLUP for BW, WW, and BF (Table 2). λ = 0.05 provided the lowest DIC for BW and WW in the Epi-BLUP models (10,387.47 and 44,350.08, respectively), and λ = 0.10 was the best for BF (−30,458.31), which were lower than the DIC of the BLUP models for these traits (21,258.82, 52,803.60, and −17,142.00, respectively). Epi-BLUP models with λ = 0.05 provided slightly lower DIC for TNB and NBA (52,651.09 and 51,609.69, respectively) compared to the BLUP model (52,651.31 and 51,610.34, respectively), suggesting that the Epi-BLUP models would be a better choice for these traits as well.

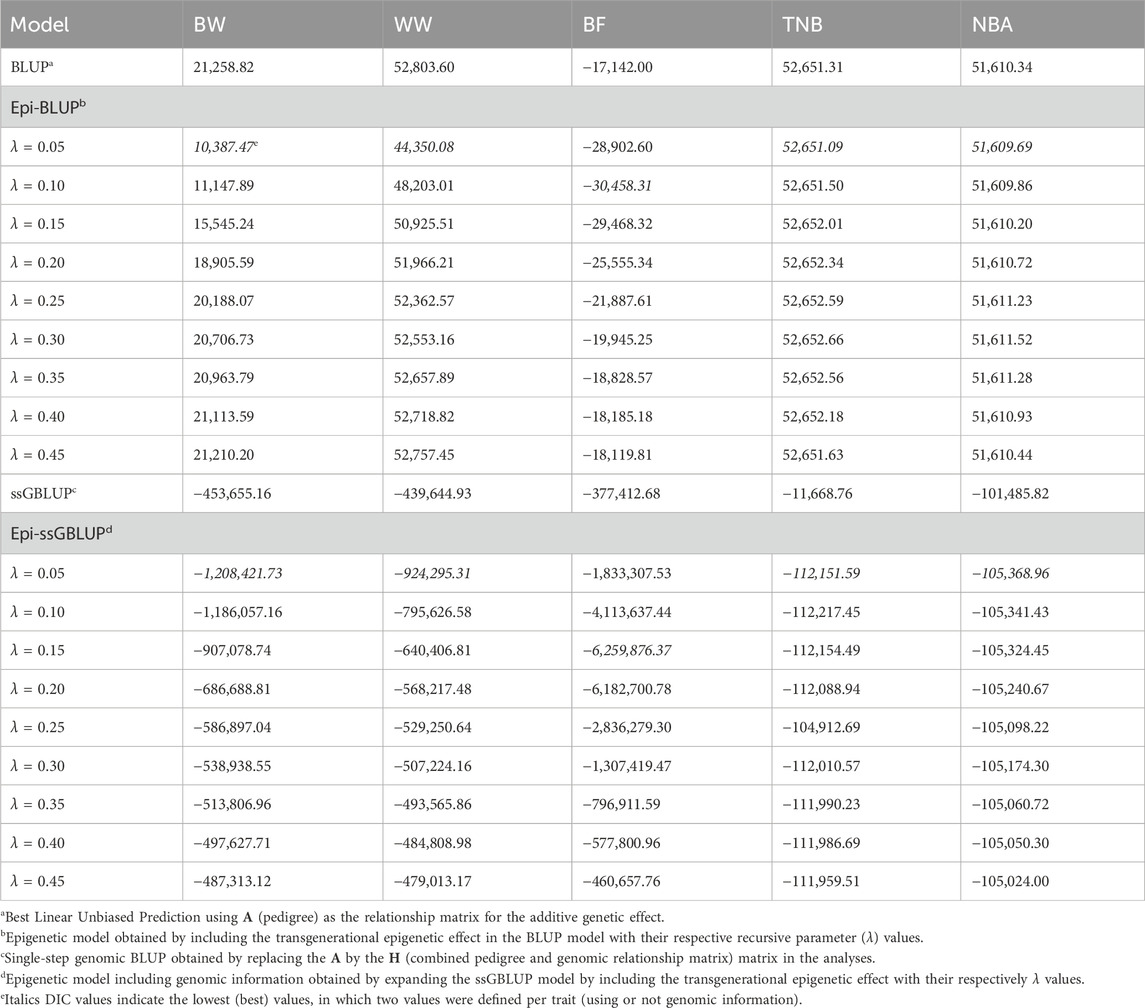
Table 2. Deviance Information Criteria (DIC) of genetic and epigenetic models including or not genomic information in the relationship matrix for birth weight (BW), weaning weight (WW), backfat thickness (BF), total number of piglets born (TNB), and number of piglets born alive (NBA) in North American Landrace pigs.

When including genomic information, DIC values were lower in the best Epi-ssGBLUP models for BW, WW, BF, TNB, and NBA (−1,208,421.73, −924,295.31, −6,259,876.37, −112,151.59, −105,368.96, respectively) compared to the ssGBLUP models for these traits (−453,655.16, −439,644.93, −377,412.68, −11,668.76, −101,485.82, respectively). Similar ranks were observed between the Epi-ssGBLUP and Epi-BLUP models under Bayesian inference, with the best λ value of 0.05 for BW, WW, TNB, and NBA, except for BF, with the best λ value of 0.15.

3.2 Variance components and genetic parameters

The results of the genetic parameter estimation for BW are presented in Table 3. Chain size was much higher in the epigenetic models to obtain stable samples in the Markov-Monte Carlo chain (MCMC). The size of the chain for the Epi-BLUP model (biggest chain) was 1,750,000 samples with a burn-in of 1,000,000 and thin of 100, while for the BLUP model (smallest chain), these parameters were 220,000, 10,000, and 10, respectively. Small to no differences were observed among the variance components and genetic parameters between BLUP, Epi-BLUP, and ssGBLUP for BW, except for σe2^, which was much smaller in the Epi-BLUP model. In this sense, σP2^ was also similar across the BLUP, Epi-BLUP, and ssGBLUP models, indicating that there was a partition of the variances in the Epi-BLUP model which resulted in the σξ2^ being extracted directly from the residuals. In the case of the Epi-ssGBLUP, there was an inflation of the σu2^ and σm2^ compared to the other models, which were more than two and three times larger, respectively, in the Epi-ssGBLUP. Despite the reduction in the proportion of the phenotypic variation explained by the common litter effect (q2) and σξ2^ in the Epi-ssGBLUP model, the σP2^ in this model was the largest compared to all other models for BW (0.766 vs. ∼0.560). The additive direct and maternal heritability estimates followed a similar pattern of the variance components across models, but the q2 and σξ2, and consequently hξ2, were higher in the Epi-BLUP model (0.296, 0.186, and 0.330, respectively) compared to the Epi-ssGBLUP model (0.204, 0.160, and 0.209, respectively). A similar pattern of the results was observed in the WW and BF (Tables 4, 5, respectively).

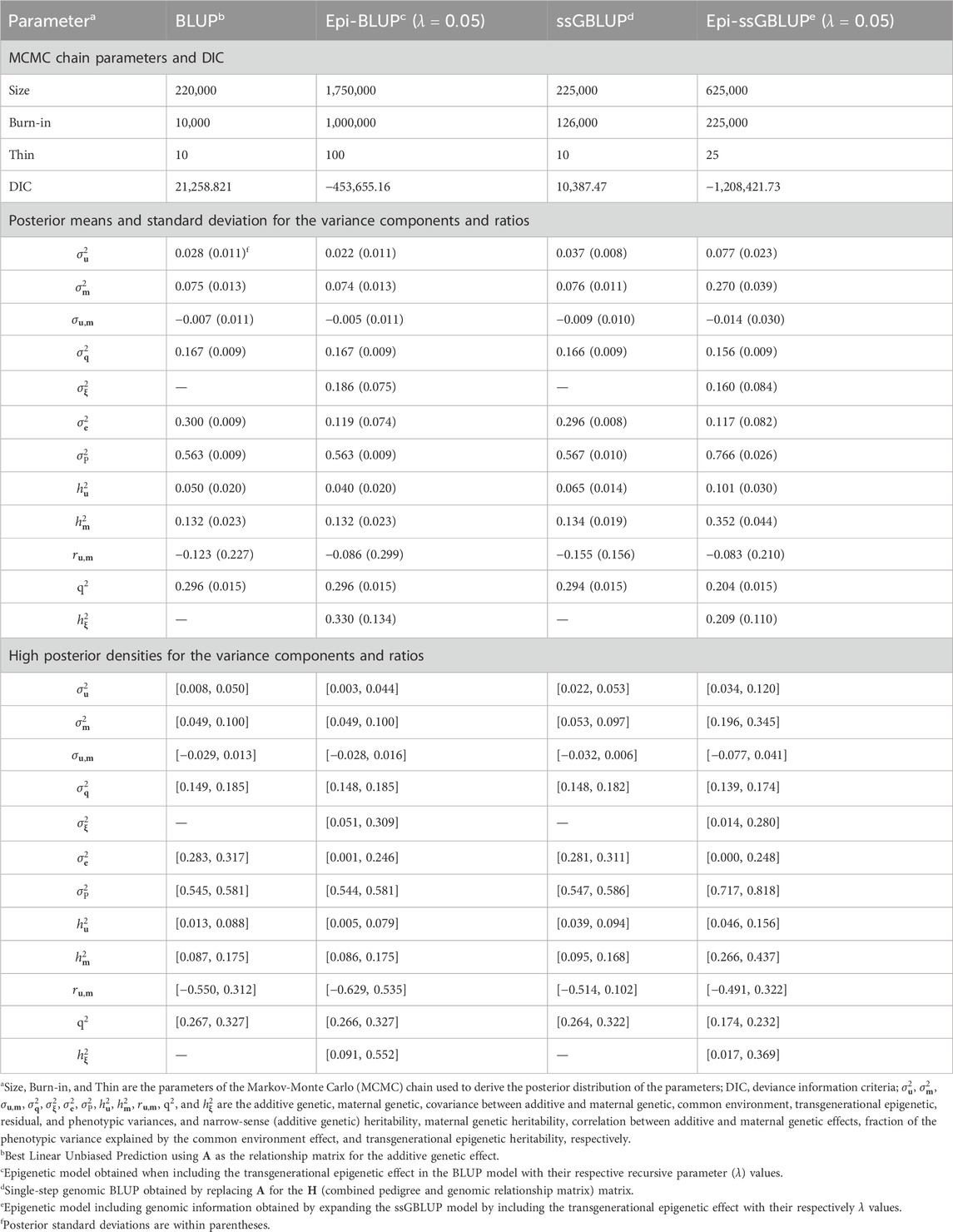
Table 3. Chain parameters, posterior means, and high posterior densities of the variance components and genetic parameters estimates for the birth weight of Landrace pigs using genetic and epigenetic models with pedigree- or single-step genomic BLUP under a Bayesian approach.

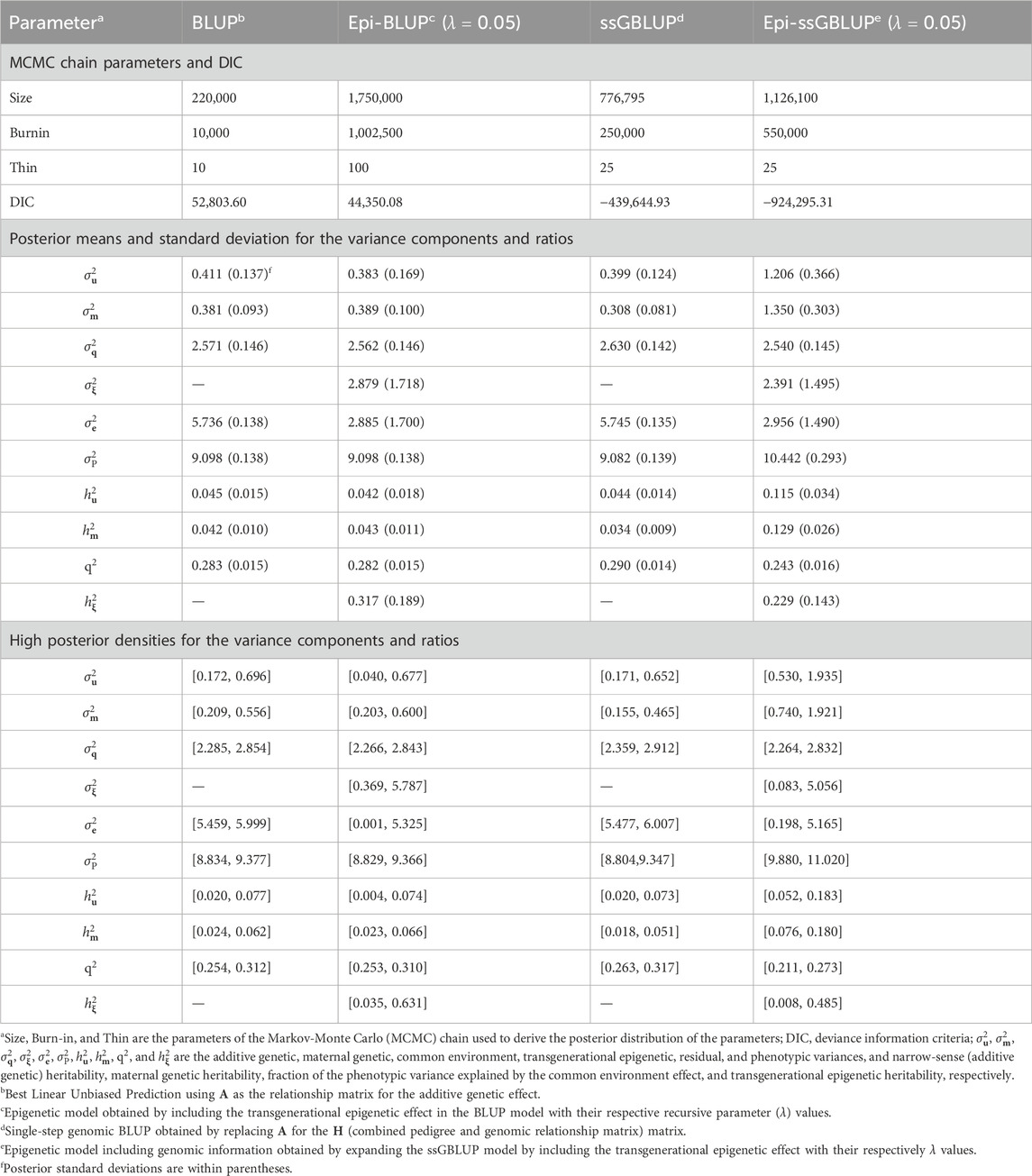
Table 4. Chain parameters, posterior means, and high posterior densities of the variance components and genetic parameters estimates for the weaning weight of Landrace pigs using genetic and epigenetic models with pedigree- or single-step genomic BLUP under a Bayesian approach.

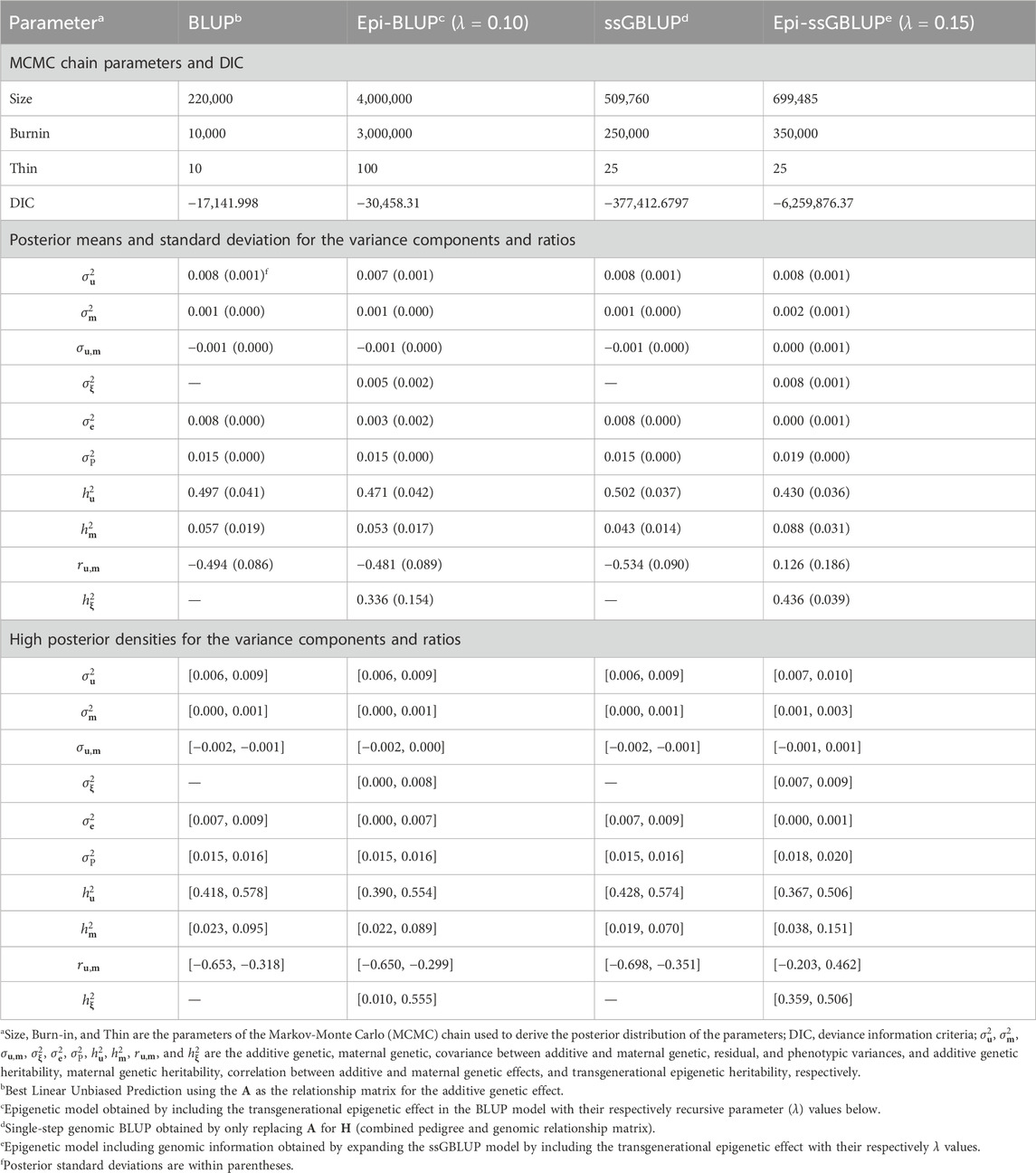
Table 5. Chain parameters, posterior means, and high posterior densities of the variance components and genetic parameters estimates for the backfat of Landrace pigs using genetic and epigenetic models with pedigree- or single-step genomic BLUP under a Bayesian approach.

The results of the MCMC parameters, variance components, and genetic parameters for TNB and NBA are presented in Tables 6, 7, respectively. Similar patterns were observed for the MCMC parameters, σu2^, σP2^, hu2, and hξ2 in the TNB and NBA compared to the growth and body composition traits. However, the source of σξ2^ in the Epi-BLUP and Epi-ssGLUP models was not due to σe2^ but due to the σpe2^ in the reproductive traits. There were no substantial differences in the σe2^ across all models for TNB and NBA. On the other hand, σpe2^ reduced in both Epi-BLUP and Epi-ssGLUP models by the same amount of variance captured by σξ2^ in TNB and NBA. Also, similar to what was observed for growth and body composition traits, the σP2^ was similar to the BLUP, Epi-BLUP, and ssGBLUP estimates, suggesting that there was only repartitioning of variances in the Epi-BLUP compared to BLUP and ssGBLUP. The inflation in the σu2^, σP2^, and hu2 estimates from the Epi-ssGBLUP for the reproductive traits was also noticeable, with 3-fold increases for σu2^ and hu2, and 14% for σP2^ in comparison to the ssGBLUP estimates. The posterior means of the hξ2 for TNB and NBA in the Epi-BLUP (0.044 and 0.042, respectively) and Epi-ssGBLUP (0.033 and 0.032, respectively) were much lower compared to those for BW, WW, and BF (0.330, 0.317, 0.336, respectively, for the Epi-BLUP and 0.436, 0.229, and 0.209 for the Epi-ssGBLUP, respectively).