1 Introduction

The extracellular matrix (ECM) plays a crucial role in development and in disease. For example, the ECM plays a role in cancer cell migration (Najafi et al., 2019; Yamaguchi et al., 2005), wound healing (Maquart and Monboisse, 2014; Diller and Tabor, 2022), and angiogenesis (Stupack and Cheresh, 2002). The ECM is a complex collection of large fibers such as collagen, fibronectin, and other proteins (Theocharis et al., 2016). The orientation of fibers in the ECM plays an important role in tumor vascularization (Balcioglu et al., 2016), mechanical cell–cell communication (Nahum et al., 2023), and blood clot formation (Kim O. V. et al., 2017). The ECM is continuously remodeled by cells both chemically, through the synthesis and degradation of ECM fibers and associated components, and mechanically, by pulling and reorienting fibers (Theocharis et al., 2016; Winkler et al., 2020). As ECM remodeling leads to local changes in ECM properties such as stiffness, structure, density, and isotropy, to which cells respond through changes in adhesion, cell contraction, or pseudopod extension (Reinhart-King et al., 2005; Malandrino et al., 2019; Doyle et al., 2022), there is a bidirectional chemical and mechanical reciprocity between the cells and the ECM. In this work, we focus specifically on the mathematical modeling of mechanical cell–ECM reciprocity in fibrous ECM, in particular the role of ECM isotropy. For mathematical models of other forms of cell–ECM reciprocity, we refer to Daub and Merks (2013); van Oers et al. (2014); Rens and Merks (2017), Rens and Merks (2020); Chiang and Chung (2024).

The present study attempts to provide mechanistic explanations for three behaviors of cells on fibrous matrices: (1) cell spreading as a function of ECM stiffness, (2) alignment of cells to ECM fiber orientation, and (3) a hypothetical role of ECM anisotropy in mechanical cell–ECM reciprocity.

First, certain cell types, such as endothelial cells, fibroblasts, smooth muscle cells, and osteogenic cells, show a monotonic increase in spreading with substrate stiffness. These cells are relatively small on softer substrates, elongate on intermediate substrates, and achieve maximum spreading on highly stiff substrates such as coated glass (Yang et al., 2017). Other cell types, including Jurkat T cells and NIH 3T3 fibroblasts, show a biphasic response of spreading to substrate stiffness, showing maximal cell spreading at an intermediate optimal level of substrate stiffness (Oakes et al., 2018; Wahl et al., 2019; Janmey et al., 2020).

Second, cell alignment is influenced both by the mechanical properties of the fibers and by the cell adhesion properties. In Friedrichs et al. (2007), cells are cultured on a two-dimensional substrate assembled out of thin aligned collagen fibrils. Cells align along the collagen fibrils and bundle parallel fibrils together at their poles and deform the orthogonal fibrils, which creates holes in the substrate. When this experiment was repeated with fragile fibrils, the cell did not elongate, and the fibers surrounding the cell were digested. This suggests that cells require a firm ECM to adhere to and that anisotropic traction force is required to elongate and align to the fibrils. Next, they found that the cell adhesions to the fibrils influence cell alignment. In general, cells adhere to the ECM with integrins, which are membrane-piercing receptors that bind to proteins in the ECM with varying binding strengths, possibly regulated by mechanical tension (Kechagia et al., 2019). Specifically, Friedrichs et al. (2007) found that cells expressing the integrin α2β1 align on the fibrils, whereas cells that did not express this integrin adhered to the fibrils but did not align.

Finally, cells not only respond to cues in the ECM but also reorient the fibers in the ECM. Contractile breast cancer cells deform fibrous collagen and reorient the fibers to point toward themselves. Pairs of these contractile cells create aligned bridges of fibers between them (Kim J. et al., 2017).

Computational modeling is well-suited for providing insights into mechanical cell–ECM reciprocity (Crossley et al., 2024). Before introducing our own approach, we briefly review a selection of specific computational models of cell–ECM reciprocity involving mechanosensitive adhesions and a fibrous ECM. We highlight two factors that are crucial to be included in a computational model of the reciprocity between ECM fiber alignment and cell morphology, namely, (i) cell-induced changes in ECM structure and (ii) ECM-induced changes in cell shape.

We first review computational models focused on ECM mechanics in response to cell contraction (i). Using a 3D finite element (FE) representation of the ECM, Paukner et al. (2023) showed that cell contractility and force-dependent cell–ECM adhesions suffice for guiding cell migration upward stiffness gradients. This model focused on ECM deformation by the cell but could not capture cell shape change due to changes in the ECM because the cell was modeled as a point particle with an adhesive annulus. They concluded that cell contractility, combined with mechanosensitive cell–ECM adhesions, can explain several phenomena in cell migration. In a different study of cell migration, Feng et al. (2019) introduced a simple bead–spring network approximation of a deformable ECM and a migrating ellipsoidal cell. They showed that a torque balance on the mechanosensitive adhesions of the cell causes the cell to orient along fibers, after which the cell starts migrating. In Feng et al. (2019), the cell’s ability to sense the fiber orientation disappears if the fibers’ bending modulus is too high, showing that in this model, fiber orientation is sensed through mechanical interactions with the fibers. A model that links a fibrous network with breakable cross-links to a circular radial cell suggests that fiber accumulation can enhance cell–ECM adhesion by increasing the number of available binding sites for cellular adhesion (Cao et al., 2017). Altogether, these computational models have studied the potential effect of cell contractility on the ECM, but they did not include the reciprocal effects of the ECM on the cell (ii).

A number of models have considered only (ii), the effect of the ECM on cell behavior. For example, Vargas et al. (2020) showed how different cell migration modes can emerge based on adhesion maturation and stress fiber strength using a 3D finite element model of a moving cell on a non-fibrous, uniformly structured ECM. A different finite element model of cell migration showed how cell deformation and ECM porosity are of primary importance in amoeboid cell migration (Campbell and Bagchi, 2021).

Models combining (i) and (ii), thus closing the loop to full mechanical ECM reciprocity, include those by van Oers et al. (2014), Rens and Merks (2017), and Rens and Merks (2020). In these models, cell shape is modeled using the cellular Potts model (CPM) and coupled to a finite element (FEM) simulation of the ECM to form a hybrid CPM. Early CPM–ECM couplings assumed that cellular protrusions are stabilized on highly stressed substrates (van Oers et al., 2014), showing how mechanical cell–cell communication can play a role in angiogenesis. Subsequently, this coupling was extended by including a comprehensive model of mechanosensitive adhesion between the cell and the ECM, leading to emergent cell spreading, spontaneous cell elongation, and durotaxis (Rens and Merks, 2020). Although these models consider full mechanical reciprocity, their ECM is homogeneous, i.e., there are no fibers. One of the first models of mechanical cell–ECM reciprocity featuring a fibrous ECM was used to explain how bands form between two contractile cells in a fibrous ECM and how the two cells elongate toward each other by the remodeled matrix (see Reinhardt et al., 2013, reviewed in Crossley et al., 2024). Another sophisticated model of cell–ECM reciprocity is that of Kim M. C et al. (2018), where a triangulated dynamic cell is coupled to a fibrous ECM using an FEM simulation. They studied how cells can sense local stiffness in the fiber network by considering filopodia–fiber binding. In this study, we build upon our previously introduced hybrid CPM and molecular dynamics (MD) model (Tsingos et al., 2023). This model approximated the ECM by representing fibers using a beads-and-spring model, where the fibers were linked using cross-linkers. In this work, we modeled how the cell’s contractions form the ECM and how these deformations propagate far into the network. Furthermore, the cells’ contractile forces are counteracted by the ECM, leading to less contraction in a highly cross-linked, stiff ECM and high cellular contraction in a soft ECM. In this model, the cellular adhesions were static, and new adhesions could not be formed with the ECM.

To study the alignment of cells in anisotropic networks, we extend our previous hybrid CPM and molecular dynamics model (Tsingos et al., 2023) with dynamic adhesions. The choice of how to couple cellular morphology and ECM dynamics is delicate as it encodes the biological hypothesis of how cells sense and react with the ECM. In this work, we adopt the coupling between cell and ECM proposed by Rens and Merks (2020) and apply it to a hybrid CPM with discrete fibrous ECM (Tsingos et al., 2023). The coupling is made by assuming that the cell exerts cytoskeletal contraction forces through integrin-based adhesions that behave according to the two-spring model (Schwarz et al., 2006; Doyle et al., 2022). In essence, the two-spring model views adhesion as a mediator between the contractile forces of the cell and the restoring forces of the ECM. The tension on the adhesion builds up slowly on the soft ECM and quickly on the stiff ECM as the cell applies its contractile forces. Additionally, we assume that adhesions strengthen as tension increases. Adhesion strength is quantified by the number of integrin proteins bound to the adhesion. These assumptions, when combined with an isotropic material in a hybrid CPM, are sufficient to produce phenomena such as cell spreading, spontaneous elongation, and durotaxis (Rens and Merks, 2020). We implement this two-spring adhesion model in the hybrid CPM with a discrete fibrous ECM (Tsingos et al., 2023) and use the new model to investigate the reciprocity between fiber orientation and cell morphology. Specifically, with this new fibrous ECM model, we show how cell elongation on oriented gels can be considered a special case of stiffness-dependent cell spreading as fibers are easier to bend than to stretch. Furthermore, we study how cell protrusions can reorient fibers, thereby increasing tension on adhesions and stabilizing the protrusions.

2 Methods2.1 Modeling approach

We have introduced dynamic descriptions of mechanosensitive focal adhesions (FAs) into a hybrid CPM and MD model (Tsingos et al., 2023). The CPM part dynamically describes cell shape changes, and the MD part simulates a cross-linked network of ECM fibers and its dynamical response to cellular forces. In our previous work, the CPM was connected to the MD model through static adhesion particles. In the present model, the buildup and breakdown of FAs are modeled dynamically using an ordinary differential equation model that describes FAs as clusters of integrins, with the breakdown rate assumed to be dependent on the mechanical tension within the FAs. This ordinary differential equation (ODE) model for FAs and their constituent integrins was adapted from the work by Novikova and Storm (2013), as shown in one of our previous models featuring a continuum description of the ECM (Rens and Merks, 2020). Figure 1 provides an overview of the key elements of the model.

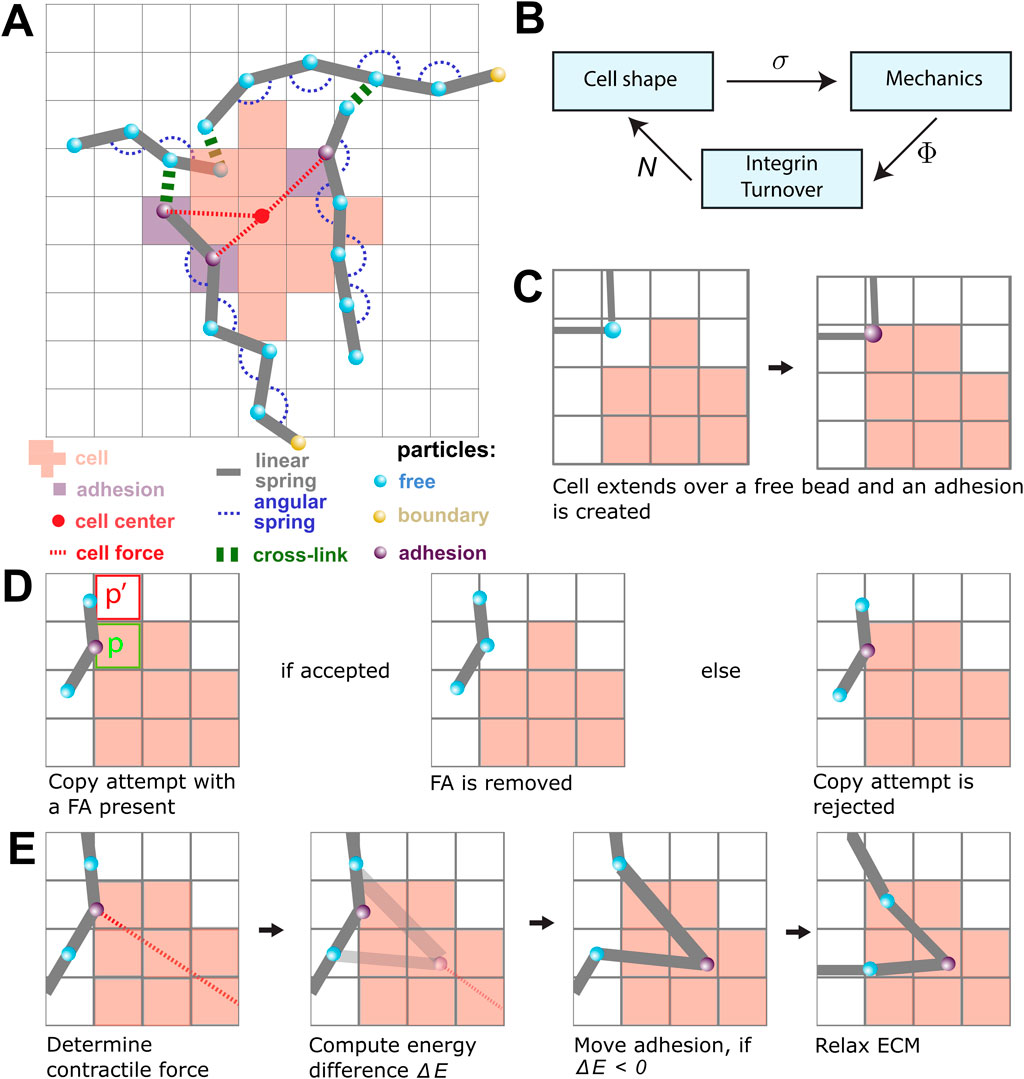
Figure 1. An overview of the model components and the model rules. (A) A schematic overview of the components in the model. The lattice-bound cellular Potts cell (red squares) is attached to the beads (cyan) and springs (gray) of the ECM through the focal adhesions (FAs; purple). The contractile force (dashed red) is visualized between FAs and the center of mass of the cell (red point). FAs connect the cell to the strands of the ECM. The strands are cross-linked (green), and particles outside the simulation domain are fixed (yellow). (B) The submodels of the model are coupled as shown in this figure. The CPM is responsible for the cell shape and sends the lattice state σ to the mechanical part of the model. The mechanical part computes the tensions Φ in the FAs and gives this to the FA part of the model. The tensions are used to calculate the number of bound integrins N(i) for each FA i. These numbers are then used in the CPM to update the new cell shape. (C) A scheme showing the creation of a new FA. When a cell extends over a free bead, it becomes an adhesion bead. (D) Scheme showing a retraction copy-attempt when an FA is present. The FA is removed if the copy-attempt is accepted (left). The presence of the FA increases the likelihood of rejecting the copy-attempt (right). (E) An FA is pulled toward the center of the cell in a process resembling a CPM copy-attempt: first, the energy change between the original position of the FA and the new FA is determined by only considering springs that are directly attached to the FA. The FA is moved if the energy difference is negative. Finally, the complete ECM is relaxed by running the molecular dynamics simulation.

The models are coupled using an operator-splitting approach. The three submodels are sequentially iterated to a steady state, where the output state of one submodel is used as the input state for the next submodel (Figure 1B). The simulations were run until a quasi-steady state was reached, i.e., until no large further changes were observed. In the remainder of this section, we will describe each of the three submodels and the coupling strategies.

2.2 Cellular Potts model

To describe cell shape changes, we employ the cellular Potts model (Graner and Glazier, 1992; Hirashima et al., 2017). The CPM is a lattice-based model in which cell shape is defined as a collection of connected lattice sites. We implemented a CPM on a square grid Λ⊆Z2 of 200×200 lattice sites. Each lattice site x⃗∈Λ is assigned a spin σ(x⃗)∈Z≥0, which defines a spin field σ:Λ→Z≥0. The collection of connected lattice sites that have the same positive spin n defines the shape of the cell n. As shown in Figure 1A, the red lattice sites indicate the shape of a single cell. The set of lattice sites with spin 0 is not occupied by a cell.

The CPM evolves through a sequence of random extensions and retractions, whose probability is given by a balance of contractile and extensile forces and forces due to adhesion with the ECM. These are given by a Hamiltonian energy function.

Hσ=λA2+∑x⃗∈Λ∑x⃗′∈NBx⃗Jσx⃗σx⃗′1σx⃗≠σx⃗′−λcAA+Ah,(1)

where A=|| is the area of the cell, NB(x⃗) is the set of lattice sites in the neighborhood of x⃗, and λ, J, λc, and Ah are parameters. The first part of Equation 1 describes the contractility of the cell with magnitude λ. The second term penalizes, with strength J, interfaces between the cell and the medium, effectively creating a line tension along the cell’s perimeter. The final term describes the formation of non-integrin-based adhesions with the substrate, which bind with a strength parameter λc and a saturation parameter Ah.

The Hamiltonian is minimized through Metropolis dynamics, as previously described by Graner and Glazier (1992), thus dynamically updating the cell’s shape. In brief, we iteratively select a random lattice site x⃗ and a random adjacent lattice site x⃗′. We then calculate the energy difference ΔH that would result due to the update and accept the copy attempt with probability P(ΔH)=1 if ΔH≥0, and P(ΔH)=exp(−ΔH/T) for ΔH>0, where T is a cell motility parameter.

The acceptance probability of a copy attempt is determined by the energy change:

ΔH=Hσx⃗′−Hσx⃗+ΔHFA,(2)

where ΔHFA is an additional penalty for breaking integrin bonds that the cell might have with the ECM at that location.

The term ΔHFA in Equation 2 is non-zero only if the copy attempt corresponds to a retraction from a site x⃗∈Λ that contains an FA, and in this case,

ΔHFA=λFA∑N∈Nx⃗N−N0∑N∈Nx⃗N−N0+Nh,

where N(x⃗) represents the number of integrins in the FAs situated at x⃗, λFA represents a scaling parameter, N0 represents the initial size of an FA, and Nh represents a saturation parameter. If a copy attempt is accepted that leaves an FA outside of the cell, the FA is removed, as shown in Figure 1D. If a copy attempt is accepted that extends over a free bead of the ECM, then a new FA is created, as shown in Figure 1C.

2.3 Extracellular matrix model

The ECM is described as a set of fibers connected through cross-linkers, forming a fiber network that is superimposed on the CPM lattice (Figure 1A). A fiber is built out of nbeads beads, which are linked together with springs of stiffness Kpolymer and rest length rpolymer. Fibers are illustrated in Figure 1A, where the blue beads are connected by gray springs to form different fibers. Next to springs linking beads into fibers of contour length rpolymer⋅(nbeads−1), consecutive triplets of beads in a fiber are connected with a harmonic potential with bending rigidity Kbend. This angular constraint ensures that unforced fibers remain straight and are illustrated with dashed blue curves in Figure 1A. To create a network, cross-linkers are added to the fibers (the green dashed lines in Figure 1A). Cross-links are defined as springs with a small rest length and stiffness equal to Kcross=Kpolymer and link different fibers together to form a connected network.

To create a fiber network, we followed the method introduced by Tsingos et al. (2023) with small modifications for creating networks of aligned fibers. In brief, we distributed Nstrands randomly and uniformly in space, selecting fiber orientations from the von Mises distribution to control the degree of fiber alignment. Fibers were created as follows: the position of the middle bead b⃗k∈Λ with k≔floor(nbeads/2) of a strand was selected at random from a uniform distribution, and a random angle θ∈[0,2π) was selected from the von Mises distribution with μ∈0,2π and κ∈0,∞. Then, the remaining positions x⃗i making up the beads were defined via

b⃗i=b⃗k+i−krpolymerv⃗,for i∈0,…,nbeads−1,

where v=(cos⁡θ,sin⁡θ) is a unit vector with angle θ. Constructing the fiber positions in this way ensures that the middle of each fiber is within the simulation domain, while only the endpoints might extend beyond the simulation domain. After the fibers have been introduced, the network is cross-linked as described in the previous work by Tsingos et al. (2023).

The springs connecting pairs of beads and the bending rigidity connecting triples of beads impose forces on the ECM and make the fiber network dynamic. The positions of the beads b⃗1(t),…,b⃗n(t)∈R2 are governed by the overdamped Langevin equation of motion

γdragddtb⃗i=F⃗i+W⃗i,(3)

where γdrag is a drag coefficient, Fi is the force on the ith particle, and W⃗i is a random force satisfying ⟨W⃗i⟩=0 and ⟨W⃗i2⟩=2γdragTECM/Δt with TECM representing a parameter for degree of noise in the system and Δt representing the size of a timestep. Equation 3 was integrated to a steady state, with fixed Δt during the simulation using the HOOMD-blue molecular dynamics library (Anderson et al., 2020).

The energy of a single spring with a rest length r0 and spring constant k, connecting a pair of beads (i,j), is determined by the potential:

Uij=k2Δrij2,whereΔrij=r0−‖bi−bj‖2,

where ‖(x,y)‖2=x2+y2 is the Euclidean norm. Similarly, the harmonic potential between a triple of beads (i,j,k) is defined as

Uijk=Kbend2Δθ,whereΔθijk=shortest angle between b⃗i,b⃗j,b⃗k.

where Kbend is the bending rigidity. Some beads are fixed in space and are excluded from Equation 3. These beads are at the boundary of the system, effectively clamping the ECM at the sides of the integration domain.

2.4 Focal adhesions

FAs, schematically shown as purple beads in Figure 1A, are modeled as clusters of catch-slip bonds (Novikova and Storm, 2013; Rens and Merks, 2020; Schwarz et al., 2006). Each cluster is assumed to be in constant flux as integrins are added and removed from the cluster. The integrin addition rate is independent, whereas the removal rate is suppressed by mechanical tension due to the contractile force of the cell and the restoring force from the ECM. The number of integrins N in a single focal adhesion is the size of that FA and changes when under tension Φ following the equation:

dNdt=γNtot−N−d0df∗ΦNN,(4)

where γ is the binding rate of integrins, Ntot is the maximum number of integrins in a single FA (Changede and Sheetz, 2017), d0 is the base detachment rate, f∗ is the force scale, and d(φ) is a function of the tension per integrin that encodes the response of mechanical tension to the unbinding rate of a single integrin. We use a model for a catch-slip integrin that takes the following form:

where ϕs and ϕc describe the slip and catch regime of an integrin, respectively (Novikova and Storm, 2013; Rens and Merks, 2020).

The tension Φ on the FAs is due to the force balance of the contractile cellular force and the resultant force from the ECM. To calculate the contractile force, we assume that the cell’s cytoskeleton applies a force proportional to the distance from the cell center (Lemmon and Romer, 2010), effectively modeling the cytoskeleton as a spring connecting each FA to the cell’s center, as sketched in Figure 1A with the dashed red lines connecting purple adhesion particles to the cell center. The energy that the cytoskeleton exerts is then assumed to be Ecyto=∑x⃗Kcyto2(x⃗−x⃗center)2, where x⃗ is the position of an FA, x⃗center is the center of the cell to which the FA belongs, and Kcyto is a spring constant encoding the isotropic cell force. Similarly, the energy of parts of the ECM that are directly linked to the FA is defined as Eecm. An FA is then displaced using an algorithm that is similar to the CPM algorithm: We attempt to move an FA one lattice site toward the cell center, and this movement is accepted if it is energetically favorable. Otherwise, the movement is rejected. Specifically, we first compute the total energy E=Ecyto+Eecm. Then, the energy E′ is computed if the FA was moved one lattice site toward the center of the cell. If the difference E′−E is negative, the FA is moved to the new position; otherwise, it is kept in place. This means that FAs are moved independently from each other and can lead to multiple FAs, occupying the same lattice site. Furthermore, the energies E are independent of Equation 1, which describes the energy of the cell.

2.5 Parameter values

Table 1 lists the parameter values used for the CPM and MD models. They are dimensionless and require scaling to fit to measurable quantities. We follow the previous work by Tsingos et al. (2023) for this scaling, and we briefly summarize the main points in this section. A single lattice site of the CPM is set equal to 0.25μm×0.25μm, and 104 model timesteps is roughly 8 h. The CPM parameters λ, J, λc, T, and Ah are calibrated to show generic cell area and activity in the absence of the ECM, and the FA parameters γ, d0, and f∗ were estimated such that the final FA size distribution was wide enough to differentiate between softer and stiffer parts of the ECM. As in our previous work, we fit the force units of the model to match up on the widely varying tensile modulus Y of collagen. We set Y=106Pa, which yields a spring constant of 3.1⋅10−2Nm−1. As described by Tsingos et al. (2023), tensile modulus is converted into the spring constant by approximating a single collagen fiber as a cylindrical rod of diameter 0.125μm and applying the formula K=YA/L, with A representing the cross-sectional area and L representing the length of a collagen segment. This choice results in a contraction force of 3.1⋅10−4Nm−1, leading to typical traction forces ranging from 8nN to 15nN on a single FA, with a total range of 10−8 to 10−10N. These values are slightly lower than those reported by Tsingos et al. (2023) but fall in the correct order of magnitude for cell traction forces (Wakatsuki et al., 2000; Labernadie and Trepat, 2018). Although most parameters in this model were estimated to produce reasonable behavior, the predicted dynamics and interactions provide insights into the role of mechanical reciprocity in cell biology.

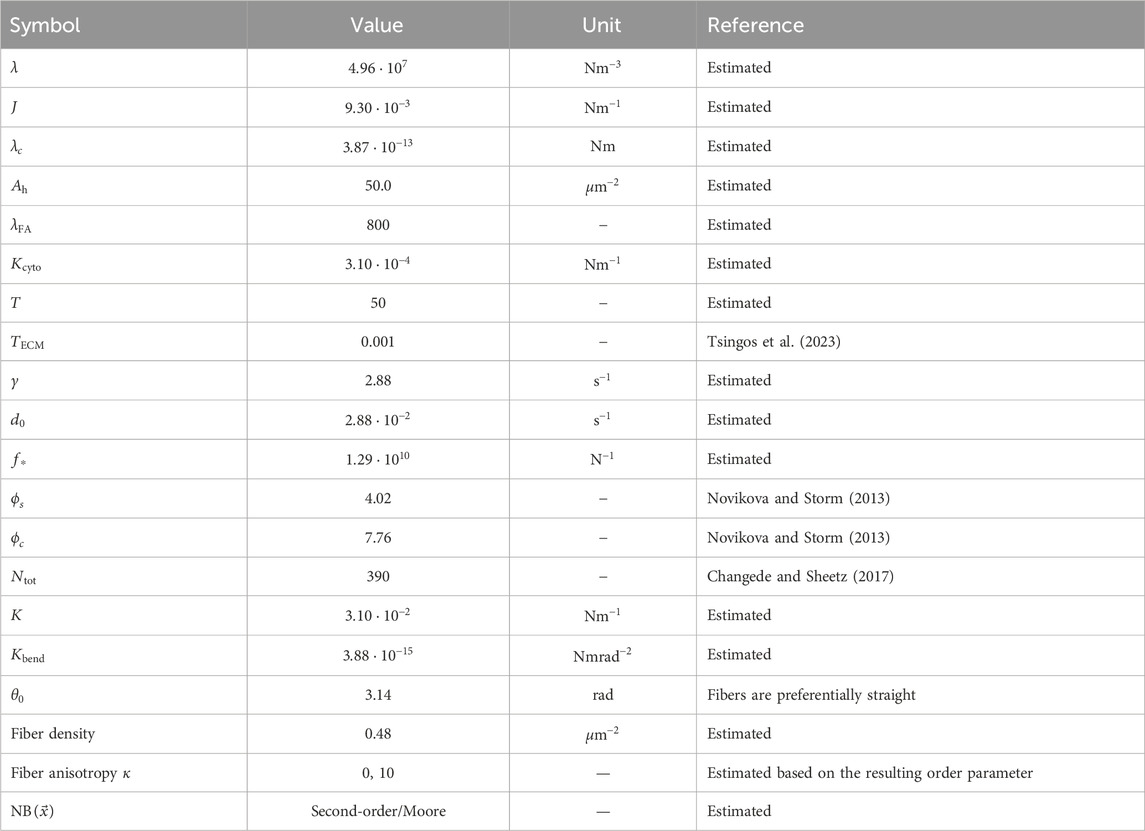
Table 1. Parameter values used in the simulations unless otherwise specified. The parameter values reported here are the scaled values, which is why they may appear as non-rounded numbers despite being chosen values.

2.6 Statistical significance

The error bars shown in Figures 2–4 denote the mean ±1 standard deviation. Statistical significance: we computed a p-value using the Welch’s test, which we reported with the following symbols: (ns) p≥0.05, (*) p<0.05, (**) p<0.01, (***) p<0.001, and (****) p<0.0001.

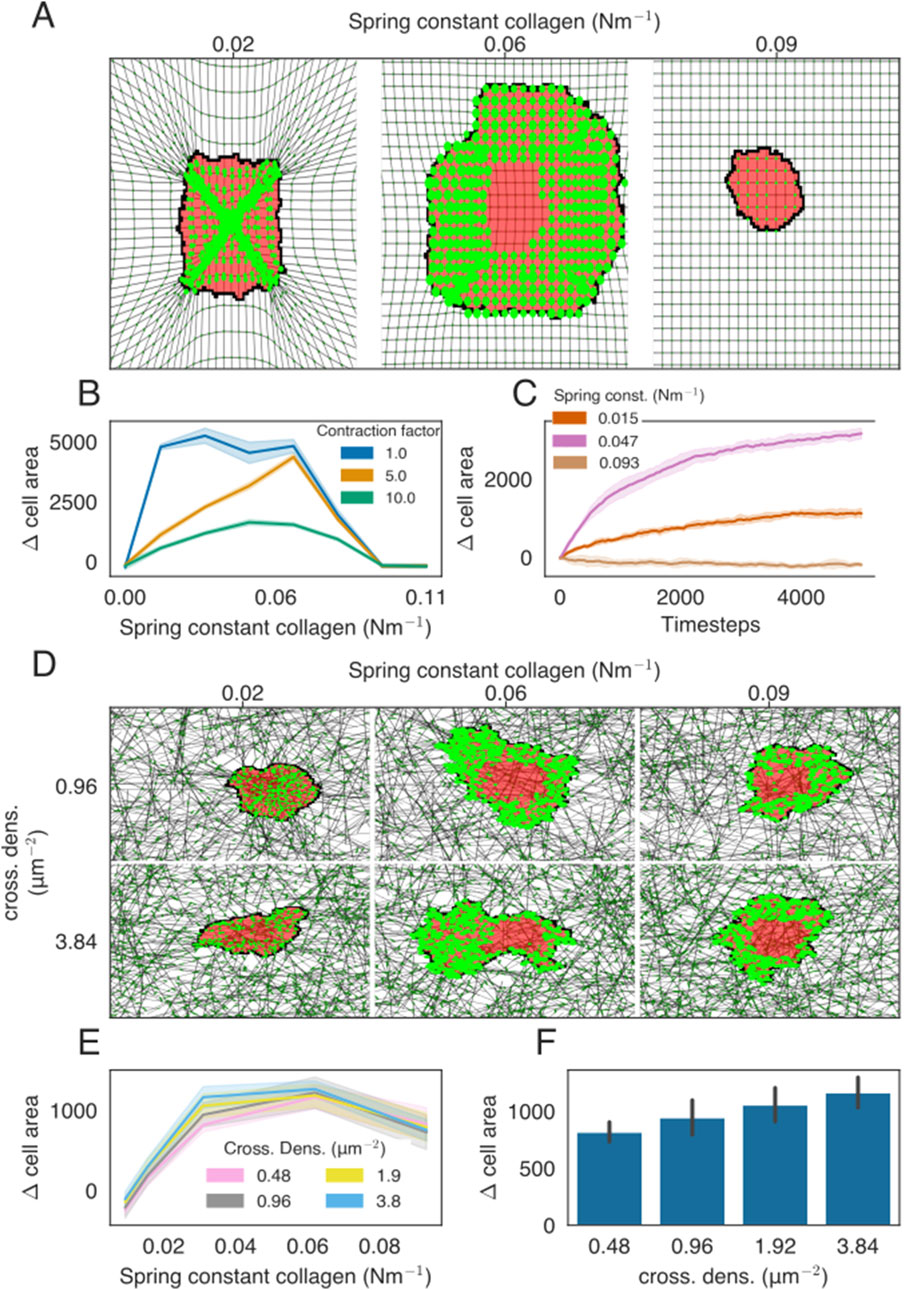
Figure 2. Cell spreading on isotropic ECMs with regular or network structures. (A) Example of cell spreading on an isotropic ECM for three different spring stiffness values. The cell is colored in red, FAs are presented as bright-green discs, ECM strands are in gray, and ECM crosslinks are shown in dark green. The radius of the bright-green discs is proportional to the size of the FAs. All FAs are assigned to only a single lattice site, even if the visualization may suggest otherwise. (B) Difference in the cell area from the starting size for the ECM of different stiffness. Colors indicate the factor by which the contraction force of the cell is multiplied. (C) Time-evolution of the cell area as a function of ECM spring stiffness. (D) Simulation snapshots of cell spreading on the isotropic ECM for a range of spring constants and cross-link densities. (E) Difference in the cell area from the starting size, at t=0, for ECM of different stiffnesses. Colors indicate the cross-link density. (F) Bar graph showing the final cell size as a function of collagen density, with stiffness parameter K=0.031Nm−1.

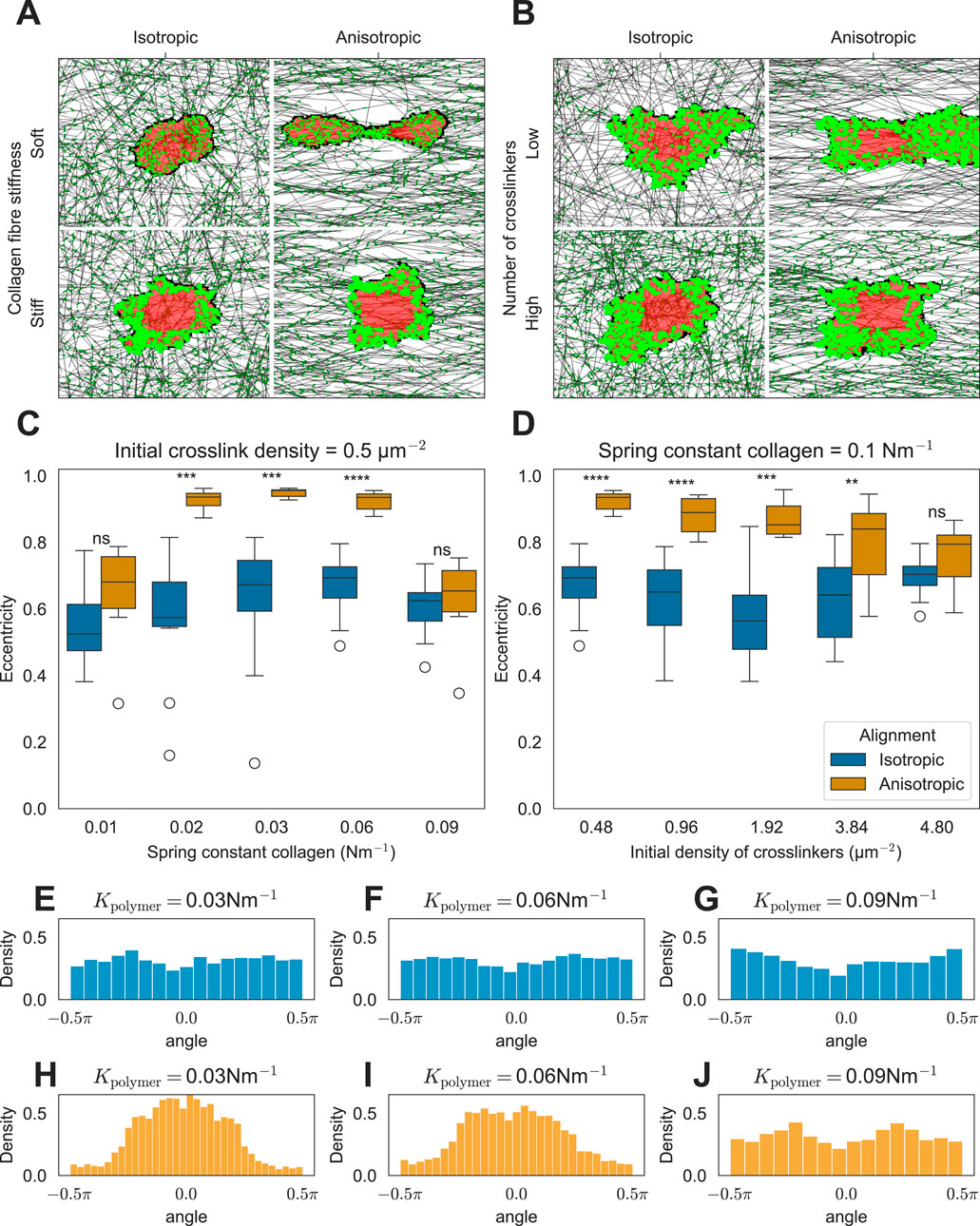
Figure 3. Effect of ECM anisotropy on the cell shape. (A) Snapshots of simulations showing the effect of matrix anisotropy on the cell shape as a function of collagen stiffness (K = 0.016Nm−1 (soft) and K=0.093Nm−1 (stiff)). (B) Snapshots of simulations showing the effect of matrix anisotropy on the cell shape as a function of cross-linker density ([Ncross]=0.48μm−2 (low) and [Ncross]=4.8μm−2 (high)). (C) Distribution of cell eccentricities as a function of collagen stiffness (K). Distribution of cell eccentricities as a function of cross-linker density (D). (E–J) Distributions of FA angles relative to the horizontal axis passing through the cell’s center of mass are shown for isotropic ECM conditions (E–G) and anisotropic ECM conditions (H–J).