Dopaminergic neurons (DAs) are specialized neurons tasked with dopamine secretion, which is crucial in regulation of muscle movement, and cognitive function [1, 2]. DAs are primarily located in specific regions of the brain, including the substantia nigra (SN) and the ventral tegmental area [1, 3]. These neurons can respond to extracellular excitation by activation of internal calcium signaling that lead to dopamine secretion [4–6]. A common feature of DAs (typically those projecting to the dorsal striatum and lateral shell of the nucleus accumbens) is their intrinsic 'pacemaker' activity, characterized by autonomous action potential (AP) and calcium oscillations even in the absence of external perturbations [7, 8]. These oscillations were shown to be crucial in regulating basal dopamine levels and exhibit robust frequency under various conditions and in different in-vitro and in-vivo models [9–11].
Dopamine secretion occurs when intracellular calcium ion (henceforth denoted by Ca2+) concentrations increase above a certain threshold [12–14]. The dynamics of Ca2+ are coupled to the dynamics of other ions in the cytoplasm, primarily sodium (Na+) and potassium (K+) [15, 16]. All the ionic fluxes into & out of the cell are coupled via the plasma membrane potential (MP), which modulates the activity of numerous Ca2+, Na+ and K+ channels and pumps [17]. Typically, an inward flux of Na+ is triggered due to external stimulation of voltage activated Na+ channels. The Na+ flux depolarizes the membrane, leading to an action-potential (AP) event, triggering the opening of Ca2+ channels. This creates an inward flux of Ca2+ that increases intracellular Ca2+ concentration. In response to depolarization, an inward flux of K+ ions hyperpolarize the membrane and leads to a halt in Na+ entry. The baseline ionic concentrations (and membrane voltage) are then restored through the pumping of K+, Na+ & Ca2+ against their electrochemical potential (primarily 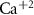 and Na+/K+ pumps 2) in an Adenosine triphosphate (ATP) dependent manner. This tight regulation of intracellular Ca2+ is crucial to the physiological status of cells [18–20]. Thus, Na+/K+ coupled Ca2+ signaling is an energy intensive process, which constitutes up to ∼20%–50% of the cellular energy demand [21–24].
and Na+/K+ pumps 2) in an Adenosine triphosphate (ATP) dependent manner. This tight regulation of intracellular Ca2+ is crucial to the physiological status of cells [18–20]. Thus, Na+/K+ coupled Ca2+ signaling is an energy intensive process, which constitutes up to ∼20%–50% of the cellular energy demand [21–24].
Despite the high energy demands, an important characteristic of DA neurons is that they display spontaneous AP firing and Ca2+ oscillations in-vitro and in-vivo, even in the absence of external stimulation. While most DAs show regular oscillations, perturbed DA neurons display rich dynamics of Ca2+ and AP oscillations, from quiescence, to tonic (regular), to 'bursting' (a combination of several frequencies, where the AP undergoes a period of rapid oscillations followed by quiescence) [25–27]. It is hypothesized that these spontaneous Ca2+ oscillations are crucial for the functionality of DAs, determining basal and on-demand secretion of dopamine [12, 28]. However, prolonged elevated Ca2+ concentrations may impair lysosomal motility, increases generation of reactive oxidative species, and impair mitochondrial ATP synthesis, all reducing cell viability [18–20]. Thus, regulation of Ca2+ balances the requirements of cellular function, with the constraints of cell survival. Mechanisms that rely on oscillatory calcium signals have been proposed to do just that [29, 30]. This may explain why DAs are susceptible to damage and degeneration, a common feature of several neurological pathologies including Parkinson's disease (PD) [2, 31].
Various kinetic models have been previously proposed to study Ca2+ oscillations and signaling in (DA) neurons [32–38]. Several, single-compartment models that couple the Hodgkin and Huxley model for AP generation [17] to Ca2+ dynamics have successfully captured many DA experimental observations (tonic firing, Ca2+ oscillations, response to external stimuli, pharmacological intervention etc. [32, 33, 36]). These models implicate various ion channels in facilitating Ca oscillations [39]. Other models extend the treatment to a multi-compartment system, to account for spatial organization and coupling between different regions of the cell (dendrites, soma & axons), which more realistically captures the complexities of neuronal morphology [34, 35]. While some models do take into account Na+ and K+ dynamics [38], most of these models assume constant cytoplasmic Na+ and K+ concentrations, justified by a narrow range of average concentrations observed in simulations and experiments, and the small amplitudes of Na+ & K+ oscillations when compared to these measured averages (∼0.1% change) [38]. This implies that the transient change in Na+ & K+ (∼nM scale) is negligible compared to their average concentration (>10 mM). However, fixing intracellular ionic concentrations in simulations prevents the system from evolving naturally towards its homeostatic conditions.
In this paper, we present a kinetics one-compartment, conductance-based model for isolated neurons that follows the dynamics of the MP, Ca2+, ADP, as well as Na+ and K+ over time. Our focus is not on the specific channels and pumps that facilitate Ca2+ exchange, but on the general interaction between Ca2+ and AP dynamics, and the impact on functionality (dopamine secretion). We choose a hybrid approach where we adopt most of the kinetics model described in [33], infused with several other kinetic expressions of interest from [32, 36, 40]. Crucially, kinetic expressions for the dynamics of Na+ and K+ are also included. The model captures the essential features of DA neurons' dynamics, including spontaneous firing and Ca2+ oscillation. Our results illustrated how relaxing the Na+ and K+ fixed-values approximation results in a higher tendency for spontaneous tonic oscillations, as well as a more robust oscillation frequency. We further discuss the impact of the transition from tonic to 'bursting' oscillations on the coupled Ca2+ oscillations, which encode to a broad spectrum of signals while maintaining relatively constant average calcium levels and metabolic loads.
2.1. Model descriptionBased on the works of [32, 33, 36, 40] we construct a one-compartment, conductive-based kinetic model that describes the dynamics of the MP (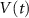 ), as well as intracellular Ca2+ (
), as well as intracellular Ca2+ (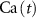 ), Na+ (
), Na+ (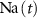 ), K+ (
), K+ (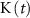 ), and ADP (
), and ADP (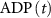 ) concentrations. We consider all external ion concentrations (
) concentrations. We consider all external ion concentrations (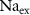 ,
, 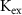 ,
, 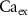 ) as control parameters and not variables. Ionic currents are passively conducted (according to their electrochemical potential) via several types of voltage-activated channels for Na+ (Na-VGC), K+ (K-VGC, S-K, K-ATP) and Ca2+ (L-type, T-type), and their corresponding leak channels (Na-Leak, K-Leak, and Ca-Leak). Note that the activity of the S-K and K-ATP channels also displays threshold activation in response to high Ca2+ and ADP concentrations respectively, which serve as regulators of both concentrations. These currents are counterbalanced by the activity of two pumps; the sodium-potassium pump (Na+/K+ ATPase) and a Ca pump (Ca2+ATPase), both catalyzing ATP to actively move ions against their electrochemical gradients. ATP is constantly synthesized by the cell, to facilitate this active ion transport across the membrane.
) as control parameters and not variables. Ionic currents are passively conducted (according to their electrochemical potential) via several types of voltage-activated channels for Na+ (Na-VGC), K+ (K-VGC, S-K, K-ATP) and Ca2+ (L-type, T-type), and their corresponding leak channels (Na-Leak, K-Leak, and Ca-Leak). Note that the activity of the S-K and K-ATP channels also displays threshold activation in response to high Ca2+ and ADP concentrations respectively, which serve as regulators of both concentrations. These currents are counterbalanced by the activity of two pumps; the sodium-potassium pump (Na+/K+ ATPase) and a Ca pump (Ca2+ATPase), both catalyzing ATP to actively move ions against their electrochemical gradients. ATP is constantly synthesized by the cell, to facilitate this active ion transport across the membrane.
Like the original model of [33], our model inherits the characteristic compartment size 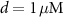 , which may be interpreted as the characteristic width of a dendrite, or a small volume in the vicinity of the somatic membrane which is well mixed in the relevant timescales of the model (1 ms—1 sec). Beyond such length scales, diffusion becomes a limiting process, and the model may need revision. Our focus here is on spontaneous oscillations & the electrical properties of isolated neurons, in the absence of external perturbations. Thus, we omit the expressions for NMDA (external stimulation) channels, which been shown to coordinate synaptic stimulation, and regulate firing pattens in DA neurons [41]. A schematic illustration of the various fluxes is presented in figure 1(A), with an analogous circuit diagram presented in figure 1(B). The kinetic expressions for the voltage-activated and leak channels currents are adopted from [33]. The kinetic expressions for the Na+/K+ and Ca pumps are adopted from [32] and were constrained to 0 at low ATP levels by adopting Michaelis–Menten kinetic scheme observed in [40]. The model parameters were adjusted to better fit physiological conditions and observed tonic frequencies, based on the works of [36, 40, 42]. The changes, and their reasoning are listed in section S1 of the SI.
, which may be interpreted as the characteristic width of a dendrite, or a small volume in the vicinity of the somatic membrane which is well mixed in the relevant timescales of the model (1 ms—1 sec). Beyond such length scales, diffusion becomes a limiting process, and the model may need revision. Our focus here is on spontaneous oscillations & the electrical properties of isolated neurons, in the absence of external perturbations. Thus, we omit the expressions for NMDA (external stimulation) channels, which been shown to coordinate synaptic stimulation, and regulate firing pattens in DA neurons [41]. A schematic illustration of the various fluxes is presented in figure 1(A), with an analogous circuit diagram presented in figure 1(B). The kinetic expressions for the voltage-activated and leak channels currents are adopted from [33]. The kinetic expressions for the Na+/K+ and Ca pumps are adopted from [32] and were constrained to 0 at low ATP levels by adopting Michaelis–Menten kinetic scheme observed in [40]. The model parameters were adjusted to better fit physiological conditions and observed tonic frequencies, based on the works of [36, 40, 42]. The changes, and their reasoning are listed in section S1 of the SI.
Figure 1. Model description. (A) A schematic illustration of model fluxes through K (green), Na (blue) & Ca (yellow) voltage-gated channels (VGCs) with chemical activation (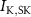 ,
, 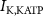 ) and without (
) and without (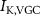 ,
, 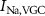 ,
, 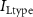 ,
, 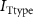 ), leak channels (
), leak channels (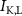 ,
, 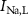 ,
, 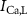 ), Ca and Na/K pumps (
), Ca and Na/K pumps (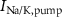 ,
, 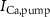 ), and the ATP consumption and synthesis (mitochondria). (B) An analogous circuit diagram of the model.
), and the ATP consumption and synthesis (mitochondria). (B) An analogous circuit diagram of the model.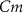 represents the membrane capacitance and
represents the membrane capacitance and 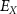 represent the Nernst potentials for
represent the Nernst potentials for  . Components are in the same order as panel (A). (www.circuit-diagram.org/editor/).
. Components are in the same order as panel (A). (www.circuit-diagram.org/editor/).
Download figure:
Standard image High-resolution imageThe dynamics of the cellular MP 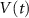 are described by the following implicit equation:
are described by the following implicit equation:
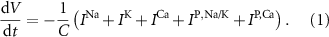
With 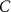 the capacitance of the membrane,
the capacitance of the membrane, 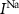 ,
, 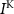 and
and 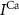 the passive currents through various ion channels corresponding to Na+, K+ and Ca2+ respectively, and
the passive currents through various ion channels corresponding to Na+, K+ and Ca2+ respectively, and 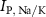 and
and 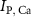 the ATP dependent currents through the Na+/K+ and Ca2+ pumps (respectively). Each ionic variable is subjected to a kinetic equation that balances the stoichiometric ratio of ion exchange:
the ATP dependent currents through the Na+/K+ and Ca2+ pumps (respectively). Each ionic variable is subjected to a kinetic equation that balances the stoichiometric ratio of ion exchange:
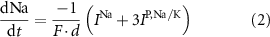
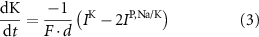
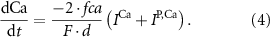
With 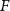 noting Faraday's constant,
noting Faraday's constant, 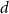 the compartment width (i.e.—axonal radius), and
the compartment width (i.e.—axonal radius), and  the coarse-grained fraction of free Ca2+ in the cytosol (i.e.—the buffering capacity due to various Ca2+ binding proteins). The kinetics of ADP turnover are described by:
the coarse-grained fraction of free Ca2+ in the cytosol (i.e.—the buffering capacity due to various Ca2+ binding proteins). The kinetics of ADP turnover are described by:
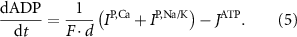
With 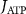 the ADP dependent production rate of ATP. Note that we do not consider ATP consumed by other cellular processes (i.e.—background consumption) to solely focus on the role of ATP consumption by the active transport of ions. In a sense, equation (5) stands for the turnover dynamics of the fraction of ATP allocated to maintaining ion homeostasis. ADP turnover is supplemented by the assumption of a conserved adenosine backbone concentration, i.e.—
the ADP dependent production rate of ATP. Note that we do not consider ATP consumed by other cellular processes (i.e.—background consumption) to solely focus on the role of ATP consumption by the active transport of ions. In a sense, equation (5) stands for the turnover dynamics of the fraction of ATP allocated to maintaining ion homeostasis. ADP turnover is supplemented by the assumption of a conserved adenosine backbone concentration, i.e.—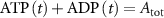 , with
, with 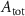 the total adenosine concentration. The conductance of the voltage activated channels is depicted via a Hodgkin–Huxley formalism [17, 32, 33], describing the voltage sensitivity through the dynamics of six additional gating variables: K-VGC activation (
the total adenosine concentration. The conductance of the voltage activated channels is depicted via a Hodgkin–Huxley formalism [17, 32, 33], describing the voltage sensitivity through the dynamics of six additional gating variables: K-VGC activation (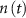 ), Na-VGC activation (
), Na-VGC activation (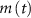 ) and inactivation (
) and inactivation (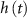 ), L-type activation (
), L-type activation ( ) and T-type activation (
) and T-type activation (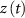 ) and inactivation (
) and inactivation ( ). The gating is described via a Hodgkin-Huxley like dynamics, with the general equation:
). The gating is described via a Hodgkin-Huxley like dynamics, with the general equation:
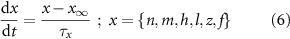
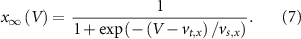
With 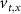 ,
, 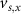 and
and 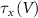 the threshold, steepness, and voltage dependent response time respectively for the activation (inactivation) function of each of the gating variables
the threshold, steepness, and voltage dependent response time respectively for the activation (inactivation) function of each of the gating variables 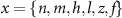 . The values of the
. The values of the 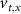 ,
, 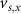 , and the expression for
, and the expression for 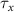 are taken from [32, 33] (see table S1 in the SI). An exception to this is the parameters associated with
are taken from [32, 33] (see table S1 in the SI). An exception to this is the parameters associated with 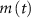 , which we modified to
, which we modified to 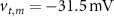 and
and  (within the range of accepted values [33, 36, 39]) to obtain spontaneous ∼1.8 Hz AP oscillations, as observed in DA neurons [7, 10, 15]. We further assume an instantaneous response to voltage changes by the
(within the range of accepted values [33, 36, 39]) to obtain spontaneous ∼1.8 Hz AP oscillations, as observed in DA neurons [7, 10, 15]. We further assume an instantaneous response to voltage changes by the 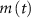 variable by approximating,
variable by approximating,  and thus
and thus 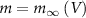 [32].
[32].
The explicit expressions for the current terms are given by the following set of equations:
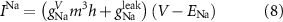
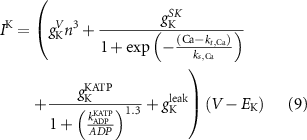
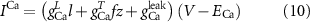
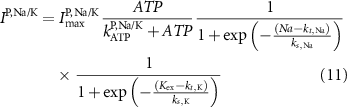
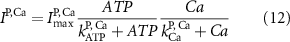
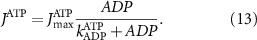
Here, the subscript 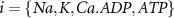 represents the specific variable associated with each parameter, and the superscript
represents the specific variable associated with each parameter, and the superscript  indicating the associated protein/process of (in order): VGC, passive leak, S-K channel, K-ATP channel, L-type Ca2+ channel, T-type Ca2+ channel, Sodium potassium pump, Ca pump and ATP production (see figure 1(A)).
indicating the associated protein/process of (in order): VGC, passive leak, S-K channel, K-ATP channel, L-type Ca2+ channel, T-type Ca2+ channel, Sodium potassium pump, Ca pump and ATP production (see figure 1(A)). 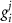 represent channel conductance,
represent channel conductance, 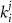 various Michaelis–Menten or Hill coefficients for threshold concentrations,
various Michaelis–Menten or Hill coefficients for threshold concentrations, 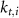 and
and  a sigmoidal threshold and 'steepness' concentrations, and
a sigmoidal threshold and 'steepness' concentrations, and 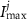 &
& 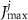 maximal currents and fluxes.
maximal currents and fluxes.  stands for the Nernst potential for the i'th ion, with
stands for the Nernst potential for the i'th ion, with  the valency,
the valency, 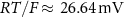 and
and 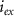 the extracellular concentration of the respective ion. Overall, our model includes a total of 10 ODEs, two algebraic equations, ten variables and thirty-one parameters (see table 1 for baseline values). The initial conditions for all simulations are given in table 2. For constant Na+ and K+ concentrations, we set in equations (2) and (3)
the extracellular concentration of the respective ion. Overall, our model includes a total of 10 ODEs, two algebraic equations, ten variables and thirty-one parameters (see table 1 for baseline values). The initial conditions for all simulations are given in table 2. For constant Na+ and K+ concentrations, we set in equations (2) and (3) 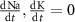 .
.
Table 1. Model parameters.
ParameterBaseline valueParameterBaseline valueParameterBaseline value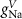 (*)
(*)
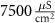 d
10−4
d
10−4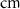
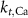 1.9*10−4
1.9*10−4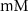

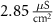 F
F
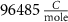
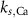 4*10−6
4*10−6
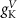 (*)
(*)
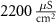

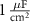
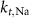 25
25 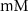
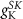 (*)
(*)
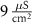
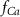 (*)0.02
(*)0.02
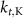 5.5
5.5 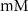
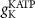 (*)
(*)
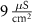
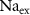 (*)127
(*)127 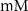
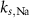 3
3 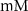

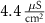
留言 (0)