Parallel measurements of the fluorescent signal of the calcium-sensitive dye Calcium Green-1 and the unspecific dye Texas Red together with the tube radius dynamics allow us to relate the contraction dynamics of the tube to the calcium concentration. Fluorescence in the green and red channels as well as the tube radius are measured along the one-dimensional representation, the skeleton, of the excised tube every 3 s. As the network evolves over time, we restrict the analysis to positions along the skeleton that are part of the skeleton for the entire experiment. Furthermore, we account for the time delay between the imaging in the two channels due to the switching of the respective filter cubes. Thus, the time series are interpolated and shifted with respect to each other by half a frame resulting in a symmetric relation of the signals avoiding inherent shifts. Finally, the ratio between the average intensities of the green and the red channel yields the cross-sectionally averaged concentration,

Even though the concentration is only known up to a constant prefactor, this ratio independent of variations in tube volume due to contractions is referred to as calcium concentration. Kymographs for four data sets of the tube radius and the calcium concentration are shown in figures S1–S4. To investigate the interplay of calcium and contractions, we calculate the phase-dependent calcium concentration. For that each time point is assigned to a contraction phase φ using a Hilbert transform (see (d) in S1–S4). The phase is calculated based on the band-passed radius time series with a band-pass set to be around the dominant frequency, which typically is around . A phase-dependent calcium signal is calculated by averaging over the calcium concentrations in the kymograph assigned to the same binned instantaneous phases.

Finally, the shift is determined as the phase shift between the main oscillation of the radius and the concentration approximated by a sinusoid, such that a shift of 0 indicates an anti-phasic relation and a positive shift indicates that the radius peaks before the calcium concentration reaches its minimum. Photo-bleaching of the fluorescent dyes is slow compared to the contraction time scale of the tubes and equally affects the measured calcium concentration at different phases. Thus, the phase shift calculated here is robust against this experimental limitation.

We find that the calcium concentration approximately peaks when the radius is minimal and vice versa (figure 2(a)). The determined deviation from an anti-phasic relation is smaller than (figure 2(a)) and all four data sets show positive phase shifts (figure 2). Furthermore, the phase averaged signals (figure 2) reveal that the signal corresponding to the inner calcium concentration reaches its minimum earlier than the outer concentration.

Figure 2. Anti-correlated relation between radius and calcium signal. (a) The total concentration 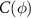, inner concentration , and outer concentration as a function of the phase of the contraction of the tube shows a relation which is close to anti-phasic, but with a clear positive shift meaning that the radius peak precedes the minimum in the calcium signal. (b) Phase relation of radius and calcium signal consistently indicates a nearly anti-phasic, positive shift. Data set A is the data set shown in (a).

Download figure:

To assess the contribution of potential auto-fluorescence or uneven Calcium Green-1 concentration in the tube cross-section, we consider the following case: Assuming the entire auto-fluorescent material is located in the tube walls and only contributes to the signal measured in the Calcium Green-1 channel, the ratiometric signal is shifted towards an anti-correlated relationship between the radius and calcium concentration (see also supplementary 3 and figure S5). Similarly, an accumulation of Calcium Green-1 bound to calcium in the tube cortex would shift the ratiometric signal in the same way. Thus, we regard the measured phase shift as a lower bound, and the true phase shift might be larger.

As calcium concentration interacts with the cortex, which is itself driving contractions that generate fluid flows that are shuttling calcium around, theoretical models help disentangle how calcium affects the cortex.

To investigate the phase relation for calcium acting as an inhibitor, we formulate a theoretical model. Note, that we here aim for the minimal amount of the assumptions to gain mechanistic insight on the qualitative predictions of the model rather than over-modelling for the pursuit of quantitative agreement with data. Thus, the model couples the contractile stress to the concentration of calcium, while the inflow of calcium depends on the stretch of the cortex following [23]. The model describes a tube consisting of a fluid phase and an enclosing visco-elastic cortex, where the active stress of the cortex is inhibited by the calcium concentration. At the same time, the calcium concentration is coupled to the stretch of the cortex.

The tube is radially symmetric, and, thus, the tube shape is fully described by the radius that depends on the position along the tube z and time t. The continuity equation in terms of the tube radius reads,

Radial deformations of the tube are written as , where is the rest radius.

The cortex stress σc is the cause of the pressure gradient along the tube and, thus, the cross-sectionally averaged flow velocity U reads,

The key assumptions of the model are the coupling of the cortex stress σc to the calcium concentration as well as the coupling of the capturing rate of calcium to the deformations of the tube ε. Specifically, in the model, calcium inhibits the contraction of the tube and flows in as the tube is contracted. The cortex stress is modeled by a passive visco-elastic part described by a Kelvin–Voigt model with an additional non-linear term and an active part that depends on the calcium concentration.

where E is the elasticity, κ the strength of the non-linearity, and η the viscosity of the cortex. is the cross-sectionally integrated calcium concentration with being its equilibrium value. For the active stress term, s is related to the slope of the tension at physiological concentrations and may be interpreted as the sensitivity to concentration changes. The parameter σ0 determines the amplitude of the tension.

The calcium dynamics reads,

The first term describes the transport of calcium along the tube governed by Taylor-dispersion [30, 31]. As calcium triggers the contractions of the tube, the inflow of calcium is dependent on the stretch of the cortex creating a feedback loop. Deformation-induced regulation in eukaryotic cells has been found experimentally [32–34]. Especially the knowledge about mechanosensitive calcium channels [35] motivates the source term. The relevant length scale of the deformation for the deformation-dependent calcium capturing is represented by εc . The parameters pc and dc determine the strength of the inflow and capturing, respectively. Notably, the cross-sectionally averaged calcium concentration and the radius of the tube are the properties we determine from the experimental data.

The rheological properties of the cortex determine how the cortex responds to stress. Thus, the elasticity and the viscosity in the Kelvin–Voigt model affect the relation of the tube radius to the calcium concentration. We consider two contrasting cases: A cortex with a high viscosity η yielding and low elasticity and a cortex with high viscosity and high elasticity E such that . To achieve that, the elasticity is set to and to , respectively, while the viscosity is unchanged.

The altered rheological properties of the tube cortex affect the phase shift between the full relaxation of the tube and the peak of the calcium concentration: For a cortex with a high elasticity (figure 3(b)), the phase shift is larger than for a cortex with a high viscosity (figure 3(d)). Thus, as the viscous term becomes more important relative to the elastic term in the Kelvin–Voigt model, the radius signal is delayed relative to the active tension. At low elasticity, the phase relation approaches the experimentally observed phase shift, but there remains a quantitative difference to the relation found experimentally which is closer to anti-phasic than the predicted one.

Figure 3. Theoretical model with an inhibiting calcium effect predicts a phase shift depending on the cortex properties, but smaller than . (a) In this model, calcium inhibits the active stress of the tube cortex leading to the deformation of the tube ε. Depending on the tube radius the overlap of actin in the cortex increases cortex stress when the tube radius is small leading to strong tube deformation which eventually triggers the inflow of calcium. (b) For a cortex with high elasticity the phase relation between the calcium and the radius is close to . (c) The cortex stress shows a shift of almost . (d) For a mainly viscous cortex the phase relation is shifted left towards the anti-correlated relation that is observed in the experimental data. (e) The cortex stress oscillation is shifted in the same direction relative to the cortex stress oscillation shown in (c).

Download figure: