Introduction Clinical background

Preterm birth is the main cause of neonatal deaths (about 35% of all cases) and accounts for 16% of child mortality under 5 years [UNICEF report; (1)]. The morbidity (2, 3) and mortality (4) rate increases with decreasing GA at the time of birth. To stratify the severity of preterm birth, three subgroups are defined: extremely preterm (< 28 weeks), very preterm (28–32 weeks), and late preterm (32–37 weeks) (WHO report; (5)). Globally, incidence rate of preterm birth for these subgroups is 4.1, 11.3, and 84.7%, respectively, (6) with an all-cause mortality incidence rate ratio of 1.91, 1.64, and 1.31, respectively, relative to the full-term birth (4). For extremely preterm born infants of 24–26 weeks GA, the chance of survival to 2 years is about 65–80% depending on GA (7).

Currently, medical care for premature infants is focused on supporting and monitoring temperature, respiration, cardiac function, oxygen saturation, and brain activity. However, supporting neonatal physiology may not be sufficient to treat premature infants. The transition from fetus to neonate requires a change in oxygen and nutrients source (lungs and gastrointestinal tract instead of placenta) and adaptation of the cardiovascular system (closing of shunts) (see Section Fetal cardiovascular physiology) (8). Therefore, this transition may result in life-long complications for premature infants when maturity of the organs has not been reached yet (9). These complications include respiratory, gastrointestinal, neurological, feeding, visual, and hearing problems (6, 10–13). Between 40 and 60% of the extremely preterm survivors experience major morbidity in the first year with about 75% when born at 23 weeks to about 45% when born at 26 weeks of GA (3). The review of (14) shows increased neuropsychiatric disorders for extremely preterm and very preterm compared with full-term born infants. Furthermore, an increase in moderate and severe disabilities at 18 years is seen by decreasing GA at time of birth from 5.6 and 3.7%, respectively, for full-term born infants, to 10.6 and 11.8%, respectively, for infants born at 24 weeks GA (15).

The short- and long-term health problems of these premature infants have enormous economical consequences. The initial hospital costs of live births are inversely associated with GA ranging from approximately $111,000 to $577,000 for 24 weeks to $900 to $7,000 for full-term infants (16). In addition, the estimated incremental costs of very and extremely preterm surviving to 18 years is substantial higher (~$96,000 and ~$147,000, respectively) compared with a full-term infant (~$35,000) (15).

The current healthcare system seems to have reached its limits regarding the support of neonatal physiology-based intensive care. Therefore, current research investigates a shift in medical care for extremely premature infants from supporting neonatal to remain fetal life ex utero in order to increase the chance of survival, reduce morbidity, and reduce the social economical costs (17–19). To achieve this, the transition from fetus to neonate needs to be postponed until organs have reached a sufficient level of maturity. This could be achieved with the development of a novel liquid-filled incubator for extremely premature infants, a PLS system (19–21). Such an incubator is designed to mimic the environment of the natural womb and is being developed to allow the fetal lungs to remain filled with liquid, while the umbilical cord is connected to an artificial placenta.

The PLS system will consist of an artificial placenta to supply nutrients and oxygen, a liquid-based environment with artificial amniotic fluid including an amniotic dialyzer, sensors to measure fetal vital signals, and a monitoring and model-based decision support system to interpret the signals and suggest interventions. All these components have to be tailored to the requirements of the PLS system (17). For instance, to avoid damaging of blood, no blood pumps should be used in the fetal-artificial placenta circulation (19), which implies that a low resistance, low volume artificial placenta is required. Furthermore, monitoring of the fetus should be possible despite the design choices for the system, e.g., regarding signal permeability through the PLS system walls.

Therefore, to develop and implement such a liquid-based incubator, different design choices have to be considered and knowledge of multidisciplinary fields have to be integrated into one system. A virtual representation of the PLS system could support this integration by testing and verifying scientific hypotheses, and similarly by predicting the interaction of mechanical components and their effect on the fetus. Ultimately, such a model can support clinical decision making by interpreting measured vital signals and estimating immeasurable but important parameters when the PLS system is introduced in the clinic. Furthermore, mathematical models could provide understanding of the underlying mechanisms to determine the physiological state of the fetus. Currently, the knowledge about the physiological state of the fetus is mainly based on non-invasive measurements, when anatomical and genetic disorders are ruled out. Ultrasound is used to measure growth, heart rate, and the amniotic fluid volume. When fetal growth restriction is suspected, Doppler ultrasound is used to measure blood velocities in the umbilical cord (22, 23) and/or one of the cerebral arteries (24) to assess Doppler indices. When the Doppler indices are abnormal, cardiotocography is performed to assess fetal heart rate and uterine activity. Bases on these findings, labor could be induced when the cardiotocogram is abnormal. Maternal blood pressure is measured to rule out hypertensive disease of pregnancy. These measurements are indirect data to determine whether placental capacity is sufficient in order to provide the fetus with enough nutrients and oxygen for growth and development. As all these measurements are clinically used to determine the physiological state of a fetus, it is of importance to understand the underlying mechanisms. For this, the use of mathematical models will be indispensable, not only as part of the development and implementation strategy of PLS system, but also as decision support tool during medical treatment. In the development phase, the digital twin will particularly be used to leverage our knowledge of the fetal physiology and to guide the development and implementation of a PLS system. To this end, the digital twin can be connected to a physical twin, i.e., a fetal manikin, to simulate fetal responses during training sessions. Once the PLS system has been implemented for clinical treatment, the digital twin model can also be used as decision support tool in clinical practice to predict the effect of interventions. For the development of the digital twin of a fetus in a PLS system, existing models are evaluated against the digital twin functional and technical requirements, which are specified in the next sections.

Functional requirements

The purposes of the digital twin required to support the development and implementation of a PLS system are:

1. Gaining knowledge: To develop a PLS system, extensive knowledge about the fetal physiology is necessary. However, this knowledge is (yet) insufficient mainly due to scarcely available data, as to protect mother and infant, data acquisition is limited by non- or minimal invasive tests during pregnancy. Hence, current data often consist of indirect measurements and/or animal data. Furthermore, the few invasive human fetal data available, have been derived from fetuses that required an intrauterine intervention. As a result, often assumptions and hypotheses are used to estimate the wellbeing of the fetus non-invasively. By testing these hypotheses, the digital twin should help gaining the necessary knowledge of the physiology of the fetus to create an optimal environment for fetal development.

2. Optimizing components: To analyze the interaction of the mechanical components of a PLS system with the fetus, the digital twin must be able to simulate the mechanical and fluid dynamic functioning of these components. Hence, the digital twin should be able to optimize the desired effect of the components on the fetal physiology.

3. Monitoring: When a PLS system is implemented in the clinic, the digital twin should be able to monitor and to interpret vital signals during a PLS system operation. These vital signals include heart rate, blood flow over the cardiac valves, cerebral and peripheral oxygen saturation, and blood pressure and flow in the important vessels (aorta, umbilical cord, and vena cava) and fetal cardiovascular shunts (ductus venosus, ductus arteriosus, and foramen ovale).

4. Decision support: The digital twin should serve as patient-specific decision support tool for clinicians. The tool should advice the user about the settings of a PLS system or even support interventions by fetal distress.

5. Training of clinicians: Before implementation of a PLS system, clinicians have to be trained to transfer a fetus from the natural womb to the system. For training purposes, the digital twin connected with a manikin can provide real-life simulation scenarios.

6. Digital twinning: For a mathematical model to be defined as digital twin, the mathematical model should be dynamically paired with the real-life fetus in the PLS system. In other words, the mathematical model should integrate the measurements of the fetal vital signals and provide decision support. The measurements of the vital signals include oxygen saturation in cerebral microcirculation, estimation of fetal weight, fetal electrocardiogram, and blood flow and pressure through the umbilical cord.

Technical requirements

To satisfy the above-mentioned functional requirements, the digital twin should meet technical requirements described in this paragraph. The cardiovascular system is the transport system for oxygen, nutrients, and metabolic waste products. Hence, it is a key facilitator of growth and development. In addition, the PLS system sustains fetal physiology. Therefore, this paper and also the set of requirements in this section are mainly focused on the fetal cardiovascular system including oxygen transport and fetal growth. Hence, the nutrient utilization and hormone pathways are excluded from this study.

1. Cardiovascular system: The digital twin should describe the pressure and flow relations in the important vessels in the cardiovascular system to analyze the hemodynamic state of the fetus. These vessels include cerebral and umbilical vessels, aorta, vena cava, and shunts (ductus arteriosus, ductus venosus, and foramen ovale).

2. Closed-loop: A closed-loop of the prenatal circulation is required to simulate the entire fetal cardiovascular system including the shunts and venous return.

3. Pulsatile driving force: The digital twin will be verified on available clinical data. These data consist mainly of blood velocities measured by Doppler ultrasound, fetal heart rate, and growth. To simulate blood velocity waves, the cardiovascular system should be provided with a pulsatile pressure or flow source in physiological or pathological range. This could be generated by a fetal cardiac contraction model or a prescribed profile.

4. Wave propagation and reflections: In order to propagate these pulsatile pressure and flow waves throughout the entire cardiovascular system, wave propagation and reflections of pressure should be incorporated in the digital twin. Furthermore, the shape of the pressure and flow waves have potential diagnostic value.

5. Maternal-fetal gas exchange: Maternal-fetal gas exchange takes place in the placenta. Placental insufficiency could lead to lower oxygen saturation in the fetus. Therefore, it is of importance that the digital twin contains maternal-fetal gas exchange mimicking oxygen transport during physiological and pathological conditions.

6. Baro- and chemoreceptor reflex: Baro- and chemoreceptor reflex are part of the regulatory system to maintain homeostasis. Furthermore, redistribution of the cardiac output when the fetus is in distress is regulated by these reflexes. Therefore, the digital twin should contain baro- and chemoreceptor reflexes. Noteworthy, the regulatory system of extremely premature infants is different from adults and full-term fetuses (25).

7. Fetal growth: The fetus growths from about 700 g at 24 weeks to 1,200 g at 28 weeks GA (26). Hence, the digital twin has to be able to predict fetal growth and its impact on the circulation during physiological and pathological conditions.

8. Real-time: Computational time should be pseudo-real-time such that the digital twin can be used as clinical decision support tool when a PLS system is introduced in the clinic. The digital twin should be able to run in a local clinical setting as patient data cannot leave the hospital and, hence, the digital twin should be integrated in an advanced personal computer or dedicated workstation that can be located on the ward. Therefore, 3D modeling is most likely not feasible. However, when a particular part of the digital twin requires 3D modeling to properly describe its function, meta-models should be developed allowing the desired order of detail with less computational expense.

These requirements demand for a computational model that is multiscale and multilevel in order to simulate different length and time scales and complexity. To allow such a complex combination of multiscale and multilevel modeling approach and to remain flexibility to extend, reduce, or adapt parts of the model, it needs a modular arrangement. Figure 1 shows an example of a modular arrangement. In this example, the fetal cardiovascular model is a closed-loop model (2. closed-loop) containing the description of the vessels (1. cardiovascular system) driven by a pulsatile force (3. pulsatile driving force) creating realistic pressure and flow waves (4. wave propagation and reflections). The resulting pressure, flow, and volume in the vessels are the input of the metabolism model (not included in this study) and maternal-fetal gas exchange model (5. maternal-fetal gas exchange). Based on the oxygen saturation resulting from the maternal-fetal gas exchange model, feedback is provided by the regulatory system model (6. baro- and chemoreceptor reflex) to the fetal cardiovascular model by changing the peripheral resistance and heart rate accordingly to the fetal needs. Furthermore, oxygen and nutrients are necessary for fetal growth (7. fetal growth) leading to adaptation of parameter settings in the cardiovascular, distribution, and regulatory system models. Section Model integration elaborates on the integration of model functionalities on multiscale and multilevel.

FIGURE 1

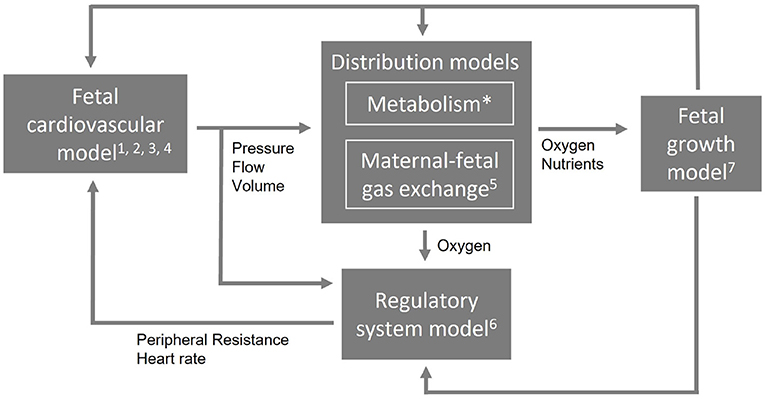
Figure 1. An example of a modular arrangement. The numbers refer to the numbering of the technical requirements (Section Technical requirements). The first four requirements are applicable to the cardiovascular model. Metabolism is not included in this study (*) and the computational time applies to the entire model (not shown).

Existing fetal circulatory mathematical models

Part of the current research is based on the complete circulation implemented as a LPM to describe global distributions of flow, volume, and pressure [e.g., (27–31)]. Others are focusing in more detail, by means of 1D or 3D modeling, on a part of the circulation. For instance, to evaluate forward and reflected waves or pulsatile flow in the umbilical artery [e.g., (32–38)], arterial side [e.g., (39–42)], aortic coarctation [e.g., (43)], umbilical vein [e.g., (44)], or the feto-placental arterial network [e.g., (45, 46)]. In order to simulate a complex system like the fetal cardiovascular circulation with oxygen transport and fetal growth, we are not solely looking for global distributions of blood volume, pressure, and flow or parts of the fetal physiology, but for a single model that describes all requirements (Sections Functional requirements, Technical requirements). Within a single model, the fetal cardiovascular circulation can be assessed as an entity and not as isolated parts. Therefore, the digital twin should integrate all necessary functionalities of existing mathematical models in a coherent description of the fetal cardiovascular system including fetal growth and oxygen transport.

Aim

The aim of this paper is to provide a review evaluating how existing models meet (part of) the digital twin model requirements in order to propose a strategy for the development of this digital twin of a fetus in a PLS system.

Outlook

Building upon the predefined requirements (Sections Functional requirements, Technical requirements), the fetal cardiovascular physiology (Section Fetal cardiovascular physiology) and the physics to describe this physiology (Section 0D and 1D circulatory models) are presented. Subsequently, the search query is defined as well as the assessment method for the identified models (Section Assessment of existing models). The literature survey leads to an overview of 0D models (Section 0D models) and 1D models (Section 1D models). Next, these mathematical models are discussed (Section Discussion), while considering the technical requirements (Section Technical requirements) and how the models can be integrated. In addition, the model proposal for a digital twin of a fetus in a PLS system (Section Model proposal: A digital twin of a fetus in a PLS system) is presented and the limitations of this study are given. Finally, a conclusion summarizes the insights obtained and their implication for the development of a digital twin of a fetus in a PLS system (Section Conclusion).

Fetal circulatory models Fetal cardiovascular physiology

The fetal cardiovascular system (Figure 2A) deviates from the adult cardiovascular system (Figure 2B) as the fetus receives oxygen and nutrients from the placenta instead of the lungs and gastrointestinal tract, respectively. The oxygen- and nutrient-rich blood from the placenta flows via the umbilical vein to the portal sinus and the ductus venosus. The portal sinus supplies the liver with oxygen- and nutrient-rich blood via the portal vein. The oxygen- and nutrient-rich blood in the ductus venosus enters the inferior vena cava and flows into the right atrium. In the right atrium, oxygen- and nutrient-rich blood flows preferentially to the left atrium via the foramen ovale. A smaller part of the right arterial blood flows to the right ventricle. In the right ventricle, a small part flows to the pulmonary arteries to supply the lungs. The rest of the blood mixes with the aortic blood via the ductus arteriosus. Blood from the foramen ovale and pulmonary veins in the left atrium flows into the left ventricle to the rest of the organs and enters ultimately in the two umbilical arteries that brings the blood back to the placenta for nutrient uptake and re-oxygenation. After birth, the cardiovascular system undergoes multiple changes to switch from placental to pulmonary oxygenation. This cascade is initiated by, among other things, the first breaths after birth. As a result, the shunts (ductus venosus, foramen ovale, and ductus arteriosus) will close in the following hours. In addition, the umbilical cord is cut, thus causing closure of the umbilical vessels. These changes all contribute to the transition from fetal to neonatal cardiovascular physiology. For an extensive description of the fetal cardiovascular system, the reader is referred to (8).

FIGURE 2

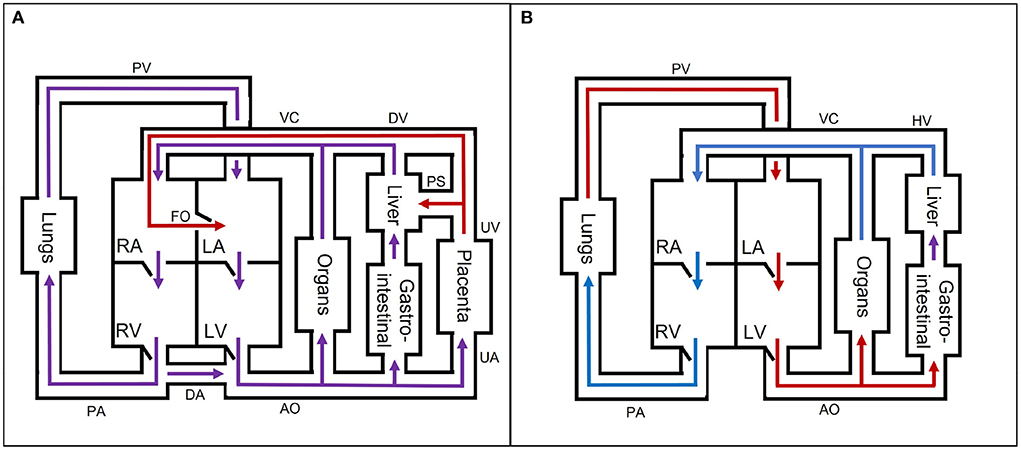
Figure 2. A simple schematic overview of the (A) fetal and (B) neonatal circulation with oxygen- and nutrient-rich (red), oxygen- and nutrient-poor (blue), and oxygen- and nutrient-rich and -poor mixed (purple) blood flow direction. AO, aorta; DA, ductus arteriosus; DV, ductus venosus; FO, foramen ovale; HV, hepatic veins; LA, left atrium; LV, left ventricle; PA, pulmonary arteries; PS, portal sinus; PV, pulmonary veins; RA, right atrium; RV, right ventricle; UA, umbilical arteries; UV, umbilical vein; VC, inferior and superior vena cava. The block “organs” represents all other organs, which are not separately mentioned in the figure.

0D and 1D circulatory models Cardiovascular system

The motion of blood through the fetal cardiovascular system is governed by the Navier-Stokes equations. These partial differential equations are based on the balance of mass (1) and momentum (2). When assuming an incompressible fluid, the Navier-Stokes equations are given by:

∂ρ∂t+∇·(ρu)=0,    (1) ∂∂t(ρu)+∇·(ρu⊗u)=-∇p+∇·τ+ρf,    (2)

with ρ the blood density [gm3], u the blood velocity [ms], p the hydrostatic pressure [Pa], τ the shear stress tensor [Pa], and f body accelerations [ms2], such as gravitational forces. When (1) and (2) are integrated over the cross section A, the following formulas are obtained:

∬A(t)[∂ρ∂t+∇·(ρu)]dA=0,    (3) ∬A(t)[∂∂t(ρu)+∇·(ρu⊗u)]dA=∬A(t)[-∇p+∇·τ+ρf]dA.    (4)

1D wave propagation models can subsequently be obtained after applying Reynolds transport theorem (47), assuming cylindrical symmetry, and applying no-slip condition on the wall. This results in a blood velocity predominantly along the longitudinal or central axis (z-direction) that varies perpendicular to this axis (r-direction). In other words, velocity is zero with respect to the wall velocity. As the velocity is predominantly in z-direction, the velocity in r-direction and circumferential direction (θ-direction) is neglectable. Hence, the pressure and flow in the vessels are dependent on the z-direction and time (p(z, t) and q(z, t), respectively). Subsequently, (3) results in (5) by dividing by ρ and multiplying by A:

∂A∂t+∂q∂z=0,    (5)

with q the blood flow. Using Reynolds transport theorem, (4) results in:

∂q∂t+∂∂z(δq2A)=Aρ(−∂p∂z+2rτz)+Afz,    (6)

with τz the wall shear stress [Pa], fz body accelerations [ms2], δ a variable to define the velocity profile [−] (48, 49), r the radius. Subsequently, to solve (5) and (6), a constitutive relation has to be defined to give a relation between p and A. For elaborate description of the derivations, the reader is referred to the review of (48). When (5) and (6) are integrated over the length z, formula to describe 0D models are derived:

∫z(t)[∂A∂t+∂q∂z]dz=0,    (7) ∫z(t)[∂q∂t+∂∂z(δq2A)]dz=∫z(t)[Aρ(−∂p∂z+2rτz)+Afz]dz.    (8)

Substituting the area compliance CA=∂A∂p in (7) results in:

C∂p∂t+Δq=0,    (9)

with C the vessel compliance [m3Pa] (C = CAΔz). When the non-linear convection term (∂∂z(δq2A)) and the external forces (fz) are neglected and the viscous term (τz) is approximated with Poiseuille shear stress, a 0D formulation of the 1D momentum balance (6) is derived:

L∂q∂t=-Δp+Rq,    (10)

with L the inertia [Pa·s2m3] and R the resistance [Pa·sm3].

Pulsatile driving force

The models with a pulsatile input contain a fetal cardiac module (time varying elastance model or one fiber model) or a prescribed flow or pressure profile. The time varying elastance model describes the pressure in a cardiac cavity (pcav) with a variable compliance, which is based on the minimum (Emin) and maximum elastance (Emax) of the heart muscle in [Pam3] and the instantaneous volume of the cavity Vcav (50). The cavity pressure is given by:

pcav(t)=((Emax-Emin)a(t)+Emin)(Vcav(t)-Vcav,0),    (11)

with Vcav, 0 the cavity volume at zero pressure [m3] and a(t) the time dependent activation function of the contraction with a value between 0 and 1 [−]. The underlying phenomena of cardiac contraction are better described by the one fiber model, as this model relates pcav to the cavity volume Vcav, myocardial wall volume (Vwall), and myocardial fiber stress (σf), with the latter depending on the fiber length, activation time, and sarcomere shortening velocity (51, 52):

pcav(t)=13σfln(1+(VwallVcav)).    (12)

This model is based under the assumption that the stress in the myocardial fibers is homogeneous, which allows modeling of a single-fiber.

Maternal-fetal gas exchange

The transport of oxygen expressed as the rate in change of oxygen in an organ (d(cO2V)dt) is the sum of the convective transport to and from the organ (QC), the metabolic consumption of the organ (QM), and diffusive exchange (QD) (53):

d(cO2V)dt=QC+QD-QM,    (13)

with V the volume of the organ [mL], the oxygen fluxes (Qc, QM, and QD) in [mLo2s], and cO2 the oxygen concentration [mLo2mLblood].

Assessment of existing models

Section Technical requirements mentioned the technical requirements of the digital twin of a fetus in a PLS system. To find eligible models that (partly) satisfy the technical requirements, a literature search1 is executed on fetal cardiovascular models including fetal growth and oxygen transport. Subsequently, each paper is assessed based on the requirements as summarized in Table 1. For the fetal growth requirement, the age and/or weight is included as well. Furthermore, pulsatility can be obtained by a cardiac model mimicking the contraction of the heart, such as the TVEM (50) and OFM (51) or by a prescribed flow or pressure profile (PP). The computational time is not included as many papers did not mention this. This study is limited to models in 0D and 1D, and the identified models are organized accordingly. For an elaborate description about the contribution of 0D and 1D modeling to describe cardiovascular systems, the reader is referred to (54).

TABLE 1

Table 1. Technical requirements and their assessment.

0D models

Describing the fetal cardiovascular system as a 0D model is intensively explored in literature. These models mostly describe the cardiovascular system as analog of an electrical circuit. In this study, two different 0D model types are described; lumped parameter models and transmission line models. A lumped parameter model consists of several compartments describing the microcirculation of an organ, a vessel, or part of a vessel. The number of compartments depends on the research question. As homogeneity is assumed within a compartment, global distributions of flow, pressure, and volume can be examined. Typically, the local effects of wave propagation and reflections in larger vessels can not be analyzed in the coarse representation of the cardiovascular system. Nevertheless, uniform distribution of the variables still provide a general overview of the functionalities of the fetal cardiovascular system. Furthermore, lumped parameter models are used to provide boundary conditions for higher dimensional models. Transmission line models are distributed lumped parameter models, meaning that the compartments are described with multiple segments assuming non-homogeneity within a compartment. Therefore, transmission line models, in contrast to lumped parameter models, allow simulation of forward and backward pressure and flow waves. To capture those waves, as a rule of thumb, the length of these segments should be 10 times smaller than the smallest wavelength, as a pressure signal has approximately a maximal frequency of 10 Hz (55). The next sections provide an overview of the currently existing lumped parameter and transmission line models. Supplementary Table 1 gives an overview of the assessment based on the technical requirements.

Lumped parameter models

Huikeshoven et al. (27) developed the first closed-loop fetal cardiovascular lumped parameter model containing contracting ventricles based on behavior of sarcomeres, passive atria described with a fixed compliance and resistance, and six compliant vascular compartments. This model was used to understand the behavior of the fetal heart (including its shunts) by changing the arterial pressure, blood volume, heart rate, and afterload (27) and the effect of partial closure of the ductus arteriosus (56). Although the parameters of this model are based on data from fetal lambs, the framework of this model is the basis of multiple mathematical research studies of the fetal cardiovascular circulation. In 1985, Huikeshoven et al. (57) extended their model to 16 compartments and included oxygen transport based on fetal sheep data, but simplified the heart to two chambers and described their function with a cardiac function curve. In addition, they scaled the parameters to human fetal cardiac output, while remaining the same distribution of blood flow to evaluate fetal oxygen consumption (28). One decade later, the first closed-loop lumped parameter model was developed that allowed interpretation of clinical data by verifying parameters of the model on Doppler velocity waveforms of healthy full-term fetuses (29).

In the next decades, the hemodynamics of growth and transition from fetus to neonate were simulated for healthy fetuses (30, 31, 58–60). Pennati and Fumero (59) applied scaling laws to their model (29) in order to evaluate the effect of growth on the pulsatility index in several vessels, on the velocity across the valves, and through the shunts during pregnancy (59). In 2010, Sa Couto et al. (58) studied the hemodynamic effects of the transition from fetus to neonate including the effect of clamping the umbilical cord. This model builds on previously published models of the cardiovascular system of neonates (61–63). With a similar research question and inspired by (29), Yigit et al. simulated the effect of the transition and the effect of cord clamping on the hemodynamics and oxygen saturation of a full-term (30) and preterm fetuses (31). The latter was achieved by scaling the model on GA (64). Similarly, Munneke et al. (60) used CircAdapt (65) to mimic this transition. While the above mentioned models use a time varying elastance model, CircAdapt contains a one fiber model to simulate the contraction of the heart. These models (30, 31, 58–60) show that lumped parameter models can be used to simulate specific events (e.g., transition from fetus to neonate or fetal growth) and evaluate the new distribution of blood flow, pressure, volume, and oxygen saturation. However, when evaluating the model results, it should be taken into account that only spatial average effects can be modeled and that wave propagation and reflections are not taken into account, which could affect the pulsatility index of the flow in the arteries and, in particular, the umbilical arteries.

During the same time period, the effect of labor on the cardiovascular system including oxygen transport has been an important topic of several research papers. Especially, the effect on the fetal heart rate, because the timing of fetal heart rate decelerations give an estimation of the physiological state of the fetus and it can be measured by the means of cardiotocography. Van der Hout-van der Jagt et al. (52) developed the first model to investigate the underlying mechanisms of the effect of labor on fetal heart rate focusing on early decelerations (52) and late decelerations (66). In addition, van der Hout-van der Jagt et al. investigated fetal oxygenation changes caused by umbilical cord compression (67) and maternal hyperoxygenation affected by labor (68). These models contain the mother and fetal cardiovascular circulation connected through the placenta, fetal-maternal gas exchange (53), and baro- and chemoreceptor reflex (69). Jongen et al. reduced the complexity of these models (52, 66, 67) to limit the number of indirect measured fetal parameters (70) and to study umbilical cord compression during contractions of the uterus (71). In addition, Wang et al. (72) extended the model of (52) to simulate glucose, lactate, and pyruvate to detect fetal acidemia during labor. As far as we know, this model with all these phys