MAP-SNN: Mapping spike activities with multiplicity, adaptability, and plasticity into bio-plausible spiking neural networks

, and membrane resistance R ∈ . By simulating discrete models in Figure 3, we obtain the findings presented in the Figure 7. The results obtained under various τ and R confirm the derivation presented in Section 2.2.3. First, the Standard Numerical Model yields perfectly stable results, and the number of recorded spikes does not vary with Δt. Comparing Figures 7A,B, the Simplified Numerical Model is a good approximation of the Standard Numerical Model when R is large; comparing Figures 7A,C, the Linear Mode of the MSP is closer to the Standard Numerical Model as τ increases. Notably, these findings indicate that Soft-Reset Model initially displays performance that is highly close to Linear Mode, but is restricted by binary transmission when Δt is large, where the number of recorded spikes is inversely proportional to Δt, indicating that the extension of the SSP to the MSP is rational.

FIGURE 7

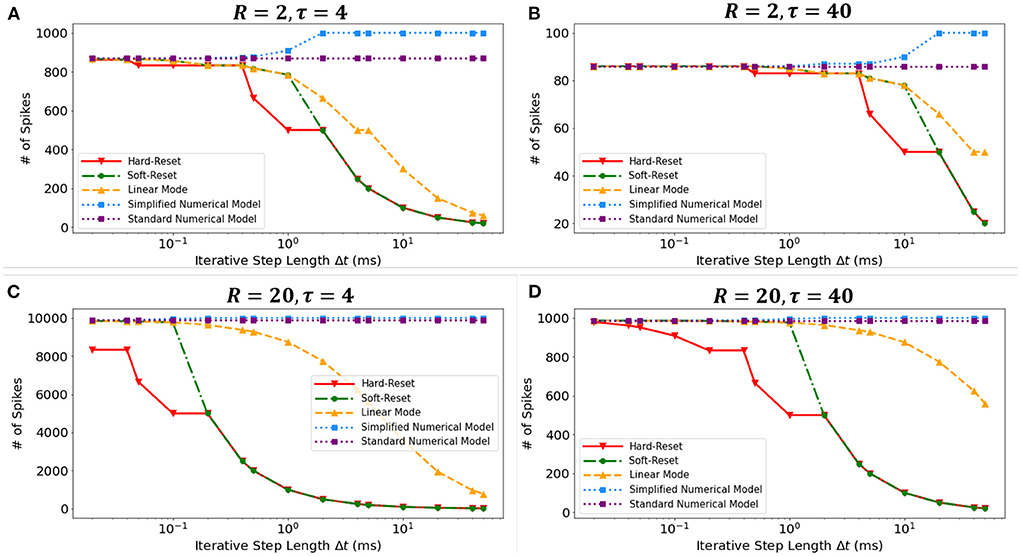
Figure 7. The numbers of spikes via Δt with different discrete models. Four experiments with different τ and R: (A) R = 2Ω, τ = 4ms, (B) R = 2Ω, τ = 40ms, (C) R = 20Ω, τ = 4ms, (D) R = 20Ω, τ = 40ms.

3.2. Classification of neuromorphic datasets

To demonstrate the reliability of our approaches, we train our SNN models with spike-based datasets for image and sound classification and compare the achieved error rates with related works on SNN algorithms.

3.2.1. Experiment setting and parameters initialization

The proposed model is built on the deep learning framework, PyTorch (Paszke et al., 2019), and the weights are initialed using the default Xavier Normal (Glorot and Bengio, 2010) method. Besides, we use Adam as the optimizer and Cross-Entropy as the criterion during training. Hyperparameters of experimental settings are shown in Table 1. We built fully connected networks for classification as the Multilayer Perceptron (MLP) structure.

TABLE 1

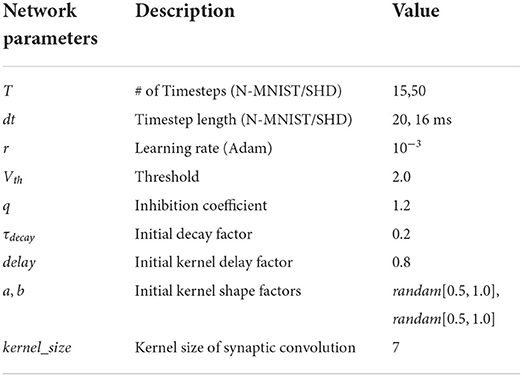
Table 1. Hyperparameters setting.

3.2.2. Neuromorphic image dataset

N-MNIST (Orchard et al., 2015) is a neuromorphic version of MNIST digits, which contains 60,000 train samples and 10,000 test samples aligning with MNIST. The samples of N-MNIST are event-based spike signals captured by recording MNIST images displayed on an LCD screen using Dynamic Vision Sensors (DVS) mounted on a moving platform. The N-MNIST images record overall 300ms frames and have two channels that separately record brighter and darker brightness changes. We process the two channels in parallel with two groups of 400 hidden neurons, where the network architecture is (2 × 1156)−(400+400)−10.

3.2.3. Neuromorphic sound dataset

Spiking Heidelberg Digits (SHD) (Cramer et al., 2020) is a spike-based speech dataset consisting of 0–9 spoken digits recordings in both English and German. The audio recordings are converted into spikes using an artificial inner ear model, transforming into temporal structures with 700 input channels. There are 8156 train samples and 2,264 test samples in SHD, and each of them lasts for at most 800 ms. SHD requires multiple layers to fit. Therefore, we built the architecture of 700−400−400−20 with two hidden layers of 400 neurons.

3.2.4. Error rate comparison

We compare the obtained model performance with state-of-the-art SNN models, The results of N-MNIST are in Table 2 and SHD is in Table 3, including ablation experiments with MSP and SFSRM alone. The experimental results show that MAP-SNN can decrease the error rate by 0.16% on N-MNIST and 1.30% on SHD, which has achieved the highest performance among SNN-based algorithms under the same MLP structure. Furthermore, we observe that MSP and SFSRM can independently improve the model accuracy and be combined for significantly better performance, which supports the complementarity of MAP properties.

TABLE 2

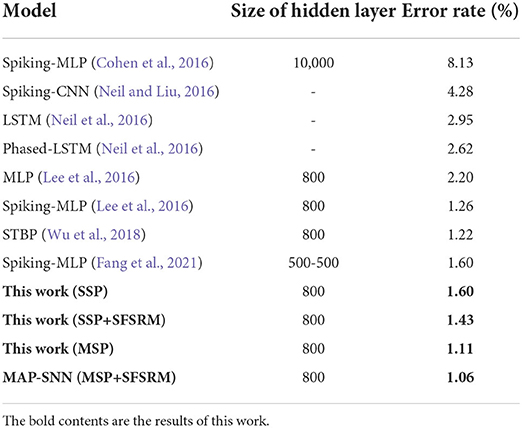
Table 2. Performance of different algorithms on N-MNIST.

TABLE 3

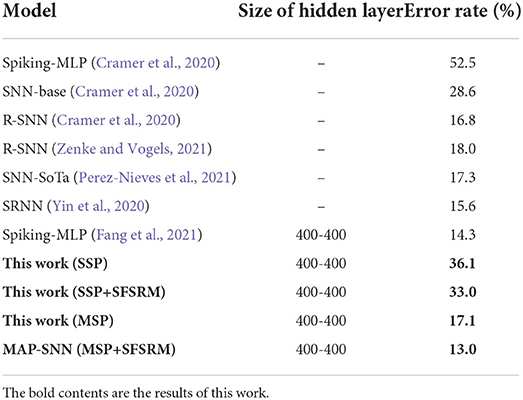
Table 3. Performance of different algorithms on SHD.

3.2.5. Visualization results

To help understand the signal transmissions of SNNs and highlight the difference between the MSP and the SSP, we derive the spike raster plot of an SHD sample. The network structure consists of two hidden layers of 700 − 400 − 400 − 20. The plot shows the neural spike activities in layers on the 800-th SHD training sample with label 0 in Figure 8. The horizontal and vertical axes indicate the time interval and the indices of spiking neurons in layers. In detail, we implement the SSP based on STBP (Wu et al., 2018) for comparison with the proposed MSP. In Figure 8B, it is observed under MSP that spike activities are more concentrated in the temporal dimension, while there are fewer nearby sparse spikes in deep layers (Layer 2 and Layer 3). In contrast, Figure 8C shows that the spike channels of Layer 2 are almost full, which is because the neurons under SSP are “encouraged” to keep fire to maintain signal integrity within restricted binary signals.

FIGURE 8

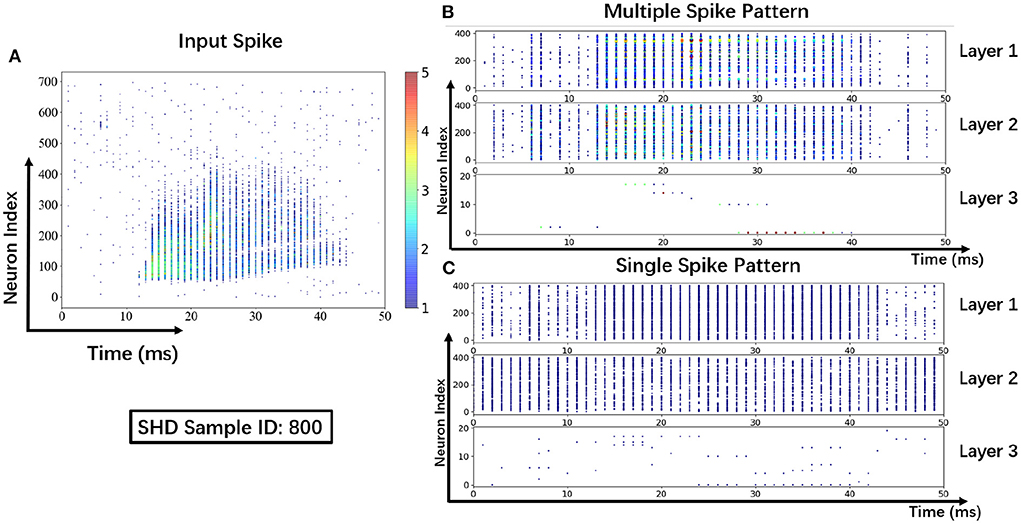
Figure 8. Spike raster plot: Visualization of spike transmission on SHD sample. (A) Input spikes. (B) Spike transmission in multiple spike pattern. (C) Spike transmission in single spike pattern.

3.3. Control experiments and performance analysis

To explore the potentials of the proposed MSP, SFA, and SFSRM, we carry out control experiments on N-MNIST and SHD datasets and discuss the impacts of MAP properties on improving model performance.

3.3.1. The impact of multiplicity on discrete iteration

The selection of minimal iterative step lengths Δt influences model performance in the discrete iterative models. For the sake of completeness of the analysis, we analyze this instability in the ablation experiments by building control experiments under MLP architecture with different iterative step lengths, as shown in Figures 9A,B. The experiments are based on N-MNIST and SHD, respectively, where the unified network structure is (2 × 1156)-200-10 on N-MNIST and 700-400-20 on SHD. With the MAP properties, the error rates of the model have been significantly improved. Compared with benchmark SSP, our MAP-SNN with the combination of MSP and SFSRM reduces error rates among different iterative step lengths by the range of (1.0, 2.8%) on N-MNIST, and (19, 41%) on SHD, which demonstrates the reliability of the proposed methods. Furthermore, the model trained with MSP keeps almost constant error rates across different Δt, supporting that multiplicity alleviates the discretization problem and improves the model stability over time-iteration with different iterative step lengths.

FIGURE 9

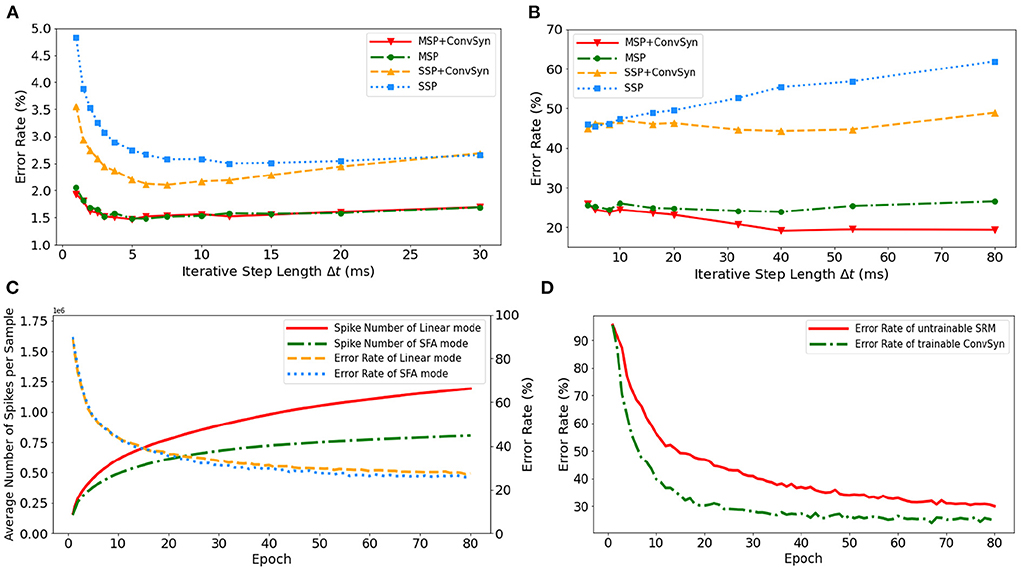
Figure 9. Experimental results. (A) Error rate curves among different iterative step lengths on N-MNIST. (B) Error rate curves among different iterative step lengths on SHD. (C) Control experiment of spike frequencies between SFA and Linear modes on SHD. (D) Control experiment of synaptic plasticity for performance improvement on SHD.

3.3.2. The impact of adaptability on spike efficiency

To demonstrate the effectiveness of SFA in spike reduction, we establish a set of controlled experiments on the SHD dataset with the 700-400-20 MLP structure. Figure 9C shows the error rates and spike numbers in the training process of models in both SFA mode and Linear mode. The experimental results show that SFA effectively suppresses spike activities by 1.48 × times while slightly improving model accuracy by 1.52%. In this case, the reduced signal transmissions helpfully decrease the amount of computation in synapses, which will help save the power consumption of neuromorphic hardware based on spike transmissions.

3.3.3. The impact of plasticity on feature extraction

To highlight the importance of plasticity for feature extraction, we set up a control experiment to compare the SRM with and without the plasticity, as shown in Figure 9D. The untrainable SRM refers to the fixed SRM (the parameters fixed after initialization) and the trainable SFSRM refers to our proposed method in Section 2.4. The experiment is set on the SHD with the 700-400-20 MLP structure, where the SRM or SFSRM is inserted on 400 hidden neurons. Figure 9D shows the changes in model error rate and loss during the training epoch. The experimental results show that the plasticity allows the model to converge faster by 4.2% and reduces the error rate by 15.6% during epoch [10, 80]. This demonstrates the advantage of SFSRM in temporal feature extraction. We conclude that plasticity helps shorten the training process of models and improve the model's performance.

4. Discussion

In this work, we refer to the Multiplicity, Adaptability, and Plasticity (MAP) properties and model spike activities with Multiple-Spike Pattern (MSP), Spike Frequency Adaption (SFA), and State-Free Synaptic Response Model (SFSRM) that improve BP-based methods with better performance. For the spiking neural models, the existing methods rely on the neurons with the single-spike pattern (SSP) that only outputs the binary events (Lee et al., 2016; Wu et al., 2018; Cheng et al., 2020), introducing discrepancies between the discrete iterative simulation and biological network. To mitigate this discrepancy due to time discretization, we propose an MSP spiking neural model that supports the neurons to output the number of spike events. We set up the control experiments on neuromorphic datasets and tested SSP and MSP in the same MLP architecture. The results demonstrate that the SSP is sensitive to the selection of iterative time step Δt, while the MSP is more robust under different time steps Δt compared with the SSP, as shown in Figures 9A,B. Considering the smaller number of simulation timesteps and lower inference latency, the spiking neurons with multiple thresholds are proposed in recent works (Chowdhury et al., 2021; Xu et al., 2021), which refer to the linear mode of MSP implementation. The spike activity increases linearly as the increase of input currents in such linear mode MSP. More spike activities require more energy for spike transmission and subsequent operations. While a biological neuron fires with a reduced frequency over time under a constant stimuli (Benda and Herz, 2003). Therefore, the SFA mode was implemented under the MSP to reduce spike activities while keeping on the model accuracy shown in Figure 9C. Some published works have applied the SRM model in SNNs to capture the spike temporal information and thus achieved high performance (Jin et al., 2018; Shrestha and Orchard, 2018). However, they restrict the shape parameters inside the kernel function and need to expand the kernel among temporal domains to do the calculation step by step. In order to enrich the model representation power and make the SRM more compatible in deep frameworks, we propose to substitute the iterative calculation with convolution operations and allow all parameters inside the kernel to be learned for plastic synapses.

The implementability of the proposed MAP-SNN is a major concern. State-of-the-art neuromorphic chips, such as Tianjic (Pei et al., 2019), Darwin (Ma et al., 2017), and Loihi (Davies et al., 2018), support the single-spike pattern directly. The MAP-SNN model with a generalized definition is feasible to perform the on-chip inference on Tianjic Chip with proper hardware configuration. In detail, the neural models of multiple-spike patterns with SFA mode can be simplified at the hardware level by pre-setting a lookup table to determine the number of spike activities based on the value of the current membrane potential. Besides, in the axonal process of spike traveling, the Tianjic chip with ANN-SNN hybrid design can compatibly perform the integer transmission, supportive of the multiple-spike pattern. Further, at the axonal terminal, the state-free synapses are implemented by the low-pass filters, which transform the spike activities into synaptic currents. We believe that algorithms and hardware can be developed in tandem. The improvements in algorithms may also inspire the hardware design. The feasibility of MAP-SNN on Tianjic provides a potential development perspective for both spike-based algorithms and neuromorphic hardware.

The aforementioned discrete models (Figure 3) have great numerical calculation accuracy in simulation and inference, which may be used in the ANN-SNN conversion approach to narrow the gap between analytical and numerical solutions, as well as reduce network latency through time compression; this is an area worthy of further exploration in the future.

In conclusion, this work demonstrates the potency of effectively modeling spike activities, revealing a unique perspective for researchers to re-examine the significance of biological facts.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: the datasets SHD/N-MNIST for this study can be found in the https://zenkelab.org/resources/spiking-heidelberg-datasets-shd/ (Spiking Heidelberg Datasets), and https://www.garrickorchard.com/datasets/n-mnist (Neuromorphic-MNIST).

Code availability statement

The source code of MAP-SNN can be found in the Github repository https://github.com/Tab-ct/MAP-SNN.

Author contributions

CY proposed the idea. CY and YD designed and did the experiments. CY, MC, and AW wrote the manuscript, then GW, AW, and EL revised it. AW directed the projects and provided overall guidance. All authors contributed to the article and approved the submitted version.

Funding

This work was supported in part by the Fundamental Research Funds for the Central Universities under Grant 2-2050205-21-688 and in part by the Zhejiang Provincial Natural Science Foundation Exploration Youth Program under Grant LQ22F010011.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adibi, M., Clifford, C. W. G., and Arabzadeh, E. (2013). Informational basis of sensory adaptation: entropy and single-spike efficiency in rat barrel cortex. J. Neurosci. 33, 14921–14926. doi: 10.1523/JNEUROSCI.1313-13.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

Bellec, G., Salaj, D., Subramoney, A., Legenstein, R., and Maass, W. (2018). “Long short-term memory and learning-to-learn in networks of spiking neurons,” in Advances in Neural Information Processing Systems 31, eds S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Curran Associates, Inc.). Available online at: https://proceedings.neurips.cc/paper/2018/file/c203d8a151612acf12457e4d67635a95-Paper.pdf

Google Scholar

Bellec, G., Scherr, F., Subramoney, A., Hajek, E., Salaj, D., Legenstein, R., et al. (2020). A solution to the learning dilemma for recurrent networks of spiking neurons. Nat. Commun. 11, 3625. doi: 10.1038/s41467-020-17236-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Cheng, X., Hao, Y., Xu, J., and Xu, B. (2020). “LISNN: improving spiking neural networks with lateral interactions for robust object recognition,” in IJCAI, 1519–1525. doi: 10.24963/ijcai.2020/211

More from this channel

MAP-SNN: Mapping spike activities with multiplicity, adaptability, and plasticity into bio-plausible spiking neural networks

留言 (0)