1 Introduction

Understanding the human processing of multi-sensory stimuli in relation to attention has been of great interest in the last decades (De Winne et al., 2022). Indeed, detecting cognitive states and skills can help improve adaptive learning, in which the learning material and pace are adjusted to match some collected data about learners during a learning task (Mohamed et al., 2018). Moreover, identifying biomarkers that can be used to monitor attention, pleasure and reward, and understanding the relationship between these biomarkers and fine-tuning of stimuli (sound, image, rhythm) can enhance the interaction between humans and artificial intelligence (AI) agents, which is still lacking the degree of engagement and entrainment that characterizes interaction between humans. Such advances in human-centered AI approach open a wealth of applications in public security, health, revalidation, communication and information sharing, entertainment, etc. Some examples include driver fatigue detection (Wan et al., 2013), rhythmic auditory stimulation to help Parkinson's patients improve their gait characteristics and reduce the risk for falling (Moens et al., 2017), or music systems for synchronization (Moens et al., 2010) and gait retraining (to prevent running-related injuries; Van Dyck et al., 2015) which could be improved by selecting the best rhythmic or music stimulus at the right moment.

A promising methodology for the automated collection of data during a mental task includes the use of bio-sensors that could measure subjects' emotions, attention, and engagement in a non-invasive and non-intrusive way (Mohamed et al., 2018). In this work, we focus on capturing human attention from electroencephalography (EEG) bio-signals. EEG data measures oscillatory electrical brain activity at the macroscopic scale with high time resolution (Speckmann et al., 2011; Yu et al., 2016). EEG has been shown to have a strong potential to provide biomarkers for diagnoses in many neuropsychiatric disorders (da Silva, 2013; Yu et al., 2016), including attention deficit hyperactivity disorder (ADHD; Lubar, 1991; Loo and Barkley, 2005; Liu et al., 2015; Janssen et al., 2017; Kiiski et al., 2020), but also as indicators of attention during different visual and cognitive tasks (Mulholland, 1969; Ray and Cole, 1985; Harmony et al., 1996; Klimesch et al., 1998; Sauseng et al., 2005; Busch and VanRullen, 2010; Liu et al., 2013; Abiri et al., 2019; Jin et al., 2019).

It is commonly understood that a crucial step in EEG processing is to extract relevant features for the considered application (Xu et al., 2021). Moreover, the study of EEG data, similarly to other neural data, is further complicated by the high degree of cross-subject variability (due to differences in how the information is represented in the brain, e.g., in terms of the representation of stimulus and activity in the brain), and presence of noise (due to changes in machine calibration, spurious participant movements, and environmental conditions) (Rieck et al., 2020).

The goal of this paper is to investigate which type of representations or features of EEG data are the most associated with human attention. We will consider a number of different representations of EEG data (Section 2.2, Supplementary Material Section 2), including both the features obtained from the univariate time series from a single EEG channel (and then concatenated across channels), such as time domain features and recurrence plots, as well as representations obtained directly from the multivariate time series, such as global field power or functional brain networks. These two groups of methods are related to the two key principles that help in understanding brain-behavior relationships: segregation, which assumes that the cerebral cortex can be divided into distinct modules, each with its unique structure and functionality; and integration, which assumes that no brain region functions in isolation but rather requires interactions and information exchange between different regions (Mohamed et al., 2018). Since we aim to deal with the issue of person-to-person variability in the EEG data, we found it particularly interesting to consider some topology-based features. Indeed, persistent homology (PH), the main tool of topological data analysis (TDA, Supplementary Material Section 1) can be made invariant under different type of transformations (such as translation, rescaling, stretching, or even non-affine deformations), and the stability theorems (Cohen-Steiner et al., 2007) imply that the same is true for robustness to noise. Persistent homology has been widely applied in neuroscience: we provide a review of relevant literature in the background on TDA (Supplementary Material Section 1), and in the description of the PH-based pipelines on univariate (Section 2.2.4) and multivariate (Section 2.2.8) time series.

We compare the performance of the different EEG representations on the WithMe data (Section 2.1), obtained from a modified digit span experiment. The performance is evaluated as the Support Vector Machine (SVM) accuracy on the features (Section 2.4). As a baseline, we also include benchmark EEG-specific models which are shown to work well for the WithMe data (Mortier et al., 2023), including a deep learning architecture that learns the best features for the task at hand from the EEG multivariate time series. In order to investigate the cross-subject variability, we consider three different scenarios: the accuracy is evaluated on the model trained on the same participant, on seen or on new participants. The results are summarized in Section 3, and in Section 4 we position them relative to the literature, and discuss the main take-aways and resulting directions for future work.

2 Materials and methods 2.1 WithMe EEG data acquisition

The experiment includes 42 participants EP01-EP42 (20 female and 21 male, with mean age of 23.71 ± 2.69 years, with no visual or hearing difficulties), who have 64 electrodes positioned on their scalp according to the EEG 10 − 10 system (Figure 1, left panel). The EEG data was acquired with the BioSemi ActiveTwo amplifier, together with their caps and gel-based electrodes, and sampled at 2,048 Hz. Each participant is shown 30 sequences of 10 stimuli on a computer screen: 5 Targets (black digit in a circle), and 5 Distractors (dark gray digit in a circle, or an empty circle), with each digit presented with equal probability (for an example sequence, see Table 1). Each of the sequences is shown under four different conditions C1, C2, C3, or C4, in a pseudo-randomized manner, that differ with respect to presence of audio and/or rhythm with no special mention about them made to the participants, in order not to draw their attention to it (Figure 1, right panel). We note that, for conditions C2 and C4 where there is rhythm, each participant is first shown 5 induction stimuli in each sequence to induce the rhythm, but these are ignored in our analysis. Therefore, every participant sees in total 30 × 10 × 4 = 1200 Target or Distractor stimuli. Every stimulus is visible for 200 ms, and the inter-stimulus interval is on average 1.25 s. The task is to remember the Targets, and the participants need to give their oral responses after the complete sequence is presented. The participants do not know that there are always 5 Targets: they are told they will see “5-7 black numbers,” in order to not be able to predict the end of the Target stimuli, but to rather keep focusing until the end of the sequence.

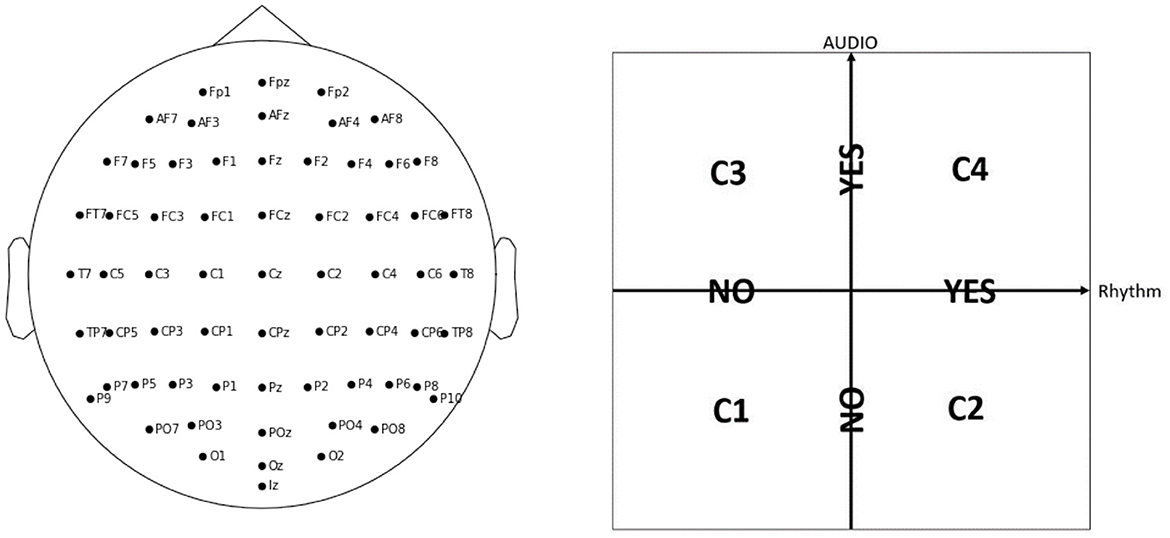
Figure 1. In the WithMe experiment, 64 EEG electrodes are considered, according to the 10–10 system (left panel). Every sequence of numbers is shown to each participant under four different conditions, C1, C2, C3, or C4, which indicate the presence of auditory and/or rhythmic support (right panel).

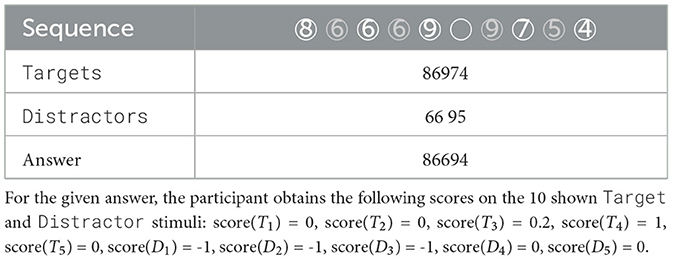
Table 1. An example of a sequence of stimuli shown to each experimental participant on a computer screen, with the digits appearing one by one, Targets in black and Distractors in gray.

The WithMe experiment is a novel working memory paradigm that is somewhat inspired by the digit span, oddball and pip-and-pop tasks. The magical number 7 ± 2 is the average digit span of healthy adults (Miller, 1956), so that a sequence of five digits should be fairly easy to remember for a young adult. The digit span memory task is modified by including Distractors between Target stimuli. In the oddball attention task, a series of repetitive standard stimuli are infrequently interrupted with a rare oddball stimulus that the participant is instructed to focus on. In the WithMe experiment, however, there is an equal number of Target and Distractor stimuli, so there are no oddballs. The pip-and-pop attention paradigm makes the Targets immediately noticeable among the surrounding items (they “pop out”), but the difference between the WithMe Target and Distractor stimuli is very subtle. In summary, the WithMe experimental design complicates the three paradigms, in order to allow to more easily observe the effect of added support on attention. Further details can be found in the first paper that introduces the WithMe experiment, and provides an in-depth analysis of behavioral factors (such as musical education, audiovisual dominance, noise sensitivity, gender, age, etc.) on the influence of audio and/or rhythm on attention for the WithMe data (De Winne et al., 2022).

The data is pre-processed according to standard techniques: the amplitude values are referenced to the average of the both earlobes, bad channels are detected after visual inspection and then interpolated using the spherical spline method (Perrin et al., 1989), notch filter is applied at 50 Hz, and bandpass filter between 0.2 and 100 Hz. The data is then epoched from -0.2 s to 1 s, and a visual inspection of ICA components is performed to remove artifacts. Finally, we downsample the time series with the subsampling period of 50, resulting in 60 time steps, so that each time step corresponds to 1,200 ms/59 = 20.34 ms. In most situations, downsampling the results to 40 or 50 Hz (thus, one time point every 25 or 20 ms) maintains the advantages of downsampling with minimal loss of information (Cohen, 2014). Finally, the EEG amplitude values are cut off within range [−50 μV, 50 μV]. The WithMe dataset can then be seen as a 42 × 1200 × 64 × 60 matrix:

• 60 time steps (within 1.2s),

• 64 EEG channels,

• 1, 200 epochs, i.e., EEG multivariate time series reflecting a single stimulus, across channels,

• 42 participants.

Some examples of the WithMe EEG multivariate time series across 64 electrodes, for a single participant and a single stimulus, are visualized in Figures 5, 8.

2.2 Multivariate time series analysis

In this section, we describe in detail the different approaches to multivariate time series analysis that we will evaluate in the computational experiments. These methods rely on the different types of features, or representations of multivariate time series, that belong to two different groups. Firstly, one can consider the individual univariate time series (for each EEG electrode), and concatenate the information extracted from each of them separately (Sections 2.2.1–2.2.4). Alternatively, we can focus on the relationship between the univariate time series (i.e., relationship between different brain regions), which we summarize in a few different ways (Sections 2.2.5–2.2.10). The latter approaches include the baseline xDAWN-RG model (Congedo et al., 2017), the IEEE Neural Engineering Conference 2015 Brain Computer Interface (BCI) challenge winner, and EEGNet (Lawhern et al., 2018), a benchmark deep learning architecture for EEG signal processing and classification which learns the best representation for the given task, that have both been shown to perform well on the WithMe data (Mortier et al., 2023). A visual summary of all of the different approaches is given in Figure 2.

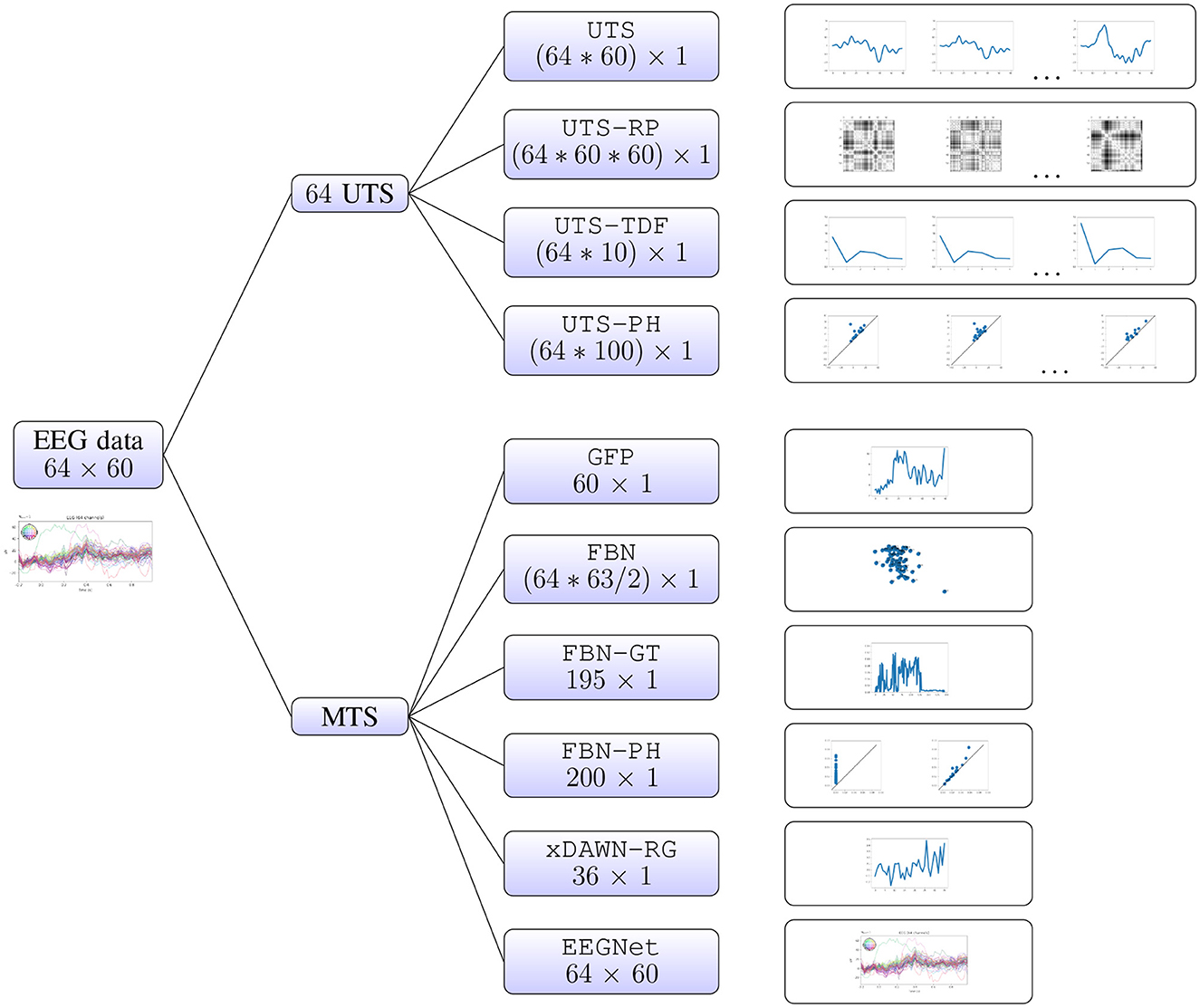
Figure 2. Multivariate time series analysis. A WithMe data observation, an EEG multivariate time series across 64 electrodes and 60 time steps (reflecting the brain signals for some participant and stimulus shown on the screen) can be represented with different types of features. We can consider the 64 univariate time series (UTS) for each EEG electrode, extract features from each of them separately, and concatenate the information (top branches). It is also possible to calculate the features from the multivariate time series (MTS) itself, that rely on the relationship between the 64 EEG channels (bottom branches).

2.2.1 Univariate time series (UTS)

Probably the most straightforward way to transform a multivariate time series into a vector is to concatenate the univariate time series across all features. For instance, a WithMe multivariate time series across 64 electrodes and 60 time steps (matrix of shape 64 × 60) can be represented as a vector of length 3840 = 64*60.

2.2.2 Recurrence plots of univariate time series (UTS-RP)

A recurrence is a time the trajectory returns to a location it has visited before. For a univariate time series, the recurrence plot is a matrix of distances in the signal between every pair of points in time. A WithMe multivariate time series across 64 electrodes and 60 time steps (matrix of shape 64 × 60) can in this way be represented with a vector of length 230400 = 64*60*60, corresponding to the flattened 60 × 60 recurrence plots, concatenated across 64 EEG electrodes. Recurrence plots have been employed in EEG analysis, for example for emotion recognition (Bahari and Janghorbani, 2013), or to differentiate between seizure-free, pre-seizure and seizure states in genetic absence epilepsy rats (Ouyang et al., 2008).

2.2.3 Time-domain features of univariate time series (UTS-TDF)

Instead of looking at the whole univariate time series for each channel (UTS pipeline, Section 2.2.1), we can also only extract some statistics about the time series, such as their maximum, minimum, mean and variance. Next to considering the largest peaks in the time series, we include the peaks from within certain intervals, as these are related to the so-called event-related potentials (ERPs). An ERP is a stereotyped brain response to a specific sensory, cognitive, or motor stimulus. ERP waveforms consist of a series of positive and negative voltage deflections, which are related to a set of underlying components. Most components are referred to by a letter (N/P) indicating polarity (negative/positive), followed by a number indicating either the latency in milliseconds or the component's ordinal position in the waveform:

• N100 or N1: This is the first substantial peak in the univariate time series. It is a negative-going peak typically occurring about 100 ms after a stimulus is presented, but may exhibit a peak anywhere between 80 and 120 ms (280 and 320 ms after the start of our time series, see Section 2.1). We therefore calculate the minimum of the waveform within this range (between time steps t = 13 and t = 16 in our time series).

• P100 or P1: This is a positive extreme occurring about 100 ms after a stimulus is presented, but may exhibit a peak anywhere between 80 and 120 ms. We therefore calculate the maximum of the time series within this range (between time steps t = 13 and t = 16 in our time series).

• P200 or P2: This is the second substantial peak in the time series, which often occurs about 200 ms after the stimulus onset. We calculate it as the maximum of the waveform between 150 and 275 ms, i.e., between time steps t = 17 and t = 24 in our time series.

• P300 or P3: This is the third substantial positive-going peak in the waveform, occurring about 300 ms after a stimulus is presented. We calculate it as the maximum of the waveform between 250 and 500 ms, i.e., between time steps t = 22 and t = 35 in our time series.

A review of EEG/ERP applications can be found in Nidal and Malik (2014). In particular, multiple ERPs were found to be associated with mind-wandering (Jin et al., 2019), or different stages of attention (Abiri et al., 2019). Note that the EEG reflects thousands of simultaneously ongoing brain processes, making it challenging to see the brain response to the event of interest in the EEG recording of a single trial (Blankertz et al., 2011). To see the brain's response to a stimulus, the experimenter commonly conducts many trials and averages the results, causing random brain activity to be averaged out and the relevant waveform to remain (Cohen, 2014). However, in this work we focus on applications that aim to predict the attention from the given EEG time series corresponding to some stimulus, and we therefore extract the given metrics for each EEG epoch. We represent each of the univariate time series with 10 time-domain features: maximum, minimum, mean, variance, skewness, kurtosis (similar to Mohamed et al., 2018) N1, P1, P2, and P3 peaks, and then concatenate the information across EEG electrodes. In this way, a WithMe 64 × 60 multivariate time series is represented with a vector of length 640 = 64 * 10.

2.2.4 Persistent homology of univariate time series (UTS-PH)

The shape of the EEG wave has been shown to contain useful information about the state of the brain (Kannathal et al., 2005). For this reason, we represent EEG time series for each channel with its persistent homology with respect to the lower-star filtration (Supplementary Material Section 1) directly on the signal, i.e., on the function f: → ℝ. Persistent homology with respect to such a filtration measures the relative height of the peaks of the EEG signal, but not their width, so that it is invariant to expansion and contraction in the time axis direction (Supplementary Material Section 1, Figure S2; Supplementary Material Section 1, Figure S4, row 5, columns 2 and 4). Moreover, addition of noise to the signal results in minor changes of PH (Supplementary Material Section 2, Figure S4, row 5, columns 2 and 5). This makes PH an interesting candidate for overcoming individual differences across subjects (Dindin et al., 2020).

A similar pipeline is employed for the epileptic seizure, autism and arrhythmia detection from EEG or ECG in Wang et al. (2015), Wang et al. (2019), Majumder et al. (2020), and Dindin et al. (2020). In this work, we represent the WithMe EEG univariate time series with their 0-dimensional 10 × 10 persistence images (Supplementary Material Section 1), so that an EEG epoch for 64 channels and 60 time steps results in a vector of length 6, 400 = 64 × 10 × 10.

2.2.5 Global field power (GFP)

The representations above (Sections 2.2.1–2.2.4) focus on the features from the univariate time series. However, the interactions between the different time series (i.e., different brain regions reflected by the EEG channels) might contain (more) meaningful information. One of the simplest ways to summarize this relationship between the time series is via the global field power (GFP). GFP is a measure of the scalp field strength and corresponds to the standard deviation of the signal across electrodes at each time point (Skrandies, 1990). Thus, it is a one-dimensional time series capturing the spatial variability of the signal across sensor locations. The WithMe 64 × 60 multivariate time series is thus represented as a vector of length 60. GFP has found applications in studies of perceptual, attentional, cognitive and drug-related aspects of information processing (Michel et al., 1993).

2.2.6 Functional brain network (FBN)

From a multivariate time series, one can construct a graph or network, with vertices or nodes which reflect the different univariate time series, and the edges which describe some relationship between them. In the context of (WithMe) EEG multivariate time series, the nodes correspond to the different EEG electrodes or brain regions, and the weights of the edges correspond to some measure of connectivity between them, with the resulting graph commonly referred to as a functional brain network (Stolz et al., 2018). These functional brain networks provide a new understanding of the characteristics of the brain, since different cognitive or perceptual tasks require a coordinated flow of information within networks of functionally specialized brain areas (Bastos and Schoffelen, 2016).

Indeed, changes in the topology of EEG functional brain networks appear to accompany a series of neurological and psychiatric disorders, such as stroke damage (de Vico Fallani et al., 2009), schizophrenia (Jalili and Knyazeva, 2011b; Micheloyannis et al., 2006), amyotrophic lateral sclerosis (ALS; Fraschini et al., 2016) or Alzheimer's (Stam et al., 2007; Jalili, 2016; Yu et al., 2016), and can therefore be used as diagnostic markers for these conditions (Stolz, 2014). Moreover, several studies have suggested that EEG interregional correlations are associated with conscious cognitive processing and active perception (de Vico Fallani et al., 2009; Tóth et al., 2019).

The correlation between time series (i.e., connectivity between brain regions) can be calculated in many different ways, such as cross-correlation, coherence, and synchronization likelihood. In our computational experiment, we will consider the common Pearson product-moment correlation coefficients (Jalili and Knyazeva, 2011a). The distance dij between the two univariate time series i and j is then calculated as dij = 1−pij, where pij is the Pearson correlation. As input for this FBN pipeline, we will consider the distance matrix itself, above the diagonal and flattened into a vector, similarly to Rathore et al. (2019). The WithMe 64 × 60 multivariate time series thus results in a 64 × 64 distance matrix, that is then flattened into a vector of length 2, 016 = 63*64/2.

2.2.7 Graph theory of functional brain networks (FBN-GT)

Instead of feeding the complete correlation or distance matrix to a machine learning algorithm (FBN pipeline, Section 2.2.6), it is common to analyze such a matrix (or functional brain network in the neuroscience context) using graph theory. Typically, the weighted graph, i.e., the correlation or distance matrix is thresholded at a prespecified level to produce the binary adjacency matrix that only indicates if a connection between vertices exists (Lee et al., 2011). Then, the corresponding graph topology of the binary matrix can be characterized by calculating the graph metrics of interest that characterize the functional integration and segregation.

Indeed, significant differences across some graph theory metrics have been found between EEG brain networks for control subjects and patients of a range of neurological and psychiatric disorders (Bullmore and Sporns, 2009; Fraschini et al., 2016) (such as stroke, multiple sclerosis, Parkinson's, epilepsy or depression). Moreover, in the healthy brain, individual variability in cognitive functions, learning a new task, or the predisposition to learn have been correlated with specific patterns of network connectivity (Khalid et al., 2014). In our computational experiments, we consider the commonly used assortativity degree, average path length, edge connectivity, and for each vertex, its degree, betweenness, and eccentricity, that provide insights into how different brain regions communicate and interact:

• Assortativity measures the tendency of vertices to connect with other vertices with a similar degree (number of adjacent edges, see below). High assortativity means that highly connected vertices (hubs) tend to be connected with other hubs. In the brain, this can indicate a resilient and efficient network because hub-to-hub connectivity is critical for global communication. A low assortativity may imply a more vulnerable network, where the failure of a single hub can more easily disrupt information flow.

• Average path length is self-explanatory, it is the average shortest path length between all vertex pairs. Shorter path lengths indicate more efficient global communication across the network. In the brain, a network with a shorter average path length facilitates fast information flow across distant brain regions, which is critical for efficient integration of information between different functional systems.

• Edge connectivity between two vertices is the number of edges that have to be removed in order to disconnect the two vertices into two separate components, or equivalently, to eliminate all paths between them. The edge connectivity of a graph (or group adhesion) is the minimum of the edge connectivity of every pair of vertices in the graph. Multiple connections between regions create redundant routes, which are important for ensuring reliable communication and cognitive flexibility. High edge connectivity thus implies that brain networks can resist damage, maintaining communication pathways and ensuring stable function.

• The degree of a vertex is its most basic structural property, the number of edges that are connected to that vertex, measuring how many direct connections a vertex has with other vertices in the graph. Vertices with a high degree are considered hubs and may play a key role in information integration and transmission across the brain. In functional brain networks, a region with a high degree is likely involved in widespread functional connectivity and might be important for global network communication.

• The betweenness centrality of a vertex is the number of shortest paths going through it. Vertices with high betweenness centrality are key to information flow across the network because they act as critical “bridges” between different brain regions or modules. Such verticess may be vulnerable to damage, as their failure could disrupt communication between distant parts of the brain.

• Eccentricity of a vertex is the shortest path distance from the farthest other vertex in the graph. Eccentricity provides information about the relative position of a brain region in the broader network and its role in global communication. High-eccentricity vertices are more isolated or peripheral, often supporting localized, specialized processing within functional modules, while low-eccentricity vertices integrate information from various parts of the brain.

To obtain the graph adjacency matrix, the normalized distance matrix (see FBN pipeline in Section 2.2.6) is thresholded at 0.1. For a WithMe EEG multivariate time series across 64 channels, i.e., a 64 × 64 functional brain network (distance matrix), this results in a vector of length 195 = 1+1+1+64*(1+1+1).

2.2.8 Persistent homology of the functional brain network (FBN-PH)

Studying the correlations using graph theory or network science (FBN-GT pipeline, Section 2.2.7) suffers from methodological problems. Firstly, finding a proper threshold is one of the crucial issues, since the graph structure drastically changes depending on how to threshold a connectivity matrix. For example, most graph characteristics depend on the number of edges in the graph, and the estimated graph topology is therefore biased by the choice of the threshold. This hampers a meaningful comparison of graph topology between individuals or groups. Some of the proposed thresholding methods, such as the multiple comparisons correction and the sparsity control, assume that the strongly connected edges are only important; however, it is suggested that the weakly connected edges may also have discriminative information between networks (Bassett et al., 2012; Lee et al., 2012). The choice of threshold has a major influence on the resulting graph (Gracia-Tabuenca et al., 2020) and inevitably leads to a loss of information. Determining the threshold can be based on the statistical significance by the false discovery rate or by fixing the graph metrics such as number of vertices and edges. However, these methods are fairly ad-hoc and everyone seem to use different thresholding techniques. This arbitrariness is demonstrated in Lee et al. (2011, Figure 1), where it is shown that the number of edges, the number of connected components and smallworldness of a brain network substantially change depending on the threshold: by varying the threshold, the topology changed to random-like, small-world and clustered network. In addition, it was shown that the clustering coefficient, modularity, efficiency, efficiency-cost show and assortativity of a brain network change greatly across different thresholds (reflected by the network cost, i.e., the total number of edges; Joudaki et al., 2012, Figures 3–7), and the same was shown to be true for efficiency, clustering coefficient, small-worldness, modularity, vertex and edge betweenness centrality, variance of vertex degrees, assortativity, and synchronizability in Jalili and Knyazeva (2011a, Figures 5–8). Ideally, graphs should be characterized across a broad range of thresholds (Rubinov and Sporns, 2010).

Moreover, in many real systems, dyadic relationships between pairs of vertices fail to accurately capture the rich nature of the system's organization, e.g., cognitive functions appear to be performed by a distributed set of brain regions and their interactions (Giusti et al., 2016). Furthermore, another drawback of the common graph theory approaches is that they require 2-dimensional embedding of structures that might otherwise be of higher dimension (Bendich et al., 2016).

Persistent homology (PH) of a graph goes beyond graph-theoretic analysis by describing the architecture of a graph in more flexible ways, that investigates the persistence of relationships between graph vertices across multiple scales (Anderson et al., 2018). Instead of trying to determine one fixed optimal threshold, PH allows us to look at the topological changes of graphs while increasing the threshold continuously. Persistent homology represents the weighted graph with a finite number of nested binary graphs over every possible threshold. In contrast to standard methods of graph or network analysis, PH also encodes higher order connections and thus allows to go beyond pairwise connections; this is helpful for gaining global understanding of low-dimensional structures in graphs (Stolz et al., 2018). Indeed, experimental results in Guo et al. (2022) show that compared with the existing methods, PH can extract the topological features of brain networks more accurately and improves the accuracy of diagnostic and classification.

The first papers that deal with PH of brain networks (Lee et al., 2011, 2012) demonstrate differences between the local connectivity structures in functional brain networks for attention deficit hyperactivity disorder (ADHD) and autism spectrum disorder (ASD), and later, in a depressed brain (Khalid et al., 2014; Yoo et al., 2014). Furthermore, PH metrics have been employed to investigate how the topological architecture of brain networks is related to cognitive function, behavior and personality (Anderson et al., 2018; Liu et al., 2021; Yoo et al., 2016). In this paper, we employ PH with respect to the rank filtration (Section A.1) on the functional brain networks. This is useful in neuroscience applications, where correlations cannot be assumed to give a precise definition of the distances between graph nodes, and the PH defined in such a way remains unchanged under nonlinear monotonic transformations of the distances (see Supplementary Material Section 1, Figure S3). More precisely, we concatenate both the 0- and 1-dimensional 10 × 10 persistence images (that respectively reflect the connected components or clusters, and loops) for each graph, so that a WithMe 64 × 64 functional brain network is represented with a vector of length 200 = 10*10+10*10.

2.2.9 xDAWN-RG (xDAWN-RG)

As one of the baselines, we consider xDAWN-RG, one of the benchmark techniques for classification of multivariate bio-signals, like EEG, MEG, or EMG. xDAWN-RG was the winner of the IEEE Neural Engineering Conference Brain Computer Interface (BCI) challenge (Mattout et al., 2014), whose goal was to detect errors during a spelling task, given subject's EEG data. It consists of applying xDAWN spatial filters (Rivet et al., 2009), calculating covariance matrix between the EEG channels to encode their statistical dependencies (Barachant and Congedo, 2014; Congedo et al., 2013), selecting the channels via Riemannian Geometry (RG) (Barachant and Bonnet, 2011), and projecting the reduced covariance matrices in the tangent space (Barachant et al., 2011, 2013). A WithMe 64 × 60 multivariate time series is transformed into a 8 × 8 covariance matrix, which is then projected into a vector of length 36 = (8+1)*8/2.

2.2.10 EEGNet (EEGNet)

As the main baseline, we consider EEGNet (Lawhern et al., 2018), a benchmark deep learning architecture for EEG signal processing and classification, with default parameter values. EEGNet is a convolutional neural network (CNN) that learns the best representation for the given task directly from the multivariate time series, with each data observation corresponding to the matrix of univariate time series across channels. Therefore, the raw WithMe 64 × 60 multivariate time series is fed directly to the model.

2.3 Attention score

The focus of this paper and the WithMe data acquisition (Section 2.1) is attention recognition. Remember that each experimental participant is shown 30 sequences of 10 Target or Distractor numbers on the screen, and is instructed to list the Targets in the correct order of appearance. We are thus interested to what degree the different pipelines (Section 2.2) can predict how well a participant was able to remember the Targets and ignore the Distractors from the EEG data. To do so, we define a simple scoring function, which reflects the digit recall accuracy, i.e., how well a participant was paying attention to the given stimulus.

Note firstly that the attention performance is not always conclusive, since the Targets and Distractors in a sequence are not necessarily unique: e.g., if a sequence contains digit 5 both as a Target and as a Distractor, and a participant reports 5, we do not know if the participant correctly remembered the target, or did not properly ignore the distractor. We assign such stimuli a value of -1.

We define the scoring function for the remaining, well-behaved stimuli to take values in [0, 1]. The score of 0 indicates perfect performance: Target stimulus is given in the participant's answer in the correct position, or the Distractor stimulus was properly ignored. On the other extreme, the score of 1 means that the participant did not remember the Target, or has listed the Distractor in their answer. The scores of 0.2, 0.4, 0.6, or 0.8, that are only possible for the Targets, aim to capture that a participant remembered the Target, but at the wrong position; the value of the score indicates how wrong is the provided answer. Note, however, that e.g., a score of 0.2 for some Target stimulus does not necessarily imply that the subject was not paying “perfect” attention, since it might rather be that they were not attentive during a previous Target that they thus did not include in their answer. Since a stimulus might appear multiple times in a sequence, note also that the scoring function does not necessarily always correctly reflect the attention, and a participant might simply “get lucky” and report the number correctly.

Therefore, our simple scoring function is defined as follows:

score(T)= is too small for a score prediction task (left plot), so that this data is also removed. In this way, score prediction amounts to classification between score = 0 (attentive) and score = 1 (inattentive) stimuli or EEG epochs.

2.4 Experimental set-up

The classification is done with a linear SVM on the features obtained in the pipelines, except for EEGNet that classifies the multivariate time series directly. According to a recent review (Lotte et al., 2018), due to its good performance, SVM is among the most popular types of classification algorithms for EEG. Moreover, we also want to evaluate to what extent are the different pipelines able to deal with the person-to-person variability, as this is an important challenge of EEG data (Section 1). To this end, we consider three different experimental scenarios, that differ in the train and test data used for classification:

• Classification per participant: We start with the simplest scenario, when the model is trained on 70% of data (randomly chosen EEG epochs) for a single participant, and the test data corresponds to the remaining 30% of multivariate time series for that same participant.

• Classification on seen participants: Next, we train the models on 70% of randomly chosen multivariate time series, and test on the remaining data. In this case, the train and test data consists of all (and therefore, the same) participants.

• Classification on new participants: Finally, we train the models on all the EEG data from 70% of the experimental participants, and test on the complete data for the remaining 30% participants. Here, the test data consists of new participants compared to the train data.

For each of the three scenarios, we consider three different splits between train and test data, which are the same across different pipelines. The drop in accuracy from the test data consisting of seen and new participants (the last two scenarios above) can give an idea of how well a pipeline is able to avoid the issue of cross-subject variability. Note that the size of data differs greatly between the first, and second and third experimental scenario, since the former is limited to the EEG data from a single participant. The data size for each experiment is explicitly mentioned in Section 3.

Finally, note that the UTS-RP, UTS-TDF and UTS-PH pipelines that extract features from the univariate time series yield a large number of features (relative to the number of data observations, e.g., 230400 UTS-RP features for 1200 data samples in the first experimental scenario where we focus on an individual subject). To reduce the computational efforts, we limit these pipelines to the features from the 10 most important EEG channels, identified by the UTS pipeline: we take these to be the EEG channels with the largest values of the linear SVM coefficients trained on the complete data. Removal of noisy of irrelevant channels can also make the model less prone to overfitting (Montoya-Mart́ınez et al., 2019), but we did not observe important differences when using only a subset of features.

For some of the classification problems, the data is very unbalanced: for instance, the number of EEG epochs with score=1 is quite small in comparison with score = 0 (Figure 3), so that even a random guess yields a very high accuracy. For this reason, we consider a balanced accuracy, which is calculated as the average between the true positive rate or recall TPTP+FN, and the true negative rate TNTN+FP, where TP, TN, FP and FN are respectively the number of true positives, true negatives, false positives and false negatives. If the data is well-balanced, the accuracy and balanced accuracy tend to converge to the same value. We opt for an adjusted classification accuracy in order to allow for a fair comparison across participants (which would not be the case if we oversampled some epochs for some participants), simultaneously avoiding data loss due to undersampling.

3 Results 3.1 Score prediction

The goal of this subsection is to evaluate to what extent can EEG signals predict the attention score (Section 2.3) that reflects how well a person has remembered the given Target, or ignored the given Distractor stimulus, shown on the computer screen. We thus perform the classification separately for Target and Distractor stimuli, as the score might reflect different types of attention. We limit the data to EEG multivariate series with score = 0 (attentive) and score = 1 (inattentive), in order to focus only on the stimuli for which we are fairly confident whether a participant was paying attention. Indeed, as we discuss in Section 2.3, the data samples with score=-1 are inconclusive, and score ∈ might often be misleading. Moreover, there is only a limited number of stimuli with a score of 0.2, 0.4, 0.6, or 0.8 (Figure 3, left panel) so that any classifier would struggle to learn to recognize such signals. This results in a somewhat different number of appropriate EEG epochs across participants (Figure 3, right panel). To make the comparisons across participants fair, we select the same number of Target and Distractor EEG epochs for each participant. Participant EP09 has the minimum number of Target epochs with a conclusive score (303), whereas participant EP17 has the least conclusive Distractor epochs (357). We therefore randomly choose 303 Target and 357 Distractor epochs for every participant. Note that, since we are evaluating the balanced classification accuracy (Section 2.4), we do not further enforce the same number of Target and Distractor epochs, in order to avoid further data loss.

Figure 4 shows the balanced accuracy for score = 0 vs. score = 1 classification for the different pipelines (Section 2.2), for the three different experimental scenarios, i.e., train and test data (Section 2.4). In general, most of the pipelines perform extremely poorly, and are not much better than a random guess with an accuracy of 0.5.

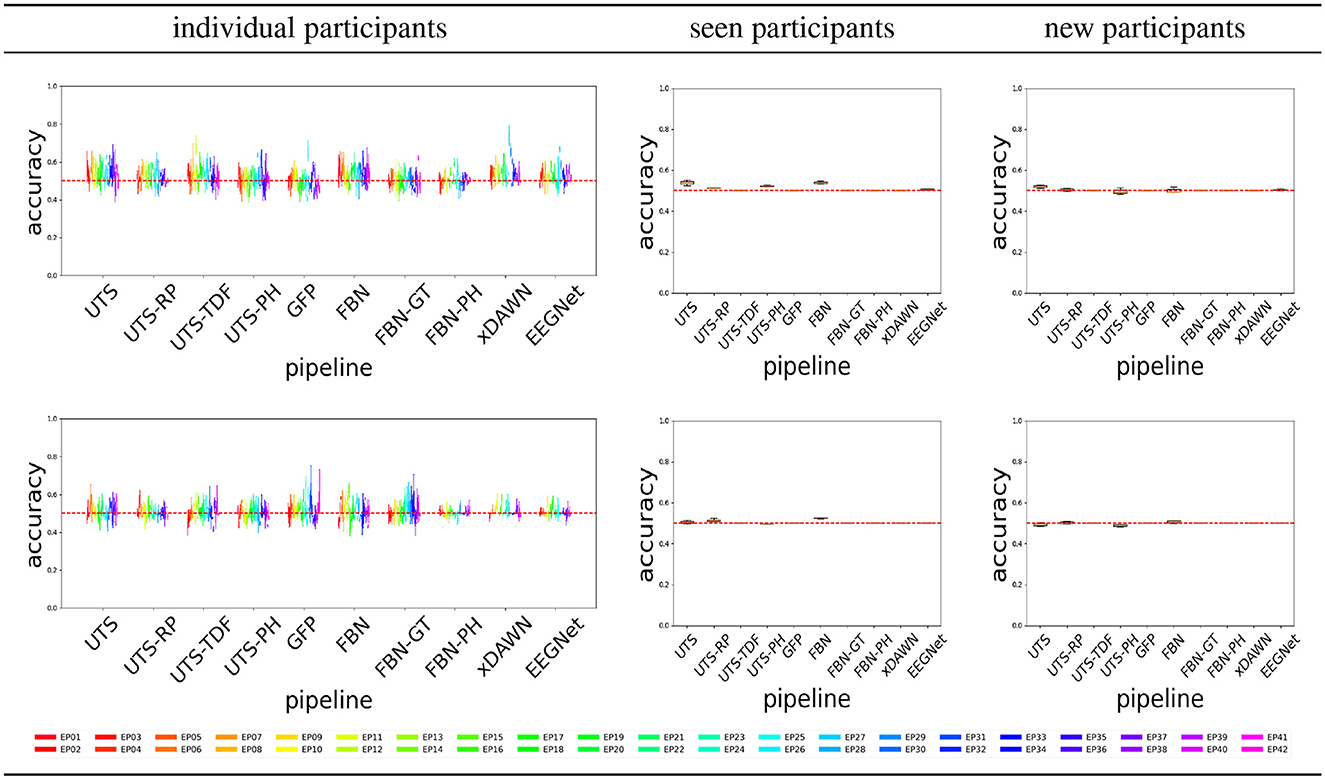
Figure 4. Score 0 (attentive) vs. 1 (inattentive) classification accuracy across the pipelines, for the Target (top row) and Distractor (bottom row) stimuli.

3.2 Classification between Target and Distractor stimuli

In this section, we perform the classification between Target and Distractor stimuli, since P300 ERP is expected to be observed when subjects see a Target stimulus, and the amplitude of the P300 has shown to be proportional to the amount of attentional resources engaged in processing a given stimulus (Gray et al., 2004). Indeed, Mortier et al. (2023, Figure 2) shows that the evoked response for an example WithMe participant exhibits a clear positive voltage deflection around 300ms post-stimulus in the parietal-occipital electrodes. This can also be observed in Figure 5, which shows an example of EEG multivariate time series for a participant, for the different type of stimuli. Classification between Targets and Distractors investigates whether the brain responds differently to the two different stimulus types, which is thus informative of attention, but does not depend on the particular choice of the attention score.

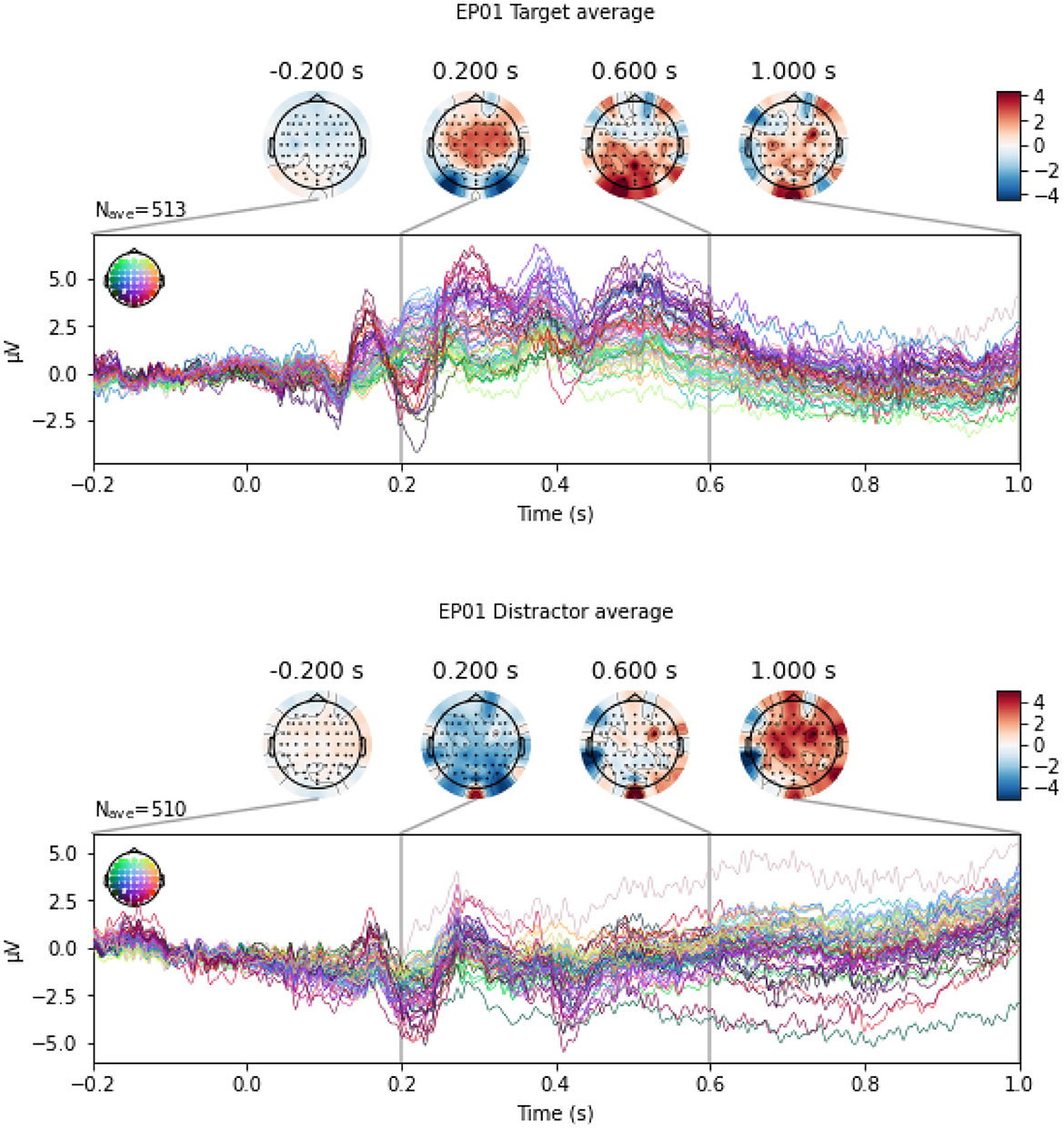
Figure 5. An example of EEG signals across 64 EEG electrodes for participant EP01, averaged across Target (top panel) and Distractor (bottom panel) stimulus.

Remember that the WithMe experiment is performed under four experimental conditions C1-C4, that indicate the presence of rhythmic or auditory support (Section 2.1). Whenever present, the rhythm and audio accompany the Targets only (and not the Distractors), and in order to ensure that the classification above is a differentiation between the Target and Distractor stimuli rather than a detection of rhythm and auditory support, we perform the classification separately under each condition. Note, moreover, that the subjects do not always correctly identify the Target or Distractor stimulus, so that their EEG signals do not necessarily exhibit a behavior that might be representative of the different type of stimuli. To avoid this issue, we limit the classification only to stimuli that were perfectly remembered or ignored (score = 0). Restricting the data in such a way results in somewhat different number of appropriate EEG epochs across participant, and we randomly select the minimum number of respectively 109, 84, 87, and 106 EEG epochs for conditions C1-C4.

Figure 6 shows that a number of pipelines achieve a good classification accuracy of 75% or more. What is probably the most surprising is that the simplest pipeline UTS (Section 2.2.1), where the univariate time series across 64 EEG channels are simply concatenated into a large vector, obtains a very good performance, at times even outperforming the benchmark xDAWN-RG and deep learning EEGNet methods. Overall, in this case, the pipelines that extract and then concatenate the features from each of the univariate time series separately (UTS, UTS-RP, UTS-TDF, UTS-PH) outperform the pipelines that focus on the relationship between the time series across EEG channels (GFP, FBN, FBN-GT, and FBN-PH).

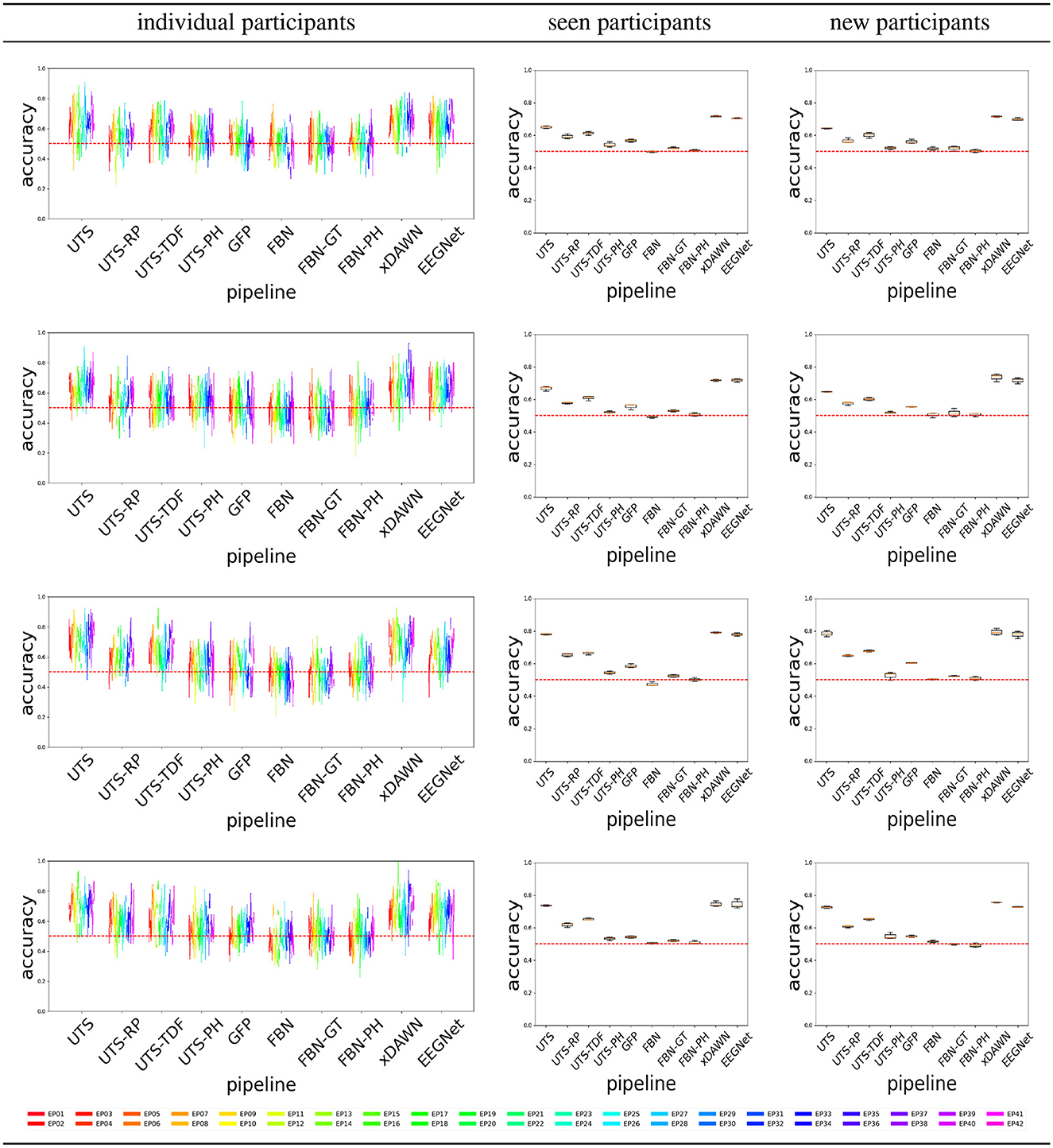
Figure 6. Target vs. Distractor classification accuracy across the pipelines, for conditions C1-C4 shown respectively from (top to bottom row).

3.3 Classification between conditions C1, C2, C3, and C4

Next to attention recognition, one of the goals of the WithMe experiment (Section 2.1) is to investigate to what extent can rhythmic and/or auditory clues (Figure 1, right panel) improve attention. There is no significant difference among the distribution of attention scores, or scores averaged across participants, for the four experimental conditions C1-C4. This is because the perception of the auditory and/or rhythmic support turns out to be a very individual experience, improving the task performance for some, and causing distraction for other participants. We therefore rather visualize the attention score separately for each participant (Figure 7).

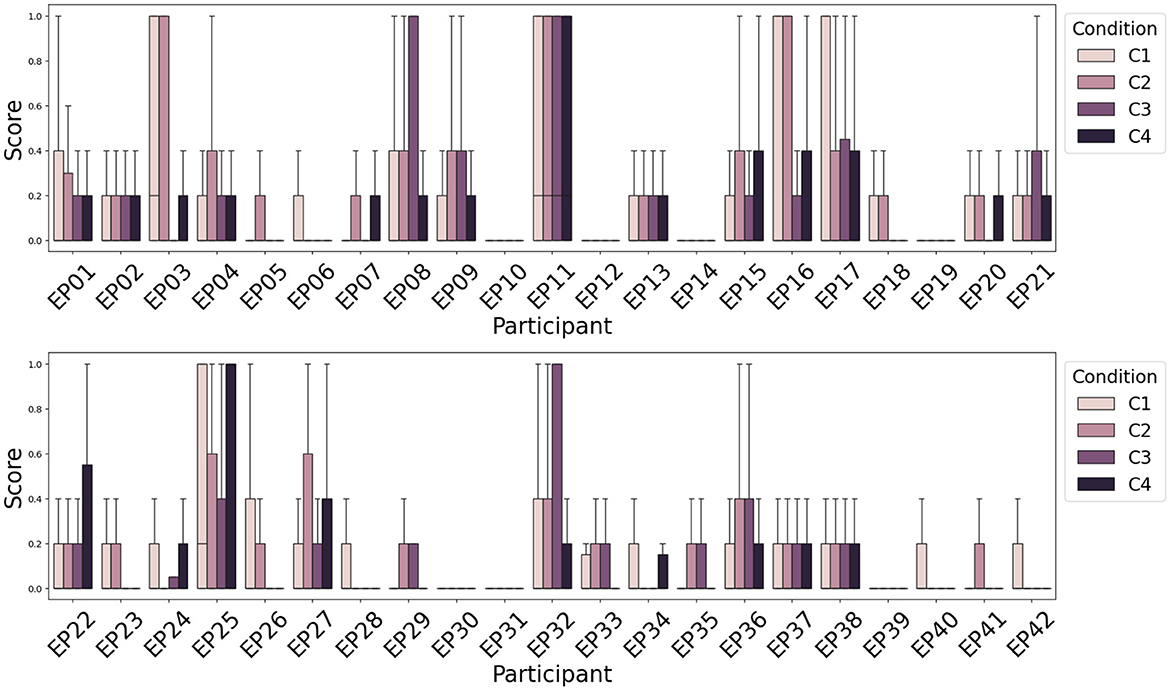
Figure 7. Average attention scores (lower is better) across participants and experimental conditions indicate that the influence of rhythmic and/or auditory support on the attention score is different across participants. Rhythm (C2) deteriorates the performance more often than improving attention. Auditory support (C3), however, improves the attention score for the majority of participants.

Figure 7 shows that for the majority of the participants, the presence of rhythm alone (C2) does not improve their attention score (Section 2.3) during the modified digit span task, although there are some differences across subjects. However, the presence of auditory support (C3) commonly helps to achieve a better score, that is rarely improved further with the additional rhythmic support (audio and rhythm together, C4). This is consistent with earlier findings on the WithMe data (De Winne et al., 2022), for three different scoring functions that look into the performances across complete sequences of digits shown on the screen (rather than for each of the 10 individual stimuli in a sequence).

In this section, we classify between the experimental conditions C1, C2, C3, and C4, to assess to what extent the EEG signals differ in the presence of rhythm and/or audio. An example of an EEG multivariate time series for a participant, across different conditions, is shown in Figure 8.