1 Introduction

Spiking neural network (SNN) is considered the third generation of artificial neural networks (Maass, 1997) for its biological plausibility of event-driven characteristics. It has also received extensive attention in the computation area of neuromorphic hardware (Davies et al., 2018), exhibiting a remarked lower computational cost on various machine learning tasks, including but not limited to, visual classification (Zhou et al., 2023), temporal auditory recognition (Wang et al., 2023), and reinforcement learning (Tang et al., 2021). The progress in SNN is contributed initially by some key computational modules inspired by the biological brain, for example the receptive-field-like convolutional circuits, self-organized plasticity propagation (Zhang et al., 2021), and other multi-scale inspiration from the single neuron or synapse to the network or cognitive functions. Simultaneously, the SNN also learns from the artificial neural network (ANN) by borrowing some mathematical optimization algorithms, for example the approximate gradients in backpropagation (BP), various types of loss definitions, and regression configurations.

Even though various advanced architectures have been proposed and contributed ANN to a powerful framework, the efforts to promote its training speed and computational consumption have never been stopped. As the well-known transformer for example, it contains a rich information representation formed by multi-head self-attention, which calculates Query, Key, and Value from the inputs to connect each token in a sequence with every other token. Although having achieved rapid and widespread application, the O(N2) complexity (with N representing the sequence length) results in a huge training cost in transformer that can not be neglected. Many works have tried to solve this problem, including but not limited to, replacing self-attention with unparameterized transform formats, for example, using Fourier transform (FNet) (Lee-Thorp et al., 2021) or Gaussian transform (Gaussian attention) (You et al., 2020). Another attempt is to integrate some key features of ANNs and SNNs to exhibit their advantages, such as the higher accuracy performance in ANNs and the lower computational cost in SNNs.

The spikformer (Zhou et al., 2023) explores self-attention in SNN for more advanced deep learning in visual recognition. It introduces a spike-form self-attention called spiking self-attention (SSA). In SSA, the floating Query, Key, and Value signals are sent to leaky-integrated and fire (LIF) neurons to generate spike sequences that only contain binary and sparse 0 and 1 vision information, which results in non-negativeness spiking attention map. This special map doesn't require the complex softmax operation anymore for further normalization, which means a lower computational consumption is needed compared to that in vanilla self-attention. However, even though many efforts have been made, it seems that the SSA still exhibits an O(N2) complexity, for which further refinement is necessary. Given binary and sparse spikes for information representation, we here question whether it is still necessary to retain the original complex structure of Self-Attention in spikformer. Here, we give a hypothesis that although self-attention with learning parameters has been generally considered more flexible, it is still not suitable in the spike stream context, since the correlation between sparse spike trains is too weak to form closed similarity. In the field of image processing, Fourier and wavelet transforms have achieved remarkable success in tasks such as image denoising (Tian et al., 2023), edge detection (You et al., 2023), and image compression (Zhang et al., 2020). Fourier transform specializes in global frequency analysis, while Wavelet transform adds multi-resolution capabilities for both global and local feature capture. These techniques not only offer indispensable tools for feature extraction, enabling precise and efficient analysis, but also form a solid theoretical foundation for deep learning models. Hence, an intuitive approach is to convert these sparse spike trains in spatial domains to the equivalent frequency domains with the help of Fourier or wavelet transformation.

Here we propose a new hypothesis: Just like the Fourier transform, self-attention can also be thought of as using a set of basis frequency functions for information representation. The main difference between these two methods is that the Fourier transform uses fixed triangular basis functions to transform signals into the frequency domain, while on the contrary, the self-attention calculates higher-order signal representation from compositions of the input to produce more complex basis functions (Query×Key). This understanding may explain why FNet (Lee-Thorp et al., 2021) performs well, since fixed basis functions may also work in some cases by offering structured prior information. Following this perspective, an intuitive plan is to integrate all these key features together, toward a reduced computational cost and accelerated running speed, including unparameterized transforms (e.g., Fourier transform and wavelet transform), and spike-form sparse representation. Our main contributions can be summarized as follows:

• We propose a key hypothesis that the self-attention in transformer works by using a set of basis functions to transform information from Query, Key, and Value sequences, which is very similar to the Fourier transform. Hence, after jointly considering the shortcomings of spikformer, we replaced SSA with spike-form Fourier transform and wavelet transform. Mathematical analysis indicates a reduced time complexity from O(Nd2) or O(N2d), to O(NlogN) or O(DlogD)+O(NlogN), under the same accuracy performance.

• The results validate that our method achieves superior accuracy on event-based video datasets (improved by 0.3%–1.2%) and comparable performance on spatial image datasets, compared to spikformer with SSA. Furthermore, it exhibits significantly enhanced computational efficiency, reducing memory usage by 4%–26%, reducing theoretical energy consumption by 20%–25%, and achieving ~9%–51% and 19%–70% improvements in training and inference speeds, respectively.

• We further analyze the orthogonality of self-attention as a set of basis functions. We find during training that the orthogonality is continuously decreasing, which inspires us to use combined different wavelet bases with non-linear, learnable parameters as coefficients to form structured non-orthogonal basis functions. In the second round of experiments, the experiments show even better accuracy performance on event-based video datasets (improved by 0.4%–1.5% compared to spikformer).

2 Related studies 2.1 Vision transformers

The vanilla transformer architecture, initially designed for natural language processing (Vaswani et al., 2017), has demonstrated remarkable success in various other computer-vision tasks, including image classification (Dosovitskiy et al., 2020), semantic segmentation (Wang et al., 2021), object detection (Carion et al., 2020), and low-level image processing (Chen et al., 2021). The critical component that contributes to the success of the transformer is the self-attention mechanism. In Vision transformer (ViT), self-attention can capture global dependencies between image patches and generate meaningful representations by weighting the features of these patches, using the dot-product operation between Query and Key, followed by the softmax normalization (Katharopoulos et al., 2020). The structure of ViT also fits for conventional SNNs, offering potential transformer-type architectures for achieving higher accuracy performance.

2.2 Spiking neural networks

In contrast to traditional ANNs that employ continuous floating-point values to convey information, SNNs utilize discrete spike sequences for communication, offering a promising energy-efficient and biologically plausible alternative for computation. The critical components of SNNs encompass spiking neuron models, optimization algorithms, and network architectures. Spiking neurons serve as the fundamental non-linear spatial and temporal information processing units in SNNs, responsible for receiving from continuous inputs and converting them to spike sequences. Leaky Integrate-and-Fire (LIF) (Dayan and Abbott, 2005), PLIF (Fang et al., 2021a), Izhikevich (Izhikevich et al., 2004) neurons are commonly used dynamic neuron models in SNNs for their efficiency and simplicity. There are primarily two optimization algorithms employed in deep SNNs: ANN-to-SNN conversion and direct training. In ANN-to-SNN conversion (Rueckauer et al., 2017), a high-performance pre-trained ANN is converted into an SNN by replacing rectified linear unit (ReLU) activation functions with spiking neurons. However, the converted SNN requires significant time steps to accurately approximate the ReLU activation, leading to substantial latency (Han et al., 2020). In direct training, SNNs are unfolded over discrete simulation time steps and trained using backpropagation through time (Shrestha and Orchard, 2018). Since the event-triggered mechanism in spiking neurons is non-differentiable, surrogate gradients are employed to approximate the non-differentiable parts during backpropagation by using some predefined gradient values to replace infinite gradients (Lee et al., 2020).

With the advancements in ANNs, SNNs have improved their performance by incorporating advanced architectures from ANNs. These architectures include spiking recurrent neural networks (Lotfi Rezaabad and Vishwanath, 2020), ResNet-like SNNs (Hu et al., 2021), and spiking graph neural networks (Xu et al., 2021). Recently, exploring transformer in the context of SNNs has received a lot of attention. For example, temporal attention has been proposed to reduce redundant simulation time steps (Yao et al., 2021). Additionally, an ANN-SNN conversion transformer has been introduced, but it still retains vanilla self-attention that does not align with the inherent properties of SNNs (Mueller et al., 2021). Furthermore, spikformer (Zhou et al., 2023) investigates the feasibility of implementing self-attention and transformer in SNNs using a direct training manner.

In this article, we argue that the artificial transformer can be well integrated into SNNs for higher performance, while at the same time, the utilization of SSA in spiking transformer (spikformer) can be further replaced by a special module based on Fourier transform or wavelet transform, which to some extent, indicating an alternative more efficient effort to achieve fast, efficient computation without affecting the accuracy.

3 Background 3.1 Spiking neuron model

The spiking neuron serves as the fundamental unit in SNNs. It receives the current sequence and accumulates membrane potential, which is subsequently compared to a threshold to determine whether a spike should be generated. In this article, we consistently employ LIF at all spiking neuron layers.

The dynamic model of the LIF neuron is described as follows:

H[t]=V[t-1]+1τ(C[t]-(V[t-1]-Vreset)),    (1) S[t]=G(H[t]-Vth),    (2) V[t]=H[t](1-S[t])+VresetS[t],    (3)

where τ represents the membrane time constant, and C[t] denotes the input current at time step t. When the membrane potential H[t] exceeds the firing threshold Vth, the spiking neuron generates a spike S[t]. The Heaviside step function G(v) is defined as 1 when v ≥ 0 and 0 otherwise. The membrane potential V[t] will transition to the reset potential Vreset if there is a spike event, or otherwise it remains unchanged as H[t].

3.2 Spiking self-attention

The spikformer utilizes the SSA as its primary module for extracting sparse visual features and mixing spike sequences. Given input spike sequences denoted as X ∈ ℝT×N×D, where T, N, and D represent the time steps, sequence length, and feature dimension, respectively, SSA incorporates three key components: Query (Q), Key (K), and Value (V). These components are initially obtained by applying learnable matrices WQ,WK,WV∈ℝD×D to X. Subsequently, they are transformed into spike sequences through spiking neuron layers, formulated as:

Q=SN(BN(XWQ)),K=SN(BN(XWK)),V=SN(BN(XWV)),    (4)

where SN denotes the Spiking Neuron Layer, BN denotes batch normalization and Q, K, V ∈ ℝT×N×D. Inspired by vanilla self-attention (Vaswani et al., 2017), SSA adds a scaling factor s to control the large value of the matrix multiplication result, defined as:

SSA(Q,K,V)=SN(Q KT V*s),X′=SN(BN(Dense(SSA(Q,K,V)))),    (5)

where X′ ∈ ℝT×N×D are the updated spike sequences. It should be noted that SSA operates independently at each time step. In practice, T represents an independent dimension for the SN layer. In other layers, it is merged with the batch size. Based on Equation 4, the spike sequences Q and K produced by the SN layers SNQ and SNK, respectively, naturally have non-negative values (0 or 1). Consequently, the resulting attention map is also non-negative. Therefore, according to Equation 5, there is no need for softmax normalization to ensure the non-negativity of the attention map, and direct multiplication of Q, K, and V can be performed. This approach significantly improves computational efficiency compared to vanilla self-attention.

However, it is essential to note that SSA remains an operation with a computational complexity of O(N2). Although SSA can be decomposed with an O(N) attention scaling, this complexity hides large constants, causing limited scalability in practical applications. For a more detailed analysis, refer to time complexity analysis of FW vs. SSA section. Within the spike-form frameworks, we are firmly of the view that SSA is not essential, and there exist simpler sequence mixing mechanisms that can efficiently extract sparse visual features as alternatives.

3.3 Fourier transform

The Fourier transform (FT) decomposes a function into its constituent frequencies. For the input spike features x ∈ ℝN×D at a specific time step in X, we utilize the FT to transform information from different dimensions, including 1D-FT and 2D-FT.

The discrete 1D-FT along the sequence dimension of x ∈ ℝN×D to extract sparse visual features is defined by function Fseq:

xn′=Fseq(xn)=∑k=0N-1xke-2πiNkn,n=0,...,N-1,    (6)

where i represents the imaginary unit and k represents the frequency index. For each value of n from 0 to N−1, the discrete 1D-FT generates a new representation xn′∈ℝD as a sum of all the original input spike features xn∈ℝD. It is important to note that the weights in Equation 6 are fixed constant and can be pre-calculated for all spike sequences.

Similarly, the discrete 2D-FT along the feature and sequence dimensions is defined by function Fseq(Ff):

xn′=Fseq(Ff(xn)),n=0,...,N-1.    (7)

Notably, Equations 6, 7 only consider the real part of the result. Therefore, there is no need to modify the subsequent MLP sub-layer or output layer to handle complex numbers.

3.4 Wavelet transform

Wavelet transform (WT) is developed based on Fourier transform to overcome the limitation of Fourier transform in capturing local features in the spatial domain.

The discrete 1D-WT along the sequence dimension to extract sparse visual features is defined by function Wseq:

xn′=Wseq(xn)=1N[Tφ(0,0)*φ(xn)+∑j=0J-1∑k=02j-1Tψ(j,k)*ψj,k(xn)],    (8) Tφ(0,0)=1N∑k=0N-1xk*φ(xk),  Tψ(j,k)=1N∑k′=0N-1xk′*ψj,k(xk′),    (9)

where n = 0, ..., N−1, N is typically a power of 2, * denotes element-wise multiplication, Tφ(0, 0) are the approximation coefficients, Tψ(j, k) are the detail coefficients, j represents the current scale of wavelet transform with values ranging from 0 to J−1, and k denotes the specific position index of the detail transform. φ(x) is the scaling function, and ψj,k(x)=2j/2ψ(2jx-k) is the wavelet function. Here, we use the Haar scaling function and Haar wavelet function for example, which is defined by the equation:

φ(x)={10≤x<10otherwise,      ψ(x)={1       0≤x<0.5−    1      0.5≤x<10      otherwise,       (10)

Similarly, the discrete 2D-WT along the feature and sequence dimensions is defined by function Wseq(Wf):

xn′=Wseq(Wf(xn)),n=0,...,N-1,    (11)

In the subsequent experimental section, we also delve into the exploration of different basis functions as well as their potential combinations.

4 Method

Following a standard vision transformer architecture, the vanilla spikformer incorporates several key components, including the spiking patch splitting (SPS) module, spikformer encoder layers, and a classification head for visual classification tasks. Here, we directly replace vanilla SSA head with the FW head to efficiently manage spike-form features.

In the following sections, we provide an overview of our proposed FWformer in Figure 1, followed by a detailed explanation of the FW head. Finally, we compare the time complexity of both of these two heads.

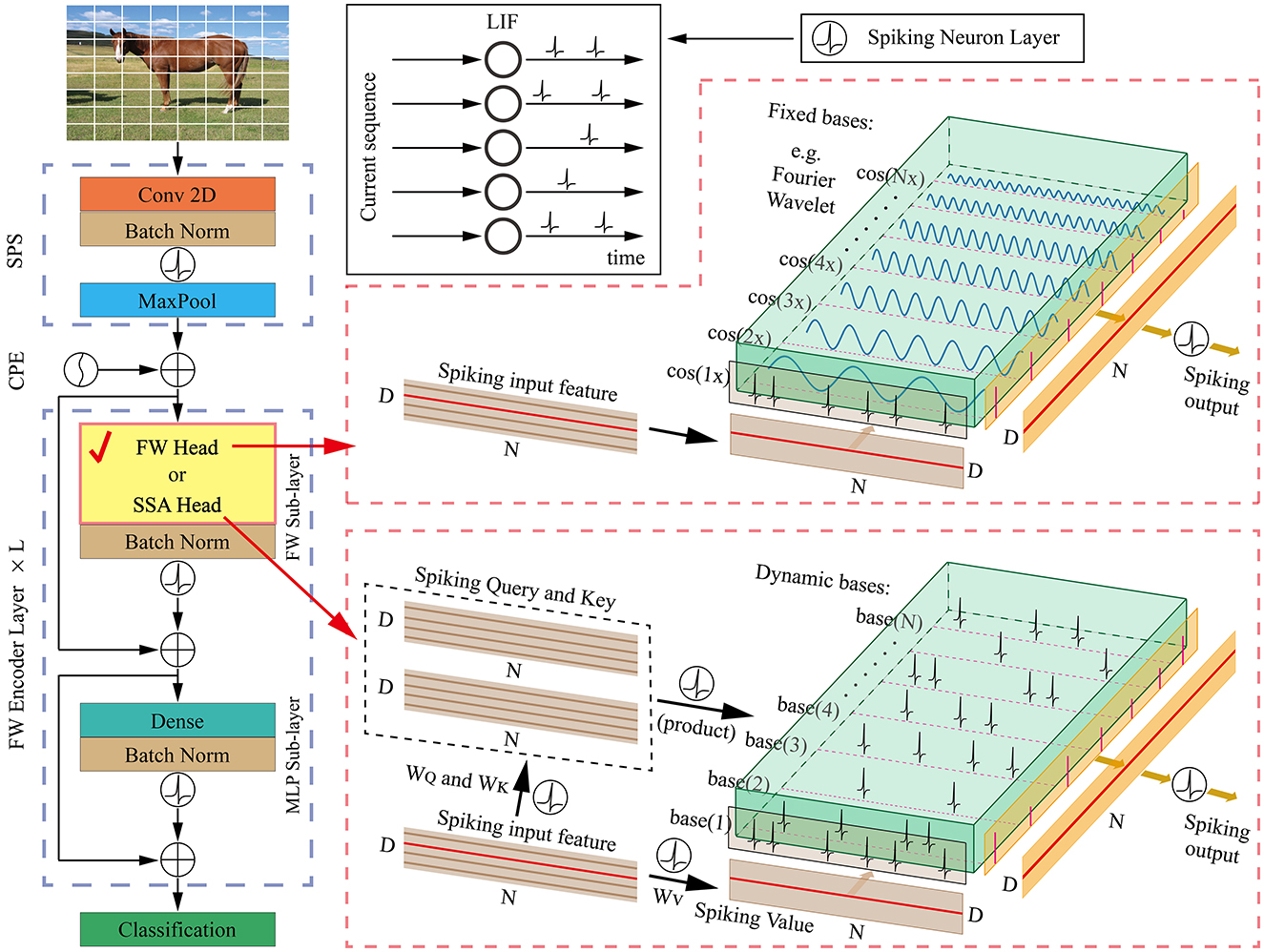
Figure 1. The overall architecture of our proposed FWformer. It mainly consists of three components: (1) spiking patch splitting (SPS) module, (2) FWformer encoder layer, and (3) classification layer. Additionally, we highlight the similarities between the FW head and SSA head at a single time step, which inspires us to choose the former as an exploration for more efficient calculations within the spike-form framework.

4.1 Overall architecture

We provide Figure 1 for an overview of our FWformer. First, for a given 2D image sequence I ∈ ℝT×C×H×W. In the event-based video datasets, the data shape is I ∈ ℝT×C×H×W, where T, C, H, and W denote the time step, channel, height, and width, respectively. In static datasets, a 2D image Is∈ℝC×H×W needs to be repeated T times to form an image sequence. The goal of the spiking patch splitting (SPS) module is to linearly project it into a D-dimensional spike-form feature and split this feature into a sequence of N flattened spike-form patches P ∈ ℝT×N×D. Following the approach of the vanilla spikformer, the SPS module employs convolution operations to introduce inductive bias (Xiao et al., 2021).

Second, to generate spike-form relative position embedding (RPE), the conditional position embedding (CPE) generator (Chu et al., 2021) is utilized in the same manner as the spikformer. The RPE is then added to the patch sequence P, resulting in X0∈ℝT×N×D.

Third, the L-layer FW encoder is designed to manage X0. Different from spikformer encoder layer with SSA head, our FW encoder layer consists of an FW sub-layer and an MLP sub-layer, both with batch normalization and spiking neuron layer. Residual connections are also applied to both the modules. The FW head in FW sub-layer serves as a critical component in our encoder layer, providing an efficient method for spike-form sparse representation. We have provided two implementations for FW head, including Fourier transform (FT) and wavelet transform (WT). Many works in the past have used FT and WT to alternate between the spatial and frequency domains, allowing for efficient analysis of signals. While in this article we treat them as structured basis functions with prior knowledge for information transformation. These implementations will be thoroughly analyzed in the next section.

Finally, following the processing in spikformer, a global average-pooling (GAP) operation is applied to the resulting spike features, generating a D-dimensional feature. The feature is then fed into the classification module consisting of a spiking fully connected (SFC) layer, which produces the prediction Y. The formulation of our FWformer can be expressed as follows:

Xl′=SN(BN(FW(Xl-1)))+Xl-1,    (15) Xl=SN(BN(MLP(Xl′)))+Xl′,    (16) Y=SFC(GAP(X