Cardiometabolic diseases, including cardiovascular disease and metabolic syndrome, are major global health concerns. They significantly contribute to the global burden of disease and mortality, impacting not only individual health but also societies, health systems, and economies on a global scale (Miranda et al., 2019; Rao, 2018). Numerous studies have identified a range of risk factors that contribute to the development and progression of cardiometabolic diseases. These factors arise from a complex interplay of lifestyle choices, genetic predispositions, and pre-existing conditions such as obesity, hypertension, inflammation, insulin resistance, type 2 diabetes, and dyslipidemia (Valenzuela et al., 2023; Kälsch et al., 2015; Wilson and Meigs, 2008).

Understanding the interconnections among these factors in a causal manner is essential for gaining insights into the mechanisms at play and accurately assessing an individual’s risk profile. This knowledge empowers clinicians to make informed decisions and aid researchers in the development of interventions and prevention strategies that are both effective and tailored to the specific needs of each patient.

Traditionally, causality has been established through experimental studies, following the Bradford-Hill considerations on causality (Höfler, 2005). However, conducting controlled experiments on humans presents significant challenges and ethical limitations, especially when addressing long-term effects and interventions that may necessitate lifestyle changes or carry health risks for participants. In this work, we aim to identify the causal relationships among various cardiometabolic risk factors observed in the Health Survey of São Paulo with a Focus on Nutrition Study (2015 ISA-Nutrition), a comprehensive epidemiological study conducted in São Paulo, Brazil (Fisberg et al., 2018). Observational studies are invaluable tools for gaining insights into the complexities of the real world, but they face critical challenges due to biases. Significant statistical associations among variables do not always indicate causality; they may, in fact, be entirely spurious, originating from confounding factors or other issues such as selection bias. This complexity emphasizes the need for rigorous methodologies to address biases in causal inference from observational data.

For our analysis, we consider Judea Pearl’s framework of causation (Pearl, 2000a). This framework represents a seminal advancement in data analysis, enabling us to move beyond mere correlations and discern causal relationships directly from observational data, thus reflecting the rigor typically associated with controlled experiments. Causality is articulated in an intuitive manner: a variable X is considered a cause of another variable Y if an intervention on X (e.g., setting it to a specific value, X=x) results in an expected change in Y. Notably, certain causal discovery algorithms are capable of identifying, despite hidden confounding, the graphical structure of the class of causal models that may have generated the observed data (Zhang, 2008b). These algorithms, complemented by emerging tools for effect identification from their outputs (Maathuis and Colombo, 2015; Perkovi et al., 2018; Jaber et al., 2022), have paved the way for a powerful, data-driven approach to causal inference.

As our primary methodological contribution, we propose the anchor Fast Causal Inference (anchorFCI) algorithm, designed to robustly uncover causal relationships among a set of variables by leveraging an additional set comprising only non-ancestors (non-causes) of the variables of interest. This is achieved by strategically selecting reliable anchors and integrating knowledge of their non-ancestral relationships into the conservative Really Fast Causal Inference (RFCI) algorithm (Colombo et al., 2012), renowned for its effectiveness and robustness in scenarios with latent confounding and limited sample sizes. Specifically, anchorFCI identifies as reliable anchors those variables from the additional set that are significantly associated with the variables of interest and form unambiguous triplets during the conservative orientation phase of the algorithm. Then, it incorporates knowledge of their non-ancestral relationships as outlined in Section 2.4.2. AnchorFCI not only enforces the appropriate arrowheads but also utilizes an adapted skeleton phase that prevents conditional independence tests between anchor variables conditioned on non-anchor variables. This adaptation is vital for preserving the integrity of the encoding of the conditional independencies implied by the final graph while reducing the number of required conditional independence tests, thereby enhancing the algorithm’s scalability and robustness.

Our proposed approach is particularly well-suited for causal discovery among phenotypes, clinical factors, and sociodemographic variables when information on genetic variants, such as single nucleotide polymorphisms (SNPs), is available. This is because we can leverage the well-established understanding that genotypes are not influenced by any of the non-genetic variables. It is crucial to emphasize that, while this approach shares some similarities with Mendelian randomization principles (Davey Smith and Hemani, 2014; Ribeiro et al., 2016), it does not assume that SNPs identified as anchors are valid instruments (de Leeuw et al., 2022). Rather, the anchorFCI algorithm solely relies on conditional independence tests to identify genetic anchor variables and uncover causal relationships.

In analyzing the 2015 ISA-Nutrition dataset, our approach has successfully unveiled the causal connections among all examined phenotype and clinical variables, by leveraging SNPs identified in Genome-Wide Association Studies (GWAS). Furthermore, by employing effect identification tools, we have successfully identified and estimated the causal effects associated to all uncovered causal relationships. The results corroborate numerous well-established relationships, while also providing a deeper understanding of the intricate network of connections among various cardiometabolic risk factors. Additionally, they demonstrate the potential of robust data-driven causal inference methods in addressing complex and multifactorial diseases, paving the way for the development of more effective interventions and treatments.

Our analysis focused on 681 individuals who were not genetically closely related, selected from a total of 841 participants in the 2015 Health Survey of São Paulo with a Focus on Nutrition Study (2015 ISA-Nutrition) – a subset of the cross-sectional population-based 2015 Health Survey of São Paulo (2015 ISA-Capital). The primary goal of the 2015 ISA-Nutrition study is to investigate the relationships between lifestyle choices, biochemical markers, and genetics in the development of cardiometabolic diseases among residents of São Paulo city, the largest Brazilian city located in the Southeastern region of the country. For more comprehensive information about the study, refer to Fisberg et al. (2018).

The survey targeted a probabilistic sample of individuals age ≥12, residing in permanent households within the urban area of São Paulo city, excluding those who were pregnant or lactating. The sampling process involved two stages with stratification by clusters (urban census tracts and households) to ensure representative coverage at the population level. During the year of 2015, ISA-Capital collected sociodemographic data, information regarding the use of health services, lifestyle, and other relevant information through a structured questionnaire administered in the households by trained interviewers (Alves et al., 2018). Anthropometric data, blood pressure measurements, and blood samples were collected by trained nurses during a second visit to the participant’s household. Detailed protocols for these measurements are also available in Fisberg et al. (2018).

Genomic DNA was obtained from peripheral blood samples extracted by automated method. SNPs were assessed using the AxiomTM 2.0 Precision Medicine Research Array in the Thermo Fisher Scientific Laboratory (Affymetrix Inc., Santa Clara, CA).

This study has been conducted according to the principles expressed in the Declaration of Helsinki and was approved by the Ethics Committee on Research of the School of Public Health of the University of São Paulo (#30848914.7.0000.5421). All participants authorized their genotyping and signed a written informed consent/assent before entering the study and, if they were adolescents, also their proxies. The data and samples were anonymized after collection.

The 2015 ISA-Nutrition study incorporates genetic data from 841 individuals, with some being relatives. Notably, conducting causal analysis on samples from genetically or familial-related individuals necessitates careful consideration of the underlying dependence structure among them (Ribeiro and Soler, 2020). Since addressing this issue is beyond the scope of this study, we excluded individuals who might share a parental relationship, resulting to a final sample size of 681 individuals. Specifically, the genomic relationship matrix (GRM) was computed for all 841 individuals and our analysis was limited to individuals with a genetic distance of ≤0.125, indicating relationships beyond second-degree relatives.

The dataset comprises a diverse array of sociodemographic, clinical, and genetic data. Additionally, it includes principal components of global ancestry allowing for adjustment for population stratification effects. This adjustment is particularly crucial in highly admixed populations such as the Brazilian population. The principal components of global ancestry are estimated using a larger set of SNPs across the genome of the ISA-Nutrition participants and the 1,000 Genome Project reference data, utilizing the software PLINK 2.0 and R (SNPRelate package to control for population stratification). More details of genetic evaluation of ISA-Nutrition data are available in Pereira et al. (2024).

In our analysis, we regarded sex, age, and the first two components of global ancestry as standard covariates. Additionally, we selected variables representing lifestyle factors, biochemical markers, and health conditions acknowledged as pertinent by domain experts. Moreover, SNP data was utilized in identifying genetic anchors crucial for causal analysis among the phenotypic variables.

The variables referring to lifestyle factors, biochemical markers, and health conditions included in the analysis are described below:

Obesity is defined based on the body mass index (BMI), given as weight (kg)/height (m)2. An adult is obese if their BMI ≥ 30 kg/m2 (WHO Consultationm, 2000). In adolescents, obesity is identified when their BMI-for-age surpasses two standard deviations (2SD) above the mean, which, for a 19-year-old, corresponds to a BMI of 30 kg/m2 (Onis et al., 2007).

It is considered positive if fasting blood glucose is >126 mg/dL or if medication for T2D (indicated by the binary variable Med_T2D) is being used, which includes hypoglycemic agents and/or insulin therapy (Cobas et al., 2022).

For adults, hypertension is diagnosed when systolic blood pressure is elevated (≥ 140 mmHg), diastolic blood pressure is elevated (≥ 90 mmHg), or if antihypertensive drugs (indicated by the binary variable Med_HTN) are being used (Barroso et al., 2021). For adolescents aged 12 and 13 years, the cutoff points for systolic or diastolic blood pressure are defined as the 95th percentile based on sex, age, and height. For individuals aged 14–19 years, the cutoffs were set at systolic blood pressure (SBP) ≥ 130 mmHg or diastolic blood pressure (DBP) ≥ 80 mmHg (Flynn et al., 2017).

The concentration of C-reactive proteins in the blood, obtained through a blood test, serves as a biomarker of inflammation in the body. It is measured in milligrams per deciliter (mg/dL), with the normal range typically falling below 1 mg/dL (Ridker, 2003).

HOMA-IR is calculated using the formula: fasting plasma insulin (μU/mL) × fasting plasma glucose (mmol/L)/22.5. The cutoff point for HOMA-1R, proposed by Geloneze et al. (2009) and validated for the Brazilian population, is set at 2.71 (Golbert et al., 2019).

They are all measured using a colorimetric enzymatic method with reagents from Cobas–Roche Diagnostics GmbH (Mannheim, Germany). The normal ranges are typically as follows: TGL ideally below 150 mg/dL (adults) and 130 mg/dL (adolescents), LDLc ideally below 160 mg/dL (adults) and 130 mg/dL (adolescents), and HDLc ideally above 40 mg/dL (men), 50 mg/dL (women), and 45 mg/dL (adolescents) (Précoma et al., 2019; Giuliano et al., 2005).

Dyslipidemia is classified as positive if the individual is taking lipid-lowering medication (indicated by Med_DLP) or if any of the following conditions are met: elevated LDLc levels (≥ 160 mg/dL for adults and ≥ 130 mg/dL for adolescents), elevated TGL levels (≥ 150 mg/dL for adults and ≥ 130 mg/dL for adolescents), or low HDLc levels (men < 40 mg/dL, women < 50 mg/dL, and < 45 mg/dL for adolescents) (Précoma et al., 2019).

A binary variable indicating whether the individual meets the total physical activity recommendations across four domains–work, domestic activities, transportation, and leisure–as outlined in the 2010 Global Recommendations on Physical Activity for Health (World Health Organization, 2010).

Additionally, variables indicating use of Medication for T2D (Med_T2D), Medication for HTN (Med_HTN), and Medication for DLP (Med_DLP) were included in the analysis.

Among the existing algorithms, the Fast Causal Inference (FCI) (Spirtes et al., 2001), combined with the complete set of orientation rules by Zhang (2008b), stands out for its rigorous foundational principles and minimal reliance on assumptions compared to other methods. Since the introduction of the FCI, a range of strategies and adaptations have emerged to tackle scalability and robustness in scenarios of limited data. These include the anytime FCI by Spirtes (2001), the RFCI by Colombo et al. (2012), and their conservative counterparts (Colombo and Maathuis, 2014). Crucially, these algorithms do not require causal sufficiency, demonstrating their effectiveness in managing latent confounding. This capability makes FCI-like algorithms highly suitable for analyzing real-world datasets.

Relying solely on a reliable conditional independence test, the FCI and its variants learn a Partial Ancestral Graph (PAG) representing the class of all causal models that entail the set of observed conditional independencies, referred to as the Markov equivalence class (MEC). In a PAG, tails and arrowheads represent, respectively, ancestral (causal) and non-ancestral (non-causal) relationships common to all models within the most plausible MEC. A circle (“o”) denotes a non-invariant edge mark, indicating that within the MEC, there is a model where the edge mark is a tail and another model where the same edge mark is an arrowhead. Remarkably, the output is ensured to be asymptotically sound and complete, even in scenarios involving unobserved confounding and selection bias.

Scalability and integration of background knowledge are major challenges in causal discovery under latent confounding. While increasing the number of variables in the graph can boost discovery power, the reliability of the inferences often decreases due to statistical instabilities. Moreover, merely enforcing edge marks can lead to incorrect downstream orientations and violations of the equivalence class representation if the algorithm is not properly adapted. Currently, no complete strategy exists for integrating general background knowledge into the FCI framework. This integration has only been explored in specific contexts, such as studies with time series data (Gerhardus and Runge, 2020) or certain types of knowledge, such as tired (known causal order) or local knowledge (Andrews et al., 2020; Wang et al., 2022).

In this work, we introduce anchorFCI, a novel adaptation of the conservative RFCI designed to strategically identify reliable anchors and effectively integrate them with their known non-ancestral relationships. As detailed in Section 2.4.2, anchorFCI operates on two variable sets: the first contains the variables of interest, while the second comprises variables that are not caused by any from the first. It begins by identifying reliable anchors, defined as variables Vi from the second set that are significantly associated with a variable Vj from the first set and form unambiguous triplets during the algorithm’s conservative orientation phase. Next, it performs an adapted skeleton phase that ensures a consistent selection of d-separators while remaining order-independent, as it is based on the stable skeleton algorithm by Colombo and Maathuis (2014). Finally, it enforces arrowheads on the appropriate edges Vi◦−→ Vj according to the established non-ancestral relationship between the two variable sets. Notably, strategies for managing conflicting orientations and limiting conditioning set sizes, as detailed in Section 2.4.1, are integral features of the RFCI and, thus, can be easily adjusted through parameters in the anchorFCI function. The algorithm is publicly available as an R package on GitHub at https://github.com/adele/anchorFCI and it leverages the RFCI implementation from the pcalg R package (Kalisch et al., 2024).

We apply the anchorFCI algorithm with strategies to enhance robustness to uncover causal relationships among the 14 phenotypic and clinical variables outlined in Section 2.2. The algorithm identifies anchors from SNPs that are significantly associated with phenotypes of interest through GWAS, and incorporates knowledge of their non-ancestral relationships. This approach not only improves robustness but also boosts discovery power by facilitating the identification of additional causal relationships. To account for confounding effects related to sex, age (both original and squared), and the first two principal components of global ancestry, these covariates will be included in all necessary tests of conditional independence.

Despite the significant potential of causal discovery algorithms, they present considerable challenges in terms of scalability to larger graphs and robustness to statistical errors. Firstly, the number of potential causal structures grows super-exponentially with the number of variables, rendering the problem computationally NP-hard (Chickering et al., 2004). Achieving scalability to large graphs, particularly in scenarios involving latent confounding, necessitates reliance on model assumptions. These may include enforcing sparsity and constraining the size of conditioning sets (Claassen et al., 2013).

Moreover, the majority of the existing algorithms, including the FCI and its variants, rely on the assumption of faithfulness, which posits that the independencies inferred from data accurately represent the true underlying model. Notably, any falsely identified independencies can lead to conflicting orientations and inconsistencies in the implied conditional independencies (Zhang and Spirtes, 2008; Zhalama et al., 2017). This poses a significant challenge for real-world applications, particularly when dealing with limited sample sizes, as statistical tests may lack sufficient power to accurately identify potentially weak or noisy associations. This issue becomes more pronounced when dealing with larger graphs (e.g., 10 or more variables), exemplifying the curse of dimensionality, as it leads to an increased number of conditional independence tests and a significant decrease in statistical power as the conditioning set size grows.

To minimize issues arising from unfaithfulness, we employ the following two strategies:

• Conservative edge orientations with majority rule: as proposed by Colombo and Maathuis (2014), edge orientations are strictly conducted conservatively, meaning that they exclusively rely on triplets that have been previously determined as unambiguous. To assess the ambiguity of an unshielded triplet (i.e., three variables where the first and second, and the second and third, are adjacent, but not the first and third), additional conditional independence tests are performed. These tests aim to detect errors in determining whether the second variable belongs or not to the set that renders the first and third variables independent of each other, potentially due to instances of unfaithfulness. With the majority rule approach, the decision is based on the majority of the involved conditional independence tests. In the event of a tie, the triplet is deemed ambiguous, and no orientation is conducted.

• Constrained conditioning set size: as pointed out by Spirtes (2001) and Colombo et al. (2012), the accuracy of the FCI significantly decreases when relying on independencies conditional on a large set of variables, as, in such cases, statistical errors due to the low power of the tests become inevitable, especially with small sample sizes. They also demonstrate that restricting the size of conditioning sets in the independence tests does not compromise the correctness of the output PAG; it may only lead to a less informative PAG. In light of this result, the RFCI not only accepts a constraint on the size of the conditioning sets, but also employs a procedure that requires fewer conditional independence tests than the FCI. The authors demonstrated the RFCI’s consistency in sparse scenarios, showing that by avoiding statistical tests with the least power (i.e., those with relatively large conditioning sets), the results become notably more reliable, particularly for small sample sizes.

2. Skeleton inference with an adapted search for minimal d-separating sets: In the initial phase of the algorithm, known as the adjacency phase, the model’s skeleton is inferred through a series of conditional independence tests. Whenever a pair of variables is found to be conditionally independent given a set of other variables, such separating set is considered minimal and the edge connecting them is removed. In this phase, it is essential to prevent the algorithm from performing independence tests between two variables from the second set (e.g., two SNPs) conditional on any variable from the first set (e.g., a phenotype). Notably, this restriction does not compromise the correctness or completeness of the algorithm. This can be demonstrated through a direct application of (Tian et al., 1998, Theorem 2), which states that if a set Z d-separates two variables X and Y, we can get a smaller d-separator Z′ by removing from Z all nodes that are not ancestors of X or Y. This implies that, since the first set consists entirely of non-ancestors of the second set, any faithful minimal separating set for a pair of variables from the second set will necessarily exclude variables from the first set.

3. Enforcing known arrowheads: During the orientation phase of the algorithm, edge-mark inference rules (R0 to R10, as detailed in Zhang (2008b)) are sequentially applied until they can no longer be utilized. Throughout this phase, we ensure that every edge connecting a variable Vi from the first set (e.g., a SNP) and a variable Vj from the second set (e.g., a phenotype) is oriented with an arrowhead pointing towards Vj. In other words, these edges will take the form Vi∗→Vj, where ∗ denotes any edge mark that the algorithm may learn. Incorporating this type of background knowledge is straightforward and can be achieved simply by applying the rules once the known edge marks are enforced and then checking the validity of the PAG as an ancestral graph (i.e., no cycles or almost cycles). Notably, the integration of non-ancestral knowledge in the context of time-series data (Gerhardus and Runge, 2020) showcases the potential to enhance both robustness and learning capabilities in causal discovery.

Notably, when applied to a dataset comprising SNPs and phenotype variables, the resultant PAG from the anchorFCI algorithm will exclusively include edges between an SNP and a phenotype falling into one of the following types: SNP ↔ Phenotype (indicating purely spurious association), SNP → Phenotype (indicating a causal SNP), or SNP ◦→ Phenotype (indicating there is not sufficient evidence to determine whether the SNP is a cause or only spuriously associated with the phenotype).

By integrating inherently unambiguous orientations, anchorFCI not only prevents discrepancies with established non-ancestral knowledge, potentially induced by violations of faithfulness, but also boosts discovery power by facilitating the conservative identification of additional causal relationships.

To further illustrate how anchorFCI can achieve greater robustness and accuracy compared to RFCI, particularly in limited data settings where the faithfulness assumption is likely to be violated, we selected a dataset from our simulation study, as detailed in Section 2.4.4. The dataset consists of 1,000 samples, generated based on the Maximal Ancestral Graph (MAG) shown in Figure 1A. The variables ≺, with ≺ denoting precedence in the partial ordering. The corresponding true PAG, obtained without using the partial order information, is shown in Figure 1B.

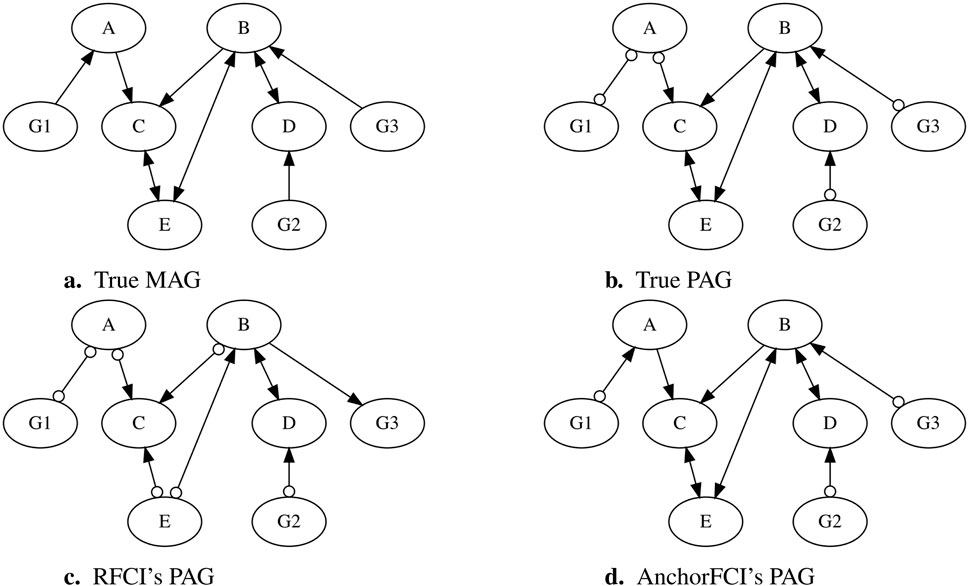
Figure 1. Comparison of PAGs inferred by RFCI and anchorFCI using a simulated dataset. The dataset was generated based on the MAG in (A), structured as G1,G2,G3≺A,B,C,D,E. The true PAG is presented in (B), while the PAGs inferred by RFCI and anchorFCI are shown in (C, D), respectively.

When applying the conservative RFCI algorithm with the majority rule, we obtain the PAG in Figure 1C. The collider triplets ⟨A,C,B⟩, ⟨E,B,D⟩, ⟨A,C,E⟩, and ⟨G2,D,B⟩ are identified as unambiguous and correctly oriented. The triplets ⟨G1,A,C⟩ and ⟨G3,B,C⟩ are identified as unambiguous non-collider triplets, however, without the partial order information, their orientations cannot be determined. The triplet ⟨C,B,D⟩ is marked as ambiguous. After applying the remaining orientation rules, RFCI incorrectly orients B→G3, violating the known, but unused, information that G3≺B. The resulting PAG has a Structural Hamming Distance (SHD) of five from the true PAG, reflecting the number of incorrect orientations.

In contrast, when applying anchorFCI, we obtain the PAG in Figure 1D, which not only accurately captures all the oriented edges from the true PAG but also correctly identifies additional orientations from the original MAG. First, variables G1, G2, and G3 are all identified as reliable anchors, as they form unambiguous triplets ⟨G1,A,C⟩, ⟨G2,D,B⟩, and ⟨G3,B,C⟩. Then, after applying the adapted skeleton algorithm, anchorFCI integrates the known non-ancestral relationships by orienting G1◦→A, G2◦→D, and G3◦→B. This not only avoids the mistakes made by RFCI but also enables the accurate orientation of the edge B→C and of the collider ⟨C,E,B⟩. Notably, anchorFCI also infers the tail on A→C, indicating that A is a definite cause of C, thereby learning a representation that goes beyond the MEC.

To test conditional independence between binary (obesity, T2D, HTN, DLP, physical activity, and medication variables), continuous (CRP, HOMA-IR, TGL, LDLc, and HDLc), and multinomial (SNP) variables, we use the symmetric conditional independence test for mixed data proposed by Tsagris et al. (2018), available in the MXM R package (Lagani et al., 2017). This test utilizes linear or generalized linear regression, depending on the nature of the involved variables. Logistic regression is employed for binary outcomes, Gaussian linear regression for continuous outcomes, and multinomial log-linear regression for multinomial outcomes. To prevent departures from normality in tests involving continuous variables, we transformed them using the rank-based inverse normal transformation available in the RNOmni R package (McCaw, 2023). Missing values were imputed using MissForest, a non-parametric method for imputing mixed-type data sets by employing random forests (Stekhoven and Bühlmann, 2012). We utilized the implementation of the MissForest algorithm available in the MissRanger R package (Mayer and Mayer, 2019), setting the number of forests to 500.

Formally, Tsagris et al. (2018) test evaluates the conditional independence of two variables, Vi and Vj, given a set of variables Sij, by testing two null hypotheses: H01:P(Vi|Sij)=P(Vi|Vj,Sij) and H02:P(Vj|Sij)=P(Vj|Vi,Sij). The null hypothesis H01 is tested using a nested likelihood-ratio test comparing a reduced model (where Vi is regressed on Sij) against a full model (where Vi is regressed on both Sij and Vj). Similarly, H02 is tested by reversing the roles of Vi and Vj. In general, the p-values p1 and p2 from the tests for H01 and H02, respectively, tend to be identical only asymptotically. To correct for any potential asymmetry in limited data scenarios, we adopt Tsagris et al. (2018) strategy of merging dependent p-values. Such method calculates the combined p-value as min(2×min(p1,p2),max(p1,p2)) and has demonstrated superior learning accuracy when compared to alternative methods.

All tests include sex, age (original and squared), and the first two principal components of global ancestry in the conditioning set, ensuring comprehensive adjustment for these variables. Importantly, these variables stand out as special covariates because they are not caused by any other variables, and thus, conditioning on them can never introduce biases such as collider bias (Holmberg and Andersen, 2022).

Finally, all tests were conducted with a significance level set at 5%, without applying any correction for multiple comparisons. In contrast to association studies, which aim to validate statistical dependencies, causal discovery relies on establishing reliable statistical independencies. It is crucial to note that the non-rejection of the null hypothesis (indicating conditional independence) does not imply the acceptance of the alternative hypothesis (indicating conditional dependence). Any correction aimed at reducing the number of falsely identified associations may significantly increase the number of falsely identified independencies, thereby triggering a cascade of erroneous edge orientations. Conversely, as noted by Spirtes (2001); Colombo et al. (2012), false associations often prevent certain edge orientations, leading to a final PAG that, while less informative, still tends to uphold accuracy.

To quantitatively assess the enhanced robustness and discovery power of anchorFCI compared to the conservative RFCI, we designed a simulation study. To capture diverse scenarios, we simulated 50 unique random MAGs with eight nodes, structured as ≺. Additionally, to account for varying degrees of unfaithfulness, we generated 30 datasets for each MAG, with sample sizes N=500,1000,5000,10000. The variables G1,G2,G3 are modeled as discrete variables, each with three levels, following a multinomial distribution, while A,B,C,D,E are continuous variables, following a Gaussian distribution. The datasets were generated using the simMixedDAG R package (Lin, 2019), where each variable is modeled as a linear combination of its parents (including potential latent variables), with randomly assigned coefficients. The choice of distributions does not impact the comparison between the algorithms but was selected to reflect typical applications involving genotype and phenotype variables.

Since anchorFCI aims to enhance causal discovery among the variables of interest by selecting reliable anchors from , we evaluate the algorithms using a score based on the Structural Hamming Distance (SHD) computed considering exclusively edges among the variables of interest. Given that anchorFCI can identify orientations beyond those in the true MEC’s PAG (i.e., the one obtained without using any partial order information), this score allows us to assess both the accuracy and informativeness of the inferred PAG. It is calculated as the difference between the SHD of the inferred PAG relative to the true MAG, and the SHD of the true MEC’s PAG relative to the true MAG. Smaller scores indicate higher accuracy, with zero indicating the inferred PAG is as informative as the true MEC’s PAG (i.e., the one obtained without using any partial order information), and negative values indicating the inferred PAG is more informative than the true MEC’s PAG.

A necessary condition for identifying the causal effect of a variable X on a variable Y is that the edge X→Y is visible, indicating that X and Y do not share any latent causes This condition can be easily verified through a graphical criterion presented by Zhang (2008a).

The generalized backdoor criterion (Maathuis and Colombo, 2015) is regarded as one of the most straightforward effect identification graphical criteria. It states that the causal effect of a variable X on a variable Y can be identified from a PAG P if there exists a set Z, comprising solely non-descendants of X, that blocks (in the sense of d-separation–see Pearl (2000b)) all definite-status backdoor (confounding) paths between X and Y in P. In this case, the post-interventional probability distribution of a variable Y after an intervention that sets X=x, denoted do(X=x), is expressed by:

Such an integral can be estimated from N observational samples i=1N as following:

where f̂(x,z)=P̂(Y=y|X=x,Z=z) can be readily obtained through (generalized) regression analysis of Y on X and Z. Note that if Z=∅ is admissible for backdoor adjustment, the interventional distribution simplifies to P(Y=y|do(X=x))=P(Y=y|X=x), which can also be readily obtained using (generalized) regression analysis of Y on X. If continuous response variables are (natural) log-transformed before regression analyses to normalize residual distributions, then estimates are subsequently back-transformed to the original scale using the improved Cox’s method proposed by Olsson (2005). Effect sample sizes for each prediction are determined using the methodology by Thomassen et al. (2024).

In cases where the generalized backdoor criterion does not apply, alternative tools for causal effect identification and estimation from PAGs are available. These include the generalized adjustment criterion, introduced by Perkovi et al. (2018), and the complete causal calculus and (conditional) complete effect identification algorithm developed by Jaber et al. (2022).

The proportions of binary health conditions vary: 23.2% of individuals are obese, 14.7% have T2D (with 70% of them taking medication for T2D), 45.8% have HTN (with 53.4% of them taking medication for HTN), and 66.7% have DLP (with 12.8% of them taking medication for DLP). Moreover, 68.8% of individuals fulfill the 2010 WHO recommendations for total physical activity (Bull et al., 2020). Summary statistics for the cont