1 Introduction

Millions of individuals globally experience the debilitating effects of neurological disorders, which significantly impact their cognitive and/or motor functions (World Health Organization, 2020). While there is a growing array of technologies and solutions being developed for the treatment of these conditions, they often only serve to slow progression or alleviate symptoms (Chin and Vora, 2014; French et al., 2016).

In addition to medical interventions involving chemical processes, artificial devices are being developed to enhance the quality of life for individuals. Bringing neuroprostheses to realization requires consideration of the behavior of biological neurons and their connections and interactions with artificial neural networks. Consequently, investigating the interaction of neuronal cell assemblies is necessary to comprehend and replicate specific behaviors driven by intrinsic spontaneous activity. Moreover, achieving long-term replacement of damaged brain regions with artificial devices necessitates an understanding of their neurophysiological behaviors.

In this context, there is a pressing need for new therapeutic approaches and technologies aimed at promoting cell survival and regenerating local circuits (Farina et al., 2021), as well as restoring long-distance communication between disconnected brain regions and circuits (Bouton et al., 2016). Therefore, the characterization and modeling of biological neural networks (Panuccio et al., 2018; Semprini et al., 2018) are crucial for the development of a new generation of neuroprostheses. These prostheses aim to mimic biological dynamics and provide adaptive stimulation at biological timescales, following the principle of electroceutics (Famm et al., 2013; Reardon, 2014; Donati and Valle, 2024).

With the advent of new neuromorphic platforms, conducting biohybrid experiments is gaining increasing relevance. This is not only crucial for advancing neuromorphic biomedical devices (Famm et al., 2013; Reardon, 2014) but also for gaining insights into the mechanisms of information processing in the nervous system. Recent advancements in neuroprostheses have significantly contributed to this progress (Panuccio et al., 2018; Semprini et al., 2018). Neuromorphic devices now have the capability to receive and process input, while also delivering their output locally or remotely through various means such as electrical, chemical, or optogenetic stimulation (Christensen et al., 2022).

The significant advancements in bioelectronics and neuroprosthetics resulted in technologies able to replace and retrain either brain (Chiappalone et al., 2022) or somatosensory functions (Raspopovic et al., 2021; Iberite et al., 2023), block seizures in epilepsy (Geller et al., 2017), and relive symptoms in neurodegenerative diseases such as Parkinson's disease (Pycroft et al., 2018; Milekovic et al., 2023).

In order to conduct bi-directional biohybrid experiments and devise bioelectrical therapeutic solutions for healthcare, such as electroceutics (Famm et al., 2013; Reardon, 2014; Donati and Valle, 2024; Di Florio et al., 2023), it is essential to incorporate real-time bio-physics interfaces and SNN processing. These components are imperative to facilitate interactions at the biological time scale (Corradi and Indiveri, 2015; Sharifshazileh et al., 2021).

A new generation of neuro/brain prostheses, termed “twins”, has emerged with the capability to replace damaged brain tissue. These innovations span from peripheral interventions (Donati and Valle, 2024; Valle et al., 2018; Romeni et al., 2020) to central nervous system interfaces (Rowald et al., 2022). Despite primarily existing as proof of concepts, neuromorphic twins hold promise for revolutionizing healthcare (Donati and Valle, 2024; Buccelli et al., 2019; Keren et al., 2019; Mosbacher et al., 2020; Beaubois et al., 2024).

Hence, this generation of neuroprostheses pushes the need for biophysically detailed neuron model. For instance, as disorders in nervous system and neuronal network can be induced from ion channel morphology (Lai and Jan, 2006; Spillane et al., 2016), the capability to reproduce the shape of the action potential with biophysical detail and biological meaningfulness to relate changes in its shape to biophysical values is important. Consequently, the most suitable candidate is the Hodgkin-Huxley (HH) paradigm (Hodgkin and Huxley, 1990) that is one of the most biologically meaningful model (Izhikevich, 2004; Brette, 2015).

While the single compartment HH model is mostly used over multicompartment model, as it is simpler and less resource-intensive, it remains limited due to its inability to capture the complex morphology of neurons (Beaubois et al., 2022). In contrast, multicompartment models offer a more comprehensive and biologically realistic approach, thus providing deeper insights into neuronal function and information processing, finding interest in multiple fields from biological interest as a study model for neurological disorders, and learning mechanism to computing interest inspired from the dendritic architecture of the neurons (Markram et al., 2015).

Multicompartmental modeling notably allows the investigation of the role of dendrites in neurons. Dendrites, particularly important regions for vital computations tied to their spatial morphology (Forrest et al., 2018), undergo learning-related changes, as evidenced in dendritic compartments (Godenzini et al., 2022). Dendrites also facilitate a greater diversity of presynaptic terminal classes, leading to different learning laws (Froemke et al., 2005; Sardi et al., 2018) and contribute to support diverse information processing strategies in neural networks (Markram et al., 2015). Moreover, they are known to exhibit physiological and morphological abnormalities during postnatal development in motor neurons affected by amyotrophic lateral sclerosis (ALS) (Martin et al., 2013) and marked changes in their structure (Fogarty et al., 2016).

Moreover, studies such as Brette (2015) shows that there are phenomena such as frequency-dependent attenuation of membrane as a function of frequency or the presence of wide variations in voltage which may be induced by the presence of active conductances distributed along the axon and dendrites. Thus, important biophysical phenomena such as spike initiation (Naundorf et al., 2006) in the axon initial segment (AIS) (Debanne et al., 2011) or in the dendrites (Gasparini et al., 2004) can be modeled. Phenomena such as dendritic spikes are, for example, known to play a part in stimulus selectivity in cortical neurons (Smith et al., 2013). Hence, the multicompartmental modeling is undoubtedly crucial to the creation of faithful and reliable model providing enough biological meaningfulness to study neurological disorders through artificial models.

The state of the art in multicompartment Hodgkin-Huxley (HH) neurons has been significantly advanced by the development and continuous updating of software platforms such as NEURON (Carnevale and Hines, 2006; Kumbhar et al., 2019; Awile et al., 2022) or integration of its computing core as in Zhang et al. (2023). NEURON is a simulation environment for modeling individual neurons and networks of neurons, allowing for the creation of complex neural models that incorporate multicompartment HH models mainly scripting in hoc with Python interfaces. While NEURON stands out for its comprehensive features and widespread use in computational neuroscience, other software platforms such as Arbor (Abi Akar et al., 2019) and Brian (Stimberg et al., 2019) also contribute to the landscape of neural simulation. Arbor is optimized for high-performance simulation of large neural networks, emphasizing multicore CPUs and GPUs, while Brian is known for its simplicity and flexibility. Additionally, an other notable GPU implementation is Kobayashi et al. (2021) that explores the use of an explicit solver to reduce computation time. Another implementation using an explicit solver designed for FPGA-based datacenter/cloud paradigm, with a focus on computational power and additional features such as gap junctions, can be found (Miedema et al., 2020; Miedema and Strydis, 2024).

Benefiting from a flexible and real-time architecture identical to BimuS (Beaubois et al., 2024), a real-time biomimetic single compartment SNN, this contribution is intended to propose a novel hardware architecture for multicompartment HH neuron emulation using SoC FPGA promoting ease of use and versatile interconnection. Furthermore, this study takes advantage of High-Level Synthesis (HLS) design methods (Cong et al., 2011; Nane et al., 2015) paired with standard hardware design to improve portability, reduce development time, and open contributions to a larger part of the community. Consequently, this system constitutes a first step toward a real-time multicompartment HH neuron emulation platform on SoC FPGA that could easily integrate biohybrid closed-loop system to explore the electroceutic approach and potentially contribute to the development of neuroprostheses and neuromorphic twins.

2 Materials and methods

This section introduces the system, outlining its architecture and the methods for numerical solving.

2.1 Neuron model

Neurons are multicompartment neurons following the Hodgkin-Huxley (HH) (Hodgkin and Huxley, 1990) paradigm that is based on the one dimensional cable equation applied to the HH paradigm corresponding to Equation 1, thus introducing the spatial dimension x in the equation (Carnevale and Hines, 2006).

12πa∂∂x(πa2Ra∂V∂x)=Cm∂V∂t+IHH    (1)

where a is the radius of the compartment, Ra the resistance of the axon, Cm the membrane capacitance, IHH the currents of the HH model, and V the membrane potential in the middle of the compartment.

Neurons implement ion channels of the Pospischil model (Pospischil et al., 2008) introducing six conductance-based currents and a stimulation current. Neurons are divided in sections that share the same electrical properties and represent different elements of the neuron similarly to Carnevale and Hines (2006) as illustrated in Figures 1A, B. An electrical equivalent circuit of the multicompartmental model using HH paradigm is shown in Figure 1C.

Figure 1. Multicompartment neuron model. (A) Schematic of multicompartment neuron model. (B) Representation of multicompartment modeling showing different parts of the neuron modeled as connected cylinders (sections). (C) Electrical equivalent circuit of multicompartmental neuron model. The neuron is compartmentalized in cylinder of various length and diameters representing different elements of the neuron and their properties. Iinj is the current injected. (D) Spatial discretization of a section where a cable is approximated as a series of connected cylinders named segments (or compartments). Virtual points are added at the extremities of the section to verify the no current leak condition.

The spatial discretization involves the second order correct approximation of ∂2V/∂x2 (Equation 1) equated in Equation 2 (Carnevale and Hines, 2006). A representation showing cable equations discretized using “compartmentalization” that approximates the cable equations by a series of compartments (also called segments) connected by resistors is shown in Figure 1D.

∂2V∂x2≈V(x+Δx)-2V(x)+V(x-Δx)Δx2    (2)

The discretized model can be seen as the computation of spatio-temporally continuous variables over a set of discrete points in space (“grid” of “nodes”) for a finite number of instants in time (Carnevale and Hines, 2006). Therefore, values of functions will refer at points on the grid function equated in Equation 3 (Mascagni, 1990).

Gin≡G(iΔx,nΔt)    (3)

where Δt is the time step and Δx=LN the grid width computed from L the length of the cable and N the number of spatial grid points.

The membrane potential is then evaluated at the middle of each compartment. The boundary condition that states that no axial current flows at the ends of the cable is respected by adding virtual points at the extremities of the cable.

While the use of explicit methods is suggested to be applicable for multicompartmental model solving according to Kobayashi et al. (2021), explicit methods remain limited for real-time systems because of the significant constraint imposed by the very small time step required. While the explicit Runge-Kutta-Chebyshev method with a very small time step is shown stable for multicompartment modeling (Kobayashi et al., 2021), simpler explicit solvers of lower accuracy as the Forward Euler used for the single compartment modeling are known unstable for multicompartment modeling (Carnevale and Hines, 2006).

A numerically stable solver appropriated for stiff systems and widely used is the Crank-Nicholson method. It relies on an evaluation at half a time step using Backward Euler advanced over the full interval with Forward Euler and is known stable and accurate (Carnevale and Hines, 2006; Hines, 1984). The equation applied to the membrane potential is equated in Equation 4.

Vin+1=2Vin+12-Vin    (4)

The second order correct and numerically stable solution of the finite difference form of Equation 4 is expressed in Equation 5 as a tridiagonal linear system evaluated at half a time step.

LiVi-1n+12+DiVin+12+UiVi+1n+12=Bi    (5)

where L is the lower diagonal, D is the main diagonal, U is the upper diagonal, and B the right-hand side of the system defined in Equation 6.

Li=12πaiΔxπai−12RaΔxUi=12πaiΔxπai+12RaΔxDi=−(Li+Ui+2CmΔt+gtotn+12)Bi=2CmΔtVin+gNan+12ENa+gKdn+12EK+gMn+12EK+gTn+12ECa+gLn+12ECa+gLeakn+12ELeak  +gSynn+12Esyn+δi0Iinj(t)2πaΔx    (6)

with gNa, gKd, gM, gT, gL, gLeak, and gSyn representing the conductances for sodium, potassium, slow voltage-dependent potassium, high-threshold calcium, low-threshold calcium, leakage currents, and receptor-dependent synaptic conductance, respectively. gtot the sum of all the conductances. ENa, EK, ECa, ELeak, and ESyn the reversal potentials, respectively, for sodium ions, potassium ions, calcium ions, leakage, and receptor-dependent synaptic currents. Iinj the current injected, and δi0 the Kronecker delta.

The complete structure of the neuron corresponds to a tree of unbranched cables (sections) divided in N segments (or compartments), thus adding off-diagonal coefficients to the tridiagonal linear system (Hines, 1984) (Figures 2A, B). Through wise numbering of the nodes in the tree, the tridiagonal matrix resulting is solvable thanks to Hines matrix solver.

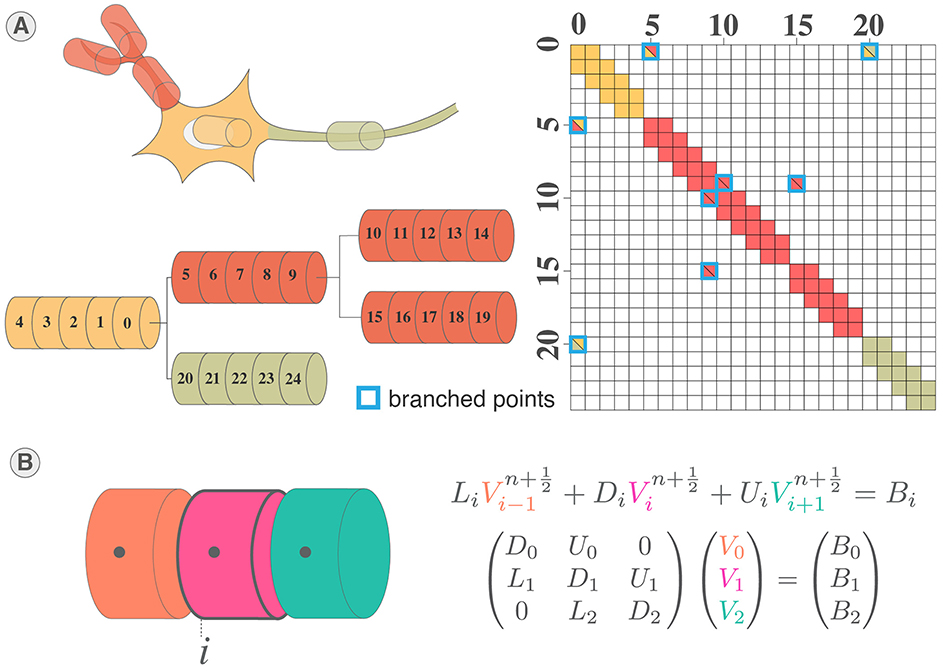
Figure 2. System of equations and solving of multicompartment model. (A) Illustration of mainly tridiagonal matrix with sparse coefficients (Hines matrix) at branches points generated by the multicompartmental neuron structure. (B) Illustration of the tridiagonal systems of equations corresponding to the computation of the membrane potential in a section of a multicompartmental neuron.

All the segments of neurons can be connected through fully configurable biomimetic synapses mimicking AMPA, NMDA, GABAA, and GABAB synaptic receptors (Destexhe et al., 1998) to allow fast and slow synaptic excitation or inhibition.

2.2 Computation core

The architecture of the pipelined computation core using 32-bit floating-point coding is presented in Figure 3.

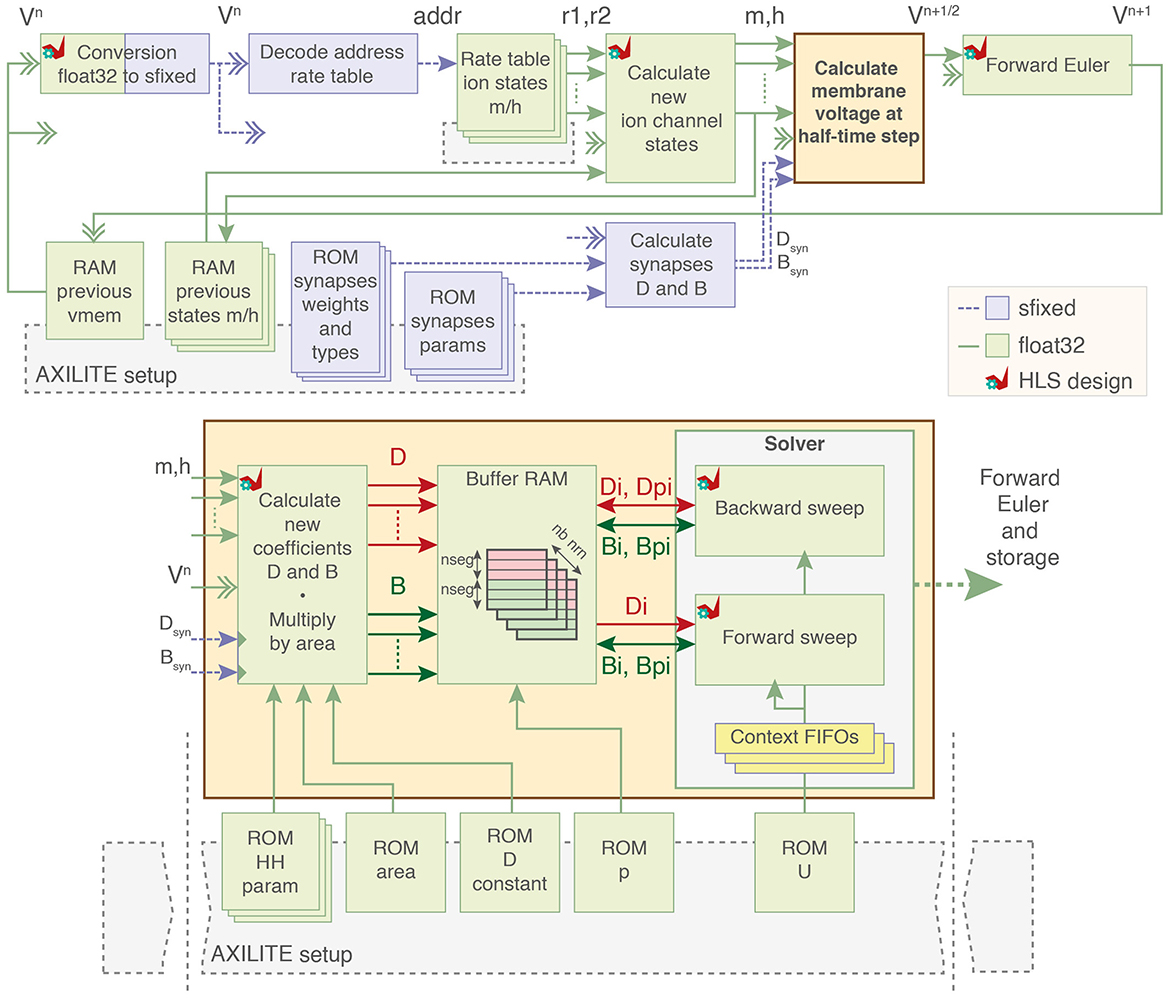
Figure 3. Block diagram of the computation core. Ion channel states variables are calculated from premultiplied rates and used to compute ion currents as two coefficients D and B. Dual-port buffer RAMs for D and B of each neuron load and store data to and from the forward and backward sweep cells. Parameters of the model are stored in block RAMs initialized by the PS through AXI-Lite. sfixed; signed fixed-point. float32; 32-bit floating-point. HLS, High-Level Synthesis using AMD Vitis HLS.

The computation core employs the Crank-Nicholson solver for its numerical stability and accuracy (Carnevale and Hines, 2006; Beaubois et al., 2022). Instead of relying on resource-intensive matrix inversion, a more efficient alternative is employed utilizing strategic compartment numbering and the Hines algorithm (Hines, 1984). Originally designed for CPU architecture, a variant of this algorithm utilized in the GPU-oriented simulator Arbor developed by the Human Brain Project community (Abi Akar et al., 2019) and in Valero-Lara et al. (2018) was implemented.

The algorithm uses a parent node vector p so the matrix can be stored using two vectors corresponding to the main diagonal D and upper diagonal U. Branching points are then reconstructed due to the parent node vector. Algorithm 1 solves the matrix, and Algorithm 2 generates the main diagonal D.

Algorithm 2. Initialize format main diagonal.

The computation of ion channel states is based on “premultiplied” HH rate function tables as described in Hines (1984), simplifying computation to a single multiply and add from table values looked-up based on the membrane voltage (Equation 7). This method eliminates the FPGA-specific limitations for complex mathematical functions such as division and exponential.

xn+1=r1(Vn)×xn+r2(Vn)    (7)

where xn+1 and xn are, respectively, the new and current value of the ion channel state, Vn is the membrane voltage at previous time step, and r1 and r2 are the ion rate tables decoded from the membrane voltage.

The premultiplied tables for common equations of ion channel states correspond to Equations 8, 9.

r1(V)=1-dt×(αx(V)+βx(V))r2(V)=dt×αx(V)    (8) r1(V)=1-dttaux(V)r2(V)=dt×x∞(V)taux(V)    (9)

where r1 and r2 are the pre-computed rate tables for ion channel states decoded from the membrane voltage, dt the time step in ms, and taux, x∞, αx, and βx the equations of the ion channel state depending on the formalism used.

The calculation module for synapses is adapted from BiœmuS (Beaubois et al., 2024) to match multicompartment equations allowing a fully configurable synaptic connection so all nodes can be connected and independently weighted. As for BiœmuS computed using 18-bit fixed-point coding, parameters of the synaptic models are set through AXI-Lite and pre-computed tables are used to encode the exponential rates of the synaptic receptors.

As the solving algorithm of the matrix includes sequential divisions and multiplications, the stability of the solving requires high accuracy that is better translated by floating point. Indeed, the coefficients greatly vary with the geometrical dimensions of the neurons that may create larger orders of magnitude that are delicate to handle with fixed point. Hence, 32-bit floating point was implemented to offer floating-point accuracy with limited resource consumption compared to 64-bit floating-point coding that shows significantly higher implementation cost in programmable logic for a limited gain in accuracy for this application.

The parameters of the model are loaded in BRAM through AXI-LITE registers controlled by the software application, hence facilitating interconnect of several cores thanks to AXI (Advanced eXtensible Interface) protocol. The AXI communications are clocked at 100 and 200 MHz, respectively, for ZynqMP and Versal architecture, while the rest of the design operates at 200 and 400 MHz, respectively, for ZynqMP and Versal architecture expect for the synapses that are clocked at 400 MHz for both architectures.

The computation core starts by loading the previous membrane voltage to decode the rate tables for ion channel states computation and allow computation in other modules. The computation of the values for ion currents is output as two separate coefficients D and B. The system solving includes two computation blocks that perform the backward and forward sweep of the Algorithm 1 along with context FIFOs to keep track on the solving state.

The coefficients for each segment are then stored in one dual-port RAM (lower addresses is D and upper addresses are B) with one BRAM per neuron. These BRAMs act as buffer memory for the operations of the forward and backward sweep by loading and storing the values of segments at each iteration until the matrix is completely solved.

Main computation modules were designed using High-Level Synthesis (HLS) through AMD Vitis HLS facilitating optimization, portability, and integration. Optimal HLS modules can be generated for each target and integrated easily in the design by adjusting the latency in the generic HDL.

A comparison with the NEURON software (Carnevale and Hines, 2006) has been conducted in prior work of the team (Beaubois et al., 2022) for the soma of a motor neuron including only sodium, potassium, and leak currents modeled using five segments of identical length, diameter, and properties. The emulation shows a slight difference with the NEURON software explained by the difference of solver that is CVODE for NEURON and Crank-Nicholson for the software emulation but mostly by the hardware architecture constraints in terms of data coding and operations. Indeed, the hardware is operating on 32-bit floating point by a FPGA instead of 64-bit floating point on software with a CPU for NEURON.

The selected architecture for the computation core designed is promoting the scaling in segments rather than neurons as the emphasized is put on the morphology of neurons better translated by a high number of segments. For example, the allocation of one BRAM per neuron allows for the storage of up to 576 segments per neuron.

2.3 Platform

The system corresponds to the integration of the computation core on SoC FPGA, specifically AMD Zynq UltraScale+ MPSoC and AMD Versal Adaptive SoCs, that can be organized in two parts: Programmable Logic (PL, i.e., FPGA) and processors in a Processing System (PS) part. The implementation on the low-cost System-on-Module (SOM) K26 (ZynqMPSoC architecture) embedded on either AMD Kria KR260 Robotics Starter Kit or Kria KV260 Robotics Starter Kit is capable of running up to 16 neurons of 64 compartments each with up to 1,048,576 fully configurable continuous conductance-based synapses. It includes on-board monitoring and offers external communication options such as Ethernet and expansion PMODs (standard peripheral module interface) allowing different compromises for monitoring and interconnection. Implementation on more performing architecture, such as AMD Versal Premium Series (VPK120 Evaluation Kit), increases the number of compartments to 96 segments each for an identical number of neurons using the same computation core.

The platform, allowing for emulation and monitoring as presented in Figure 4A, was developed using three different languages that correspond to three distinct parts as shown in Figure 4B.

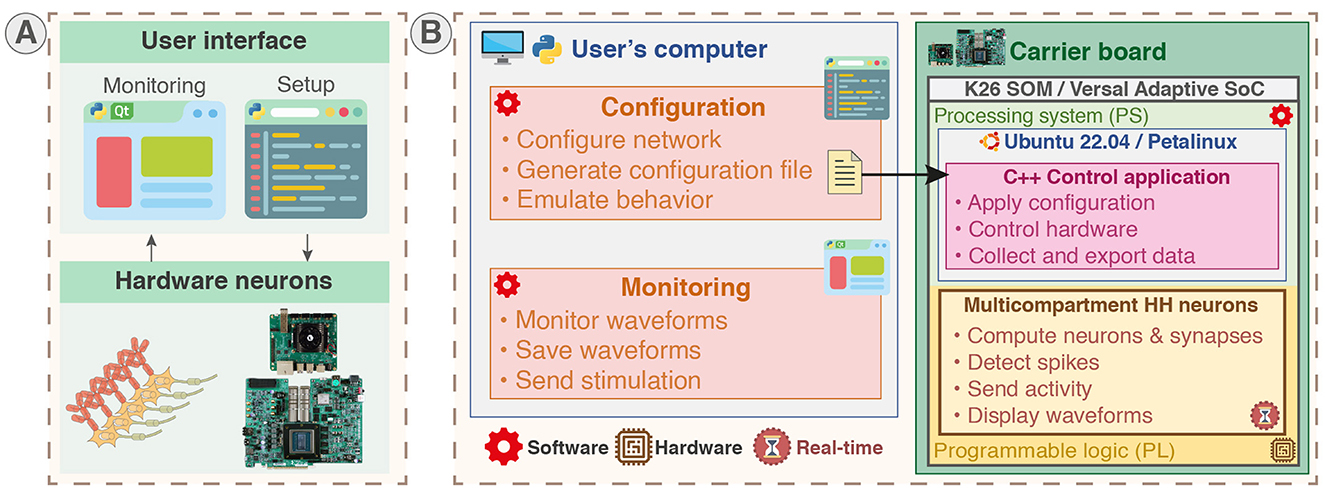
Figure 4. System overview of the real-time hardware-based emulator for multicompartment Hodgkin-Huxley neurons. The nature of each part of the system (software or hardware design) is identified by red and brown symbols. The on-board configuration and monitoring are also available but not displayed on the figure. (A) Overview of the platform integrating hardware neurons allowing users to configure and monitor the system through Python scripts and Qt-based GUI. The platform allows for real-time emulation of multicompartment Hodgkin-Huxley (HH) neurons with configurable parameters. (B) The system can run on carrier boards integrating different architecture of SoC featuring CPU in a processing system part (PS) and FPGA in a programmable logic part (PL), being either Zynq MPSoC through the System-on-Module K26 (SOM) or AMD Versal Adaptive SoC. The real-time hardware neurons are implemented in PL part and controlled through a C++ control application running in the PS part. The PS part runs either a Canonical Ubuntu or a custom Linux (generated using PetaLinux toolchain) allowing standard interfacing and operation. Monitoring is performed by a Qt-based GUI and setup by configuration scripts in Python ran either on-board or on another computer.

Python language is used for the configuration scripts and monitoring to provide user-friendly and rapid-prototyping as it is aimed to be used by non-specialists. The C++ language is used to develop the application responsible for setup and control in the PS part to provide better performances and proximity with hardware. VHDL was used to describe the hardware circuit in the PL part that implements the computation core of the neural network. Additionally, C++ code was used to generate the HLS IP used in the computation core. Figure 4B illustrates the different parts of the system and indicates their hardware or software nature for a configuration and monitoring on an external computer. The configuration of the network in Python can also be executed locally due to the operating system running in PS as shown in Figure 5A.

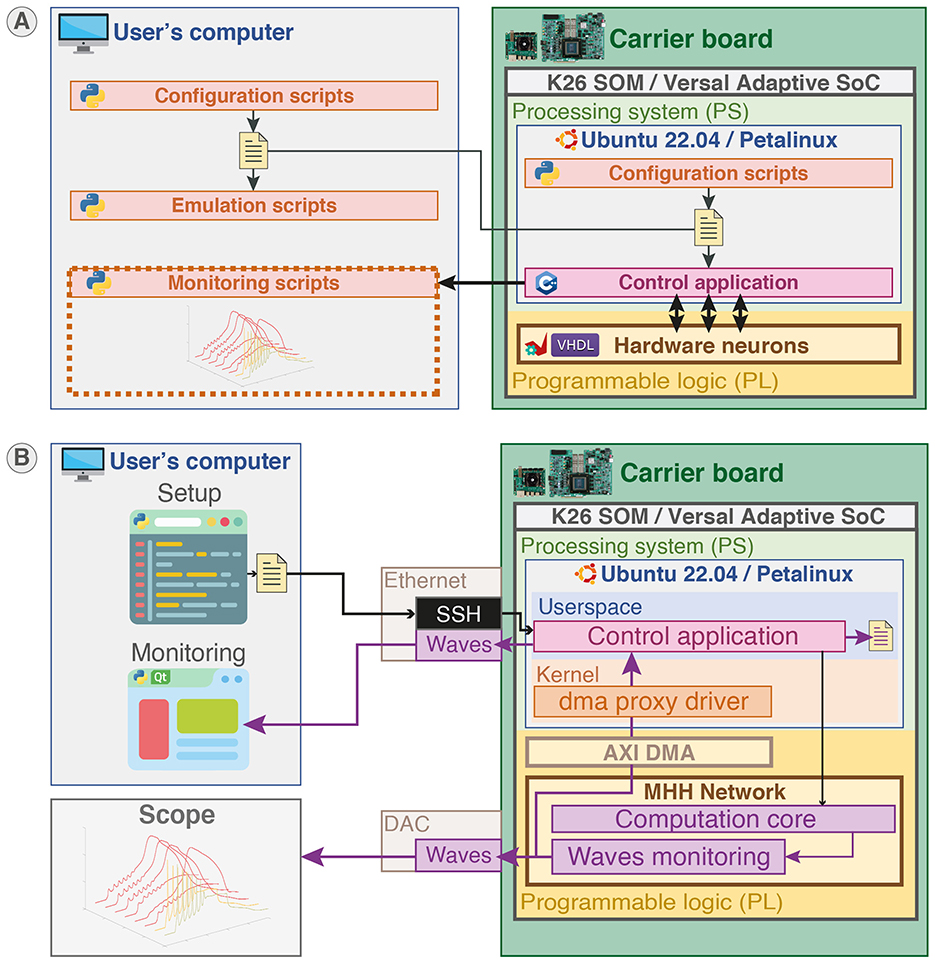
Figure 5. Platform configuration, control, and monitoring. (A) Platform configuration. Configuration scripts (Python) ran either locally or on another station generate configuration files. The configuration files are loaded by the control application (C++) running in the user space of the operating system (Canonical Ubuntu or custom Linux) in the PS part to set up the SNN in PL part. Emulation scripts allow emulation of the configuration beforehand to predict the behavior. (B) Platform control and monitoring. The platform can be controlled and monitored either remotely via SSH or on-board from the desktop through the control application. The membrane potentials of neurons can be monitored concurrently using Ethernet forwarding, on-board file saving, and visualization on scope by probing the Digital-to-Analog Converter (DAC).

All parameters of the HH model including the ion channels equations and geometrical properties are configurable from configuration scripts, enabling the emulation of various neuron types and morphologies, such as dendritic trees. Similarly, all parameters of the synapses are configurable via the configuration scripts, allowing for the emulation of various network topologies with great detail, due to fully configurable synapses that can connect