Synchronized stepwise control of firing and learning thresholds in a spiking randomly connected neural network toward hardware implementation

Since computing resources may be limited at the edge, we focus on analog spiking neural network (SNN) hardware having ultimately high-power efficiency for edge AI devices (Ning et al., 2015; Davies et al., 2018; Payvand et al., 2022). The most general neuron model for SNNs is the leaky integrate-and-fire (LIF) model (Holt and Koch, 1997). For a LIF neuron, IP function may be added by adjusting its time constant of the membrane potential Vmem according to its own firing rate Ffire . If we are to design LIF neurons with analog circuitry, tunable capacitor and resistor are required to control the time constant. The former is difficult because no practical device element having variable capacitance has been invented. For the latter, Payvand et al. (2022) proposed an IP circuit using memristors, namely, variable resistors. However, this circuit requires an auxiliary unit for memristor control, whose details are not yet discussed. Considering large device-to-device variability of memristors, each unit must be tuned according to the respective memristor’s characteristics, which would result in a complicated circuit system with large overhead (Payvand et al., 2020; Demirag et al., 2021; Moro et al., 2022; Payvand et al., 2023).

Alternative method for controlling Ffire is to adjust the firing threshold Vthr itself (Diehl and Cook, 2015; Zhang and Li, 2019; Zhang et al., 2021). For a LIF neuron designed with analog circuitry, Vthr is given as a reference voltage applied to a comparator connected to the neuron’s membrane capacitor (Chicca et al., 2014; Ning et al., 2015; Chicca and Indiveri, 2020; Payvand et al., 2022), hence IP can be implemented by adding a circuit that can change the reference voltage in accordance with Ffire . It would be straightforward to employ a variable voltage source, but we need a considerable effort to design such a compact voltage source as to be added to every neuron. Instead, we may prepare several fixed voltages and multiplex them to the comparator according to neuronal activity. This is the motivation of this study. What we are interested in are (i) whether or not stepwise control of the threshold voltage is effective for the IP function in a spiking RNN (SRNN) for temporal data learning and (ii) if it is, how far we can go in reducing the number of the voltage lines.

When we introduce variable Vthr , we need to care about SP for hardware design. With regard to SP implementation, spike-timing dependent plasticity (STDP; Legenstein et al., 2005; Ning et al., 2015; Srinivasan et al., 2017) is the most popular synaptic update rule. STDP is a comprehensive synaptic update rule that obeys Hebb’s law, but it is not hardware-friendly; it requires every synapse to have a mechanism to measure elapsed time from arrival of a spike. Alternatively, we employ spike-driven synaptic plasticity (SDSP; Brader et al., 2007; Mitra et al., 2009; Ning et al., 2015; Frenkel et al., 2019; Gurunathan and Iyer, 2020; Payvand et al., 2022; Frenkel et al., 2023) which is much more convenient for hardware implementation. It is a rule where an incoming spike change the synaptic weight depending on whether Vmem of the post-synaptic neuron is higher than a threshold VLthrUP or lower than another threshold VLthrDOWN .The magnitude relationship VLthrDOWN≤VLthrUP<Vthr is essential for correct learning hence VLthrDOWN and VLthrUP should be defined according to Vthr .

In this work we study an SRNN with IP and SP where Vthr , VLthrUP , and VLthrDown are discretized and synchronized. In order to make our model hardware-oriented, synaptic weights W are also discretized so that we can assume conventional digital memory circuits for storing weights. We perform simulations of learning and anomaly detection tasks for publicly available electrocardiograms (ECGs; Liu et al., 2013; Kiranyaz et al., 2016; Das et al., 2018; Amirshahi and Hashemi, 2019; Bauer et al., 2019; Wang et al., 2019) and show the effectiveness of our model. In particular, we discuss how much we can reduce the discretized levels of Vthr and W , which is an essential aspect for hardware implementation.

The neuron model we employ in this work is the LIF model (Holt and Koch, 1997), which is one of the best-known spiking neuron models due to its computational effectiveness and mathematical simplicity. The membrane potential Vmemi of neuron i is given as

where C , R , and Iin denote the membrane capacitance, resistance, and the sum of the input current flowing into the neuron, respectively. If Vmemi exceeds the firing threshold Vthri , neuron i fires and transfers a spike signal to the next neurons connected via a synapse. Then, neuron i resets Vmemi to Vreset and enters a refractory state for time tref , during which Vmemi stays at Vreset regardless of Iin . The LIF neuron is hardware-friendly because it can be implemented in analog circuits using industrially manufacturable complementary-metal-oxide-semiconductor (CMOS) devices (Indiveri et al., 2011), as illustrated in Figure 1A.

A synapse receives spikes from neurons and external input nodes. When a spike comes, a synapse converts the spike into a synaptic current Isyn proportional to W defined as

where τsyn and tspike are a time constant, and α is an appropriately defined constant. This synapse model is also compatible with the CMOS design.

As mentioned above, we employ SDSP as the synaptic update rule for SP. The synaptic weight Wij between pre-synaptic neuron i and post-synaptic neuron j increases or decreases if Vmemj is higher or lower than the learning threshold VLthrUPj or VLthrDOWNj when the pre-synaptic neuron i fires, as follows:

Wijnew=0.025V,0.05V,0.1V,0.3V, respectively. The ranges of W and Vthr are 0≤W≤2 and 0.125V≤Vthr≤0.4V . With regard to the SP synchronization with IP, we set VLthrUPi=VLthrDOWNi=Vthri/2 throughout this work, hence LRLthrUP = LRLthrDOWN=LRthr/2 . All initial synaptic weights between excitatory neurons are set to 1.0 , and the initial firing threshold is set to 0.2 V for all neurons. All other synaptic weights are set randomly. The validity of our method is though Counting Task Benchmark (Lazar et al., 2009; Payvand et al., 2022) as shown in Supplementary materials 4.1. 3.2 ECG anomaly detection

For ECG anomaly detection, we use the MIT-BIH arrhythmia database (PhysioNet, 1999; Goldberger et al., 2000; Moody and Mark, 2001). Using the PhysioBank ATM provided by PhysioNet (1999), we download and use MIT-BIT Long-Term ECG data No.14046 for performance evaluation. Figure 3A shows a part of normal waveform of the ECG used as training data. As test data, we use 10 hours waveform data of No.14046 that partially include multiple abnormal waveforms. Figure 3B shows a part of ECG waveform data used in the test. To perform anomaly detection, the SRNN is used as an inference machine. Values of the data points of the ECG waveform are inputted to the SRNN one by one in the time order. At the k -th input, it predicts the next k+1 -st. The firing frequency Foutk of the output-layer neuron at the k -th input is compared to the firing frequency of the input neuron at the k+1 -st input Fink+1 . Here, we define the abnormality judgment level Dthr to detect anomalies; if the absolute difference Dk+1=|Foutk−Fink+1|is greater than a predefined level Dthr , the k+1 -st input data is regarded to be abnormal.

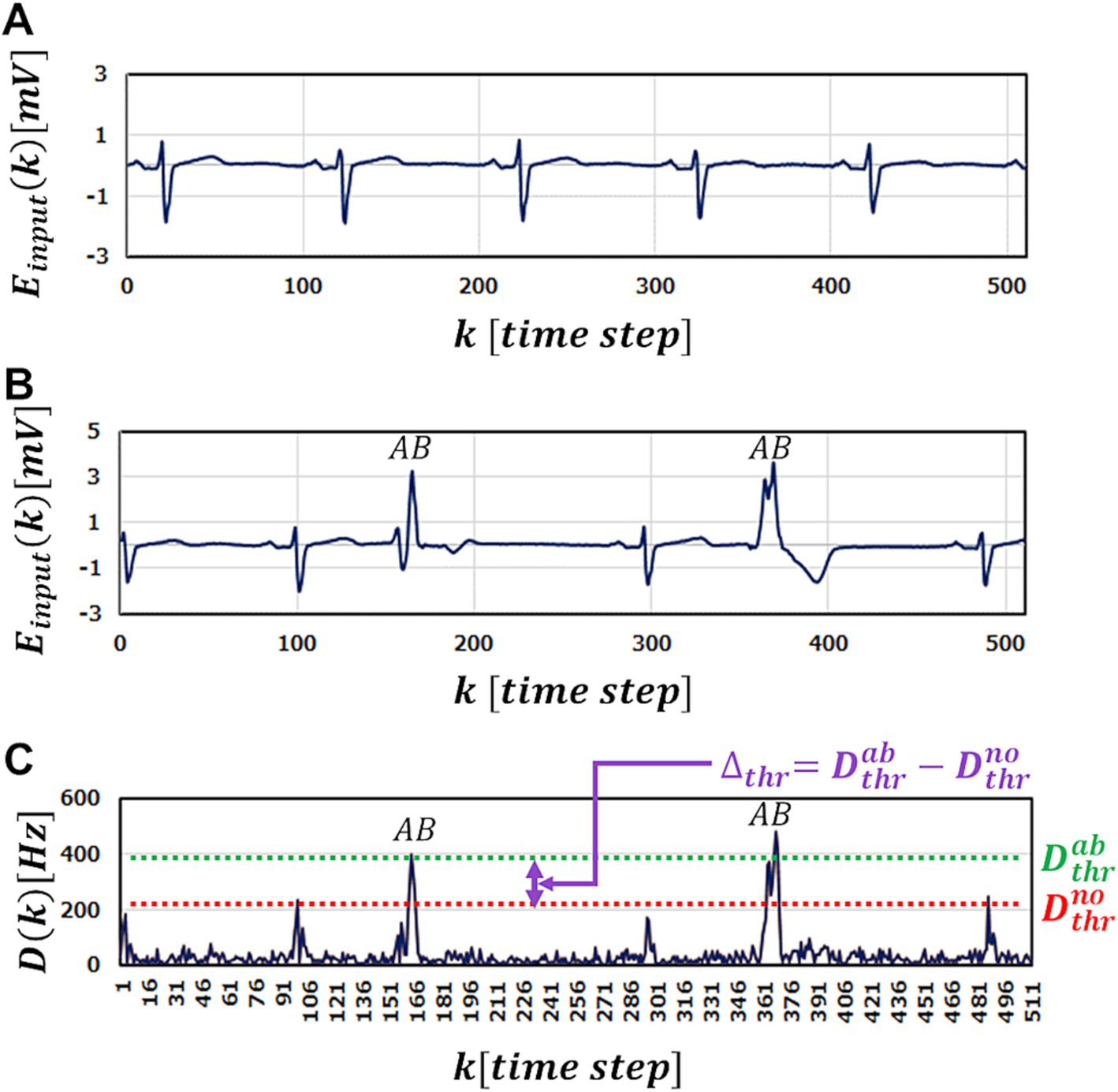
Figure 3. A part of ECG benchmark waveform No. 14046 used in the simulation. (A) A part of Normal ECG waveform used in training for M-SRNN. (B) A part of ECG waveform with abnormal points (labeled with AB). (C) The test results Dk of input (B).

Figure 3C shows the anomaly detection results Dk using M-SRNN reconstructed by our proposed method when the waveform data in Figure 3B is input. For highly accurate abnormality detection, Dthr must be set between Dthrno and Dthrab , where Dthrno is the highest peak of Dk for normal data input point, and Dthrab is the lowest peak of Dk for the abnormal points (Figure 3C). In other words, Dthrno is the smallest Dthr that does not misdetect normal data points, and Dthrab is the smallest Dthr that does not overlook any anomalies. Note that Dthrab is unknown in practical use; it is defined for discussion purpose. The window Δthr=Dthrab−Dthrno represents judgment margin, which should be large enough for correct detection without overlooking or misdetecting.

Since the raw ECG data Einput is given by time-series data of electrostatic potential in mV, the input-layer neurons convert the potential Einput to the firing frequency Fin as follows,

Fink=Fpoisson×4+2×Einputk5.

where Fpoisson is the conversion coefficient. Since an input-layer neuron fires with Poisson probability Fink , a single input is required to be kept for a certain duration ( Tbin ) to generate a desired Poisson spike train.

3.3 Simulation results 3.3.1 Effectiveness of proposed method on anomaly detection

Anomaly detection results of the initial M-SRNN and the M-SRNN reconstructed with both SP and IP are shown in Figures 4A,B, respectively. For reconstruction of the M-SRNN, we use the waveform data from 0 to 10ms of ECG waveform No. 14046 which does not include anomalies. The blue and orange line represent the probability of detecting an abnormal point as abnormal (true positive rate, TPR) and the probability of misdetecting a normal point (false positive rate, FPR) at each Dthr , respectively. These probabilities are obtained statistically from the 10 h data of No. 14064. As shown in Figure 4A, the initial M-SRNN cannot detect anomalies correctly because Δthr is negative; the misdetection rate (orange) is always larger than the correct detection rate (blue) at any Dthr . On the other hand, since Δthr is positive, the reconstructed M-SRNN can correctly detect anomalies (Figure 4B). Indeed, if Dthr is selected between Δthr , the 100% accuracy of the anomaly detection can be achieved while the misdetection rate is suppressed to 0% . Figures 4C,D show Receiver Operating Characteristic (ROC) curves of the initial M-SRNN and the reconstructed M-SRNN, respectively. Since Δthr<0 in the case of the initial M-SRNN, the ideal condition for anomaly detection, TPR = 1.0 and FPR = 0.0, cannot be achieved (Figure 4C). On the other hand, such condition is realized in the case of the reconstructed M-SRNN because Δthr>0 (Figure 4D). Therefore, our proposed method for the M-SRNN reconstruction is effective for detecting abnormalities in periodic waveform data (in practical use of this method, Dthr may be defined as an arbitrary value slightly larger than Dthrno because the actual value of Dthrab hence Δthr is unknown). Note that the M-SRNN should be reconstructed for individual ECG data (in this case No. 14064). If we are to execute detection tasks for another data set, we need to reconstruct of the M-SRNN using a normal part of the target data set prior to the detection task.

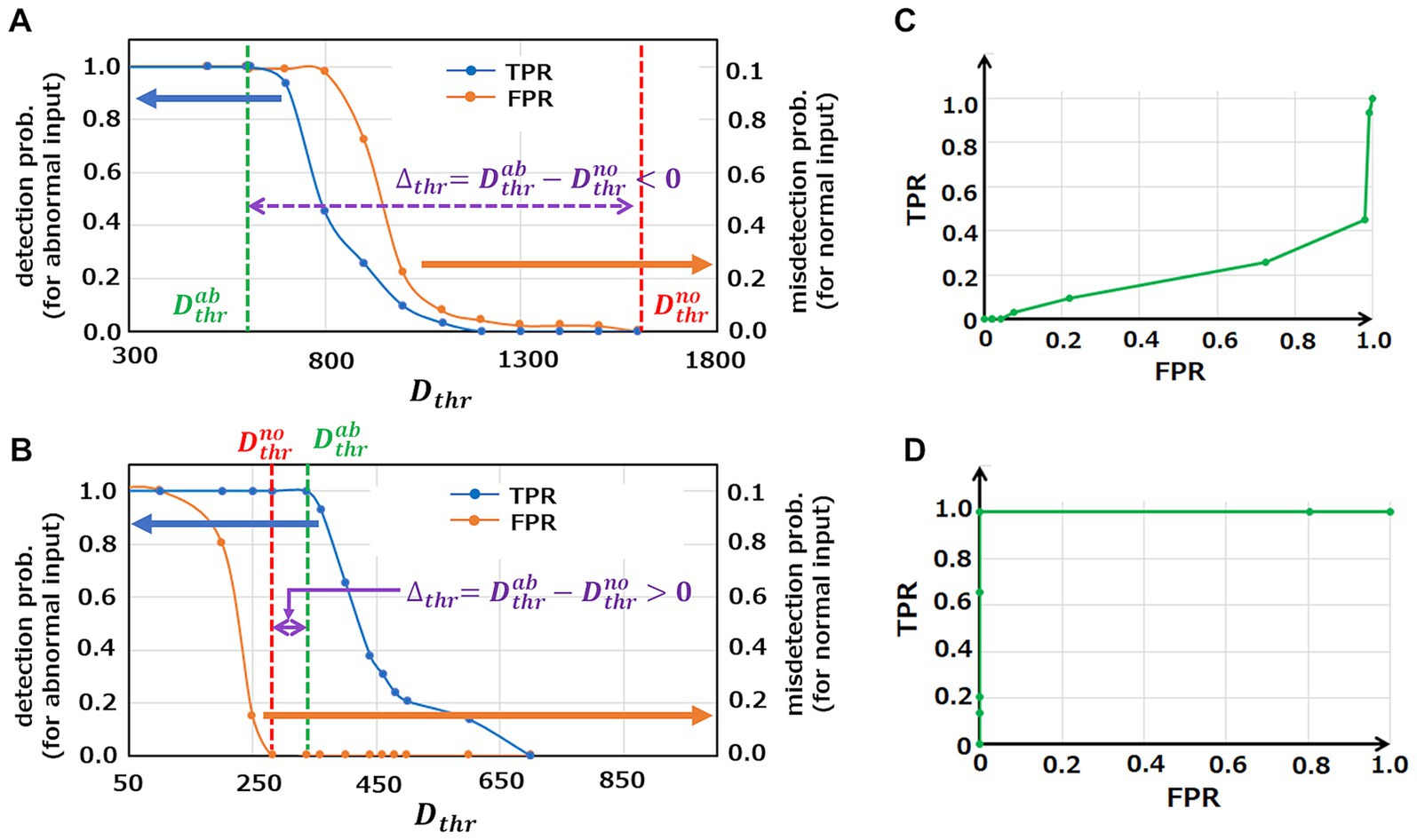
Figure 4. Analysis of anomaly detection capability in the case of using initial M-SRNN and reconstructed M-SRNN with Tbin=150ms , LRSDSP=2.0 , LRthr=0.025V , and σ=0.3 . (A,B) The probability of detecting an abnormal point as abnormal (TPR, blue) and the probability of misdetecting a normal point (FPR, orange) at each Dthr using initial M-SRNN and reconstructed M-SRNN, respectively. (C,D) ROC for initial M-SRNN and reconstructed M-SRNN, respectively.

3.3.2 Reduction of parameter resolutions toward hardware implementation

Figure 5 shows a heat map of Δthr at each LRSDSP∈SLR and LRthr∈Pthr when the processing time Tbin per one ECG data point for reconstruction is set to be 7ms (A), 150ms (B) and 600ms (C). These figures show that Δthr becomes large as the operation time Tbin increases, which is a reasonable result because the longer Tbin becomes, the more information is learned from the data point, leading to higher accuracy of the abnormal detection. In fact, as can be seen in Figure 6, which shows Dk patterns for an abnormal waveform obtained with the M-SRNN reconfigured by LRSDSP=0.1 and LRthr=0.3V for each Tbin , Dk becomes smoother and Dnomax lower as Tbin is set longer.

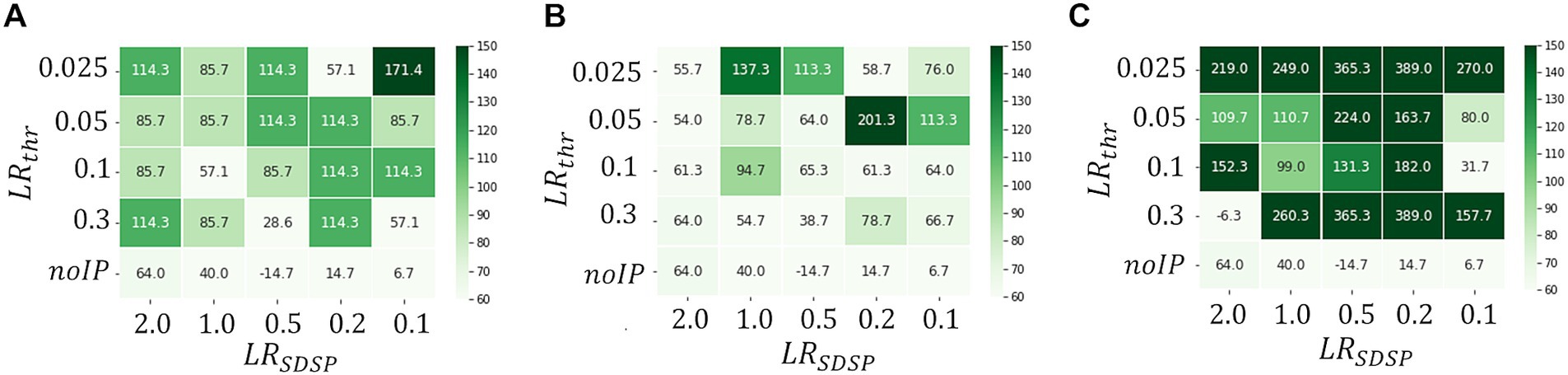
Figure 5. Heatmaps of Δthr . Tbin=A7ms,B150ms, and (C) 600ms , respectively. (ECG benchmark No. 14046).

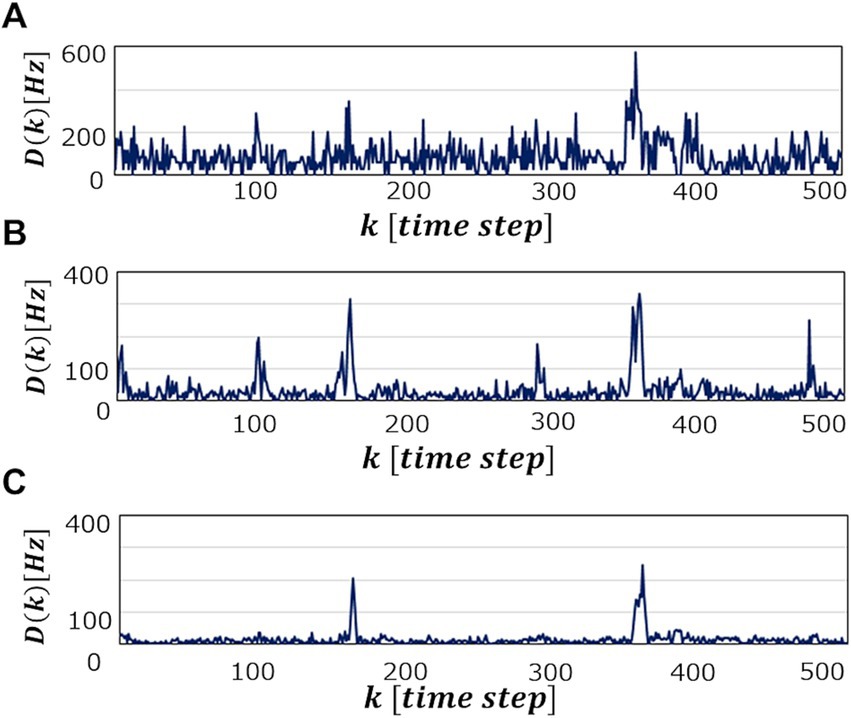
Figure 6. Dk when abnormal ECG waveform No. 14046 is detected in SRNN reconstructed with LRSDSP=0.1 and LRthr=0.3V . Tbin=A7ms,B150ms, and (C) 600ms , respectively.

3.3.3 Real-time operation for practical applications

For practical application, it is desired that the abnormal data should be detected at the moment it occurs and thus real-time operation is highly expected. In this sense, Tbin is desired to be as short as possible. In the case of the ECG anomaly detection, data is collected at 128 steps/s. Therefore, the learning process and anomaly detection must be performed within Tbin=7ms . However, as discussed above, such short Tbin leads to small Δthr because the learning duration for each data point is insufficient.

Now we assume that employing longer Tbin is equivalent to increasing the number of IP and SP operations within short Tbin . To increase the number of IP and SP operations, we have to enhance the activities of neurons, hence two options. The first one is to enhance the parallelism of the inputs; we increase the number of neurons in the input layer Ninput so that a neuron in the M-SRNN being connected to the input layer receive more spike signals during short Tbin . The other is to enhance the seriality of the input neuron signals; we increase the rate of Poisson spikes FPoisson from the input layer. The effects of these two methods are verified by simulation.

Figure 7 shows the heatmaps of Δthr for Tbin=7ms in the cases of Ninput=10 , 100 and 200 . We observe that Δthr increases with Ninput in general, indicating that our first idea is effective; real-time anomaly detection without false positive detection is possible by increasing Ninput . Note that the binary Vthr and W i.e., LRSDSP=2.0 and LRthr=0.3V result in sufficiently large Δthr even with Tbin=7ms in the case of Ninput=100 . Thus, a highly parallelized input layer has been shown to be effective for performance improvement with short Tbin . However, when Ninput is increased too much, the effect would be negative. As can be seen in Figure 7C, where Ninput=200 , the M-SRNN does not work appropriately when LRSDSP=2.0 and LRthr≥0.2V . Since the M-SRNN neurons that receive input spikes are always very close to the saturation in the case of large Ninput , precise control of the parameters such as Vthr and W is required.

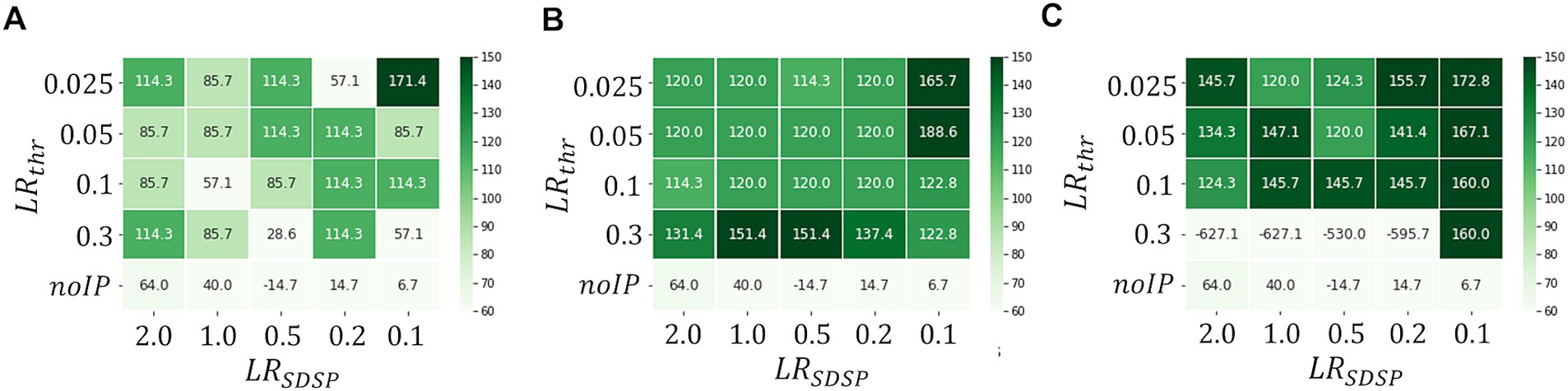
Figure 7. Heatmaps of Δthr in case of Ninput=A10,B100,andC200 ( Tbin=7ms ), respectively. (ECG benchmark No. 14046).

To examine the latter idea, we perform the anomaly detection tasks with FPoisson being varied. In the center of Figure 8, we plot obtained Δthr as a function of FPoisson . If increasing FPoisson does not play an effective role on performance improvement, Δthr increases just linearly with FPoisson , as indicated by a red dotted line. As a matter of the fact, however, we obtain Δthr above the red line up to FPoisson=1200Hz , indicating that raising FPoisson improves the anomaly detection performance of an M-SRNN.

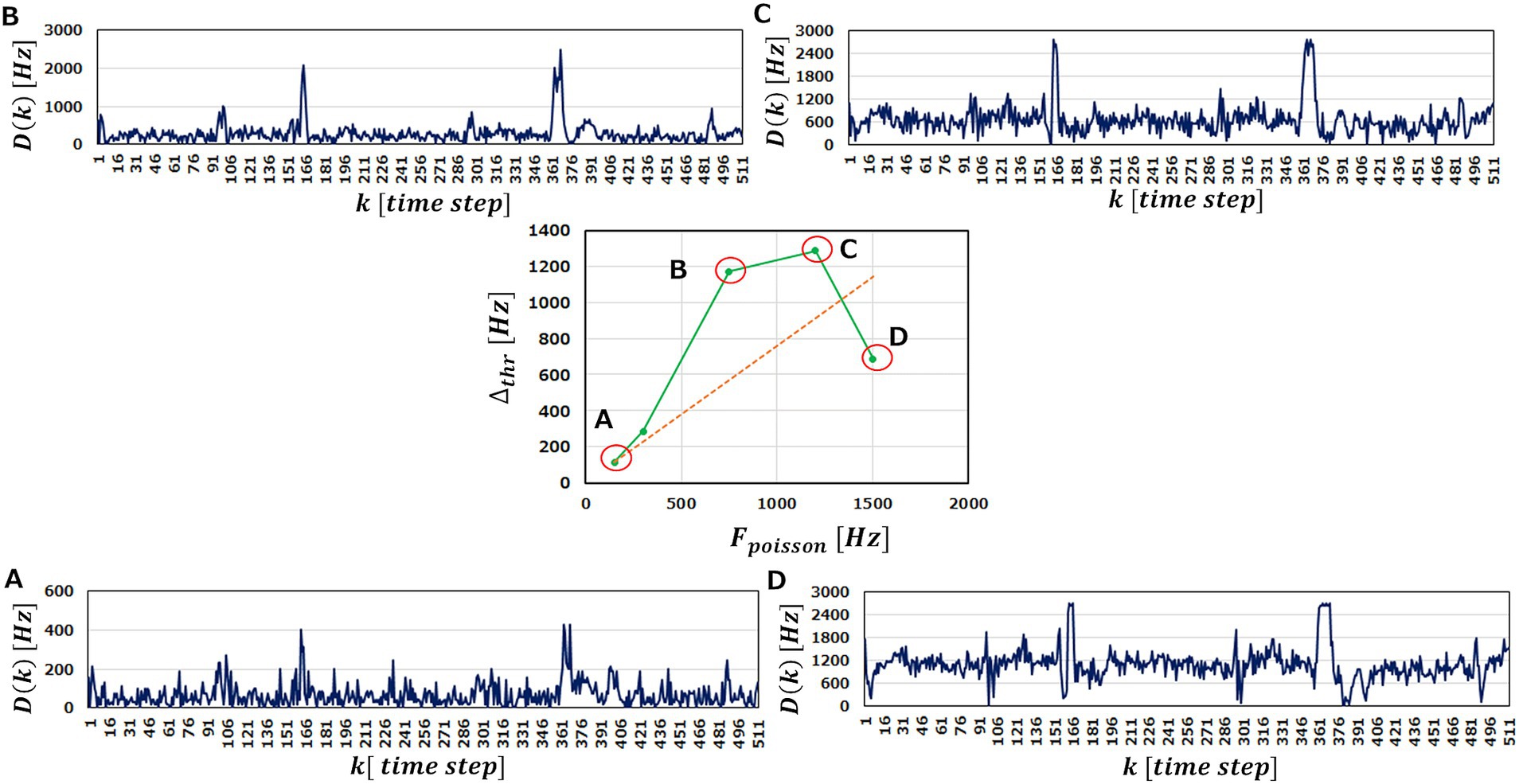
Figure 8. Δthr and Dk in the case of LRSDSP=2.0 and LRthr=0.3V . The center graph shows the Δthr against Fpoisson . The outer diagrams represent Dk corresponding to (A–D) points in the center diagram. Fpoisson=A150,B750,C1200 , and (D) 1500Hz , respectively. (ECG benchmark No. 14046).

We observe in Figures 8A–C that increasing FPoisson elevates the base line of Dk and magnify the peaks. This is reasonable because the more input spikes come, the more frequently the neurons in the M-SRNN fire, hence Dk being scaled with FPoisson . At the same time, it smoothens variation of Dk , indicating improved learning performance due to the increased IP and SP operations. This results in Δthr being larger than the red dotted line. When FPoisson is increased further to 1500Hz , the peaks corresponding to the abnormal data in the original waveform saturate, as can be seen in Figure 8D. This is because of the refractory time of neurons. Since a neuron cannot fire faster than its refractory time, it has an upper limit in its firing frequency. The saturation observed in Figure 8D is interpreted as a case where the firing frequency at the anomaly data points reaches its limit. As a result, Δthr at Fpoisson=1500Hz is suppressed and comes below the red dotted line. This discussion can be clearly seen in Figure 9, which shows the evolutions of Dthrno and Dthrab with Fpoisson of the input neurons. We observe that Dnomax increases linearly, while Dthrab increases only up to Fpoisson=1200Hz. For Fpoisson≥1200Hz , Dthrab reaches its limit and only Dthrno increases, hence smaller Δthr . We note that the results shown in Figure 8 are obtained with LRSDSP=2.0 and LRthr=0.3V i.e., binarized Vthr and W .

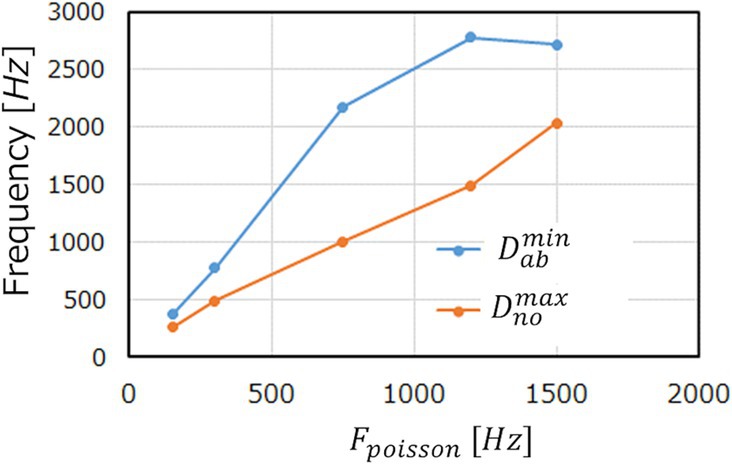
Figure 9. Dthrab and Dthrno with LRSDSP=2.0 and LRthr=0.3V against Fpoisson . (ECG benchmark No. 14046).

It is noteworthy that we have found that binary Vthr and W may be employed if the input layer is optimized. This is highly advantageous for hardware implementation. For Vthr (and also for VLthrUP/Down ), we may prepare the smallest 2-input multiplexers and only two voltage lines (see Supplementary materials). What is more conspicuous is that W can be reduced to binary. This means that for synapses we have no need of using an area-hungry multi-bit SRAM array or waiting for analog emerging memories, but we may employ just small 1-bit latches (see Supplementary materials). Since the number of synapses scales with square of the number of neurons, this result has a large impact on the SRNN chip size.

Thus, optimization of the input gives a large impact on both performance and physical chip size of the SRNN. Whether we optimize Niput or FPoisson may be up to engineering convenience. It is possible to optimize both. As we have seen in Figures 7, 8, the former has a better smoothing effect in the normal data area than the latter. Considering hardware implementation, on the other hand, the latter is more favorable because the former requires physical extension of the input layer system. For the latter, we only have to tune the conversion rate of raw input data to spike trains, which may be done externally. Therefore, the parameters in the input layer should be designed carefully taking those conditions discussed above into consideration.

4 Discussion

Lazer et al. proposed to introduce two plasticity mechanisms, SP and IP, to an RNN to reconstruct its network structure in the training phase (Lazar et al., 2009). While software implementation of SP and IP seems to be quite simple, we need some effort for hardware implementation.

With regard to the IP operation, Lazer et al. adjusted the firing threshold of each neuron according to its firing rate at every time step. In hardware implementation, constantly controlling the thresholds of all of the N neurons is not realistic. Therefore, we proposed a mechanism that regulate the threshold of a neuron in an event-driven way; each neuron changes its firing threshold when it fires in accordance with its activity being higher or lower than the predetermined levels. This event-driven mechanism releases us from designing a circuit for precise control of the thresholds. As discussed by Lazar et al., we need to control the thresholds with an accuracy of 1/1000 if it is done constantly, which requires quite large hardware resource that consumes power as well. Our event-driven method, on the other hand, has been shown to allow us stepwise control of the thresholds with only a few gradations, which is highly advantageous for hardware implementation.

Another way to realize the IP mechanism is to regulate the current of a LIF neuron (Holt and Koch, 1997). The current value can be adjusted by changing the resistance values in the previous researches (Dalgaty et al., 2019; Zhang et al., 2021). This can be achieved by using variable resistors such as memristors (Dalgaty et al., 2019; Payvand et al., 2022) or by selecting several fixed resistors prepared in advance. For the former method, precise control of the resistance would be a central technical issue, but it is still a big challenge even today because the current memristor has large variation (Dalgaty et al., 2019). Payvand et al. discussed that variation and stochasticity of rewriting may lead to better performance, but further studies including practical hardware implementation and general verification are yet to be done. The latter requires a set of large resistors (~ 100MΩ ) for each neuron, which is not favorable for hardware implementation because resistors occupy quite large chip area. We believe that stepwise change of the firing threshold is the most favorable implementation of IP.

For implementation of the SP mechanism, STDP (Legenstein et al., 2005; Ning et al., 2015; Srinivasan et al., 2017) is widely known as a biologically plausible synaptic update rule, but it is not hardware friendly as discussed in the introduction. Hence recent neuromorphic chips tend to employ SDSP (Brader et al., 2007; Mitra et al., 2009; Ning et al., 2015; Frenkel et al., 2019; Gurunathan and Iyer, 2020; Payvand et al., 2022; Frenkel et al., 2023). However, SDSP cannot be implemented concurrently with threshold-controlled IP in its original form, because the latter may push down the upper limit of the membrane potential (i.e., the firing threshold) below the synaptic potentiation threshold. Our proposal that the synaptic update thresholds synchronize with the firing threshold realized the concurrent implementation of the two, and their interplay with each other led to successful learning and anomaly detection of ECG benchmark data (PhysioNet, 1999; Goldberger et al., 2000; Moody and Mark, 2001) even with binary thresholds and weights if the parallelism and the seriality of the input are well optimized. This is highly advantageous for analog circuitry implementation from the viewpoints of circuit complexity and size.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://physionet.org/content/ltdb/1.0.0/.

Author contributions

KN: Conceptualization, Formal analysis, Methodology, Visualization, Writing – original draft. YN: Conceptualization, Formal analysis, Methodology, Supervision, Validation, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

KN and YN were employed by Toshiba Corporation.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnins.2024.1402646/full#supplementary-material

References

Ambrogio, S., Ciocchini, N., Laudato, M., Milo, V., Pirovano, A., Fantini, P., et al. (2016). Unsupervised learning by spike timing dependent plasticity in phase change memory (pcm) synapses. Front. Neurosci. 10:56. doi: 10.3389/fnins.2016.00056

PubMed Abstract | Crossref Full Text | Google Scholar

Ambrogio, S., Narayanan, P., Tsai, H., Shelby, R. M., Boybat, I., Nolfo, C., et al. (2018). Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558, 60–67. doi: 10.1038/s41586-018-0180-5

PubMed Abstract | Crossref Full Text | Google Scholar

Amirshahi, A., and Hashemi, M. (2019). ECG classification algorithm based on STDP and R-STDP neural networks for real-time monitoring on ultra low-power personal wearable devices. IEEE Trans. Biomed. Circ. Syst. 13, 1483–1493. doi: 10.1109/TBCAS.2019.2948920

PubMed Abstract | Crossref Full Text | Google Scholar

Bartolozzi, C., Nikolayeva, O., and Indiveri, G. (2008). “Implementing homeostatic plasticity in VLSI networks of spiking neurons.” in Proc. of 15th IEEE International Conference on Electronics, Circuits and Systems. pp. 682–685.

Google Scholar

Bauer, F. C., Muir, D. R., and Indiveri, G. (2019). Real-time ultra-low power ECG anomaly detection using an event-driven neuromorphic processor. IEEE Trans. Biomed. Circ. Syst. 13, 1575–1582. doi: 10.1109/TBCAS.2019.2953001