Cancer cell growth is a fundamental biological process characterized by cell proliferation, and an increase in cellular mass typically occurs under stress conditions. This complex process is strictly regulated and relies on vital nutrients like lipids and nucleic acids to provide sufficient energy to synthesize new cellular components. Particularly, cells have developed and improved their mechanisms for survival, allowing them to grow and develop in harsh conditions, which include reduced oxygen levels, inadequate availability of nutrients, and limited energy supplies (Semenza, 2003). However, Hypoxia-Inducible Factor-1 (HIF-1) is a transcription factor widely distributed and expressed in multiple organs in both animal and human organisms. It is crucial in coordinating many physiological reactions to hypoxic circumstances, such as initiating glycolysis to reduce oxygen deprivation and facilitating angiogenesis (Yang et al., 2021). Moreover, the HIF-1 is a central coordinator of many extracellular and intracellular signals associated with cellular proliferation and impacts metabolic control. The multidimensional nature of this entity makes it essential for both innate and adaptive immune responses, highlighting its huge influence on various cellular processes (Ruas et al., 2002).

Dysregulation of the HIF-1 pathway disrupts oxygen balance and growth homeostasis, leading to pathogenic conditions such as cancer, angiogenesis, and metabolic disorders (Semenza, 2010). To pharmacologically target HIF-1 for the therapy of related pathogenic diseases, it is necessary first to understand the coordinated dynamics of HIF-1 regulation (Semenza, 2003), (Boehme et al., 2021). Under hypoxic conditions, the interaction between energy deprivation and restricted nutrition availability occurs through complex mechanisms, impacting transcriptional and post-translational processes at various levels. The changes in gene expression facilitated by HIF-1 initiate disruption in the oxidative metabolism of mitochondria, glucose intake, energy production, and angiogenesis triggering. This process promotes cancer cell migration, survival, and multiplication (et Nurbubu, 2020).

Furthermore, the insulin and Glucagon ratio is important for glucose homeostasis. Low glucose levels under different physiological conditions produced by food intake or stress tumor microenvironments such as oxygen deficiency and inflammation release glucagon from the pancreas to increase blood glucose levels (Melillo, 2006). However, within the domain of cellular signaling pathways, a deficiency in oxygen and essential nutrients can lead to increased levels of reactive oxygen species (ROS). The increase in ROS levels results in the occurrence of oxidative stress, consequently disrupting many signaling pathways (Boehme et al., 2021), (Panieri and Santoro, 2016). It is important to highlight that the actions of HIF-1 and Glucose transporter-1(GLUT-1), which are affected by many types of reactive oxygen species (ROS), give rise to several intracellular effects that facilitate the growth and spread of cancer cells in situations that involve oxidative stress, limited nutritional availability, and energy insufficiency (Nagy et al., 2019).

The complex relationships between HIF-1, O-glycosylation transferase (OGT), Vascular endothelial growth factor (VEGF), and protein kinase B (AKT) are crucial because they all work together to control the expression of several enzymes involved in glucose and fatty acid metabolism as well as the regulation of glucose transporters during the start and development of cancer (Panieri and Santoro, 2016). However, precise metabolic regulation and the best possible functioning of the Mitogen-activated protein kinases (MAPK), AMP-activated protein kinase (AMPK), and AKT/PI3K pathways are necessary to maintain glucose homeostasis, which makes them desirable targets for therapeutic intervention (Jin et al., 2020), (Lee et al., 2019). In this context, HIF-1 plays a crucial role in allowing cells to adapt to hypoxic conditions by coordinating the expression of genes involved in critical processes such as angiogenesis and glucose metabolism via key cancer-related signaling pathways. HIF-1 can promote its cancer-related actions by either acting as a facilitator of oncogenic processes or modulating downstream targets within tumor-promoting signaling pathways (Huang and Zhou, 2020). Although the role of HIF-1 in cancer is well-known, there remains a lack of comprehensive investigation into its connections with important variables such as VEGF, GLUT-1, and OGT within the framework of epigenetic mechanisms, along with other crucial entities such Extracellular single regulated kinase (ERK), β-catenin, p53, AKT, and C-MYC. A thorough examination of these factors is necessary to gain a comprehensive understanding of how they collectively induce the activation of HIF-1 and promote the metastatic progression of cancer.

Prior studies have examined the therapeutic potential of HIF-1 using in vivo and computational analyses (Huang and Zhou, 2020), (Poon et al., 2009), (Onnis et al., 2009). However, more research is still needed into their impact on downstream target genes, such as GLUT-1 and the crucially related signaling networks. Consequently, to shed light on the epigenetic regulation of GLUT-1, a crucial component in the initiation and spread of cancer, our research focuses on constructing a Boolean Regulatory Network (BRN) model for HIF-1 signaling. In order to accomplish this objective, we implemented a qualitative modelling methodology that relied on the René Thomas formalism (Thieffry and Thomas, 1995). The wet laboratory data was employed in our study, which was represented using computation tree logic (CTL) to estimate parameters. Additionally, we implemented the model verification technique, as depicted in Figure 1. The primary objective of our comprehensive examination of the model trajectories was to clarify the interconnected pathways associated with the increased expression of HIF-1, the initiation of the oncogene C-MYC, and the suppression of the tumor suppressor gene p53. These elements collectively lead to either the progression or recovery of cancer invasion and homeostasis.

Figure 1. This workflow demonstrates the comprehensive research methodology employed in this study. Step 1: Represents the extraction of the knowledge driven HIF-1 signaling pathways from KEGG database and creating interaction graphs from experimental data to construct a BRN by using reduction rules. Step 2: Computation Tree Logic (CTL) formula is generated based on experimental data and parameters are assigned using SMBioNet, it uses NuSMV for model checking to verify the experimental observation in (Supplementary Material S1). Step 3: Shows the methodology steps for the dynamics simulation of the BRN using the GINSim tool, generating state graphs for the analysis of normal and pathogenic conditions. The resulting state graphs are visualized in Cytoscape, emphasizing the maximum betweenness centrality of states to analyze and identify crucial trajectories, cycles and deadlock states. Step 4: Represents the flow chart of concentration analysis of finally selected entities in SimBiology using Matlab.

The research method employed in this study is visually shown in Figure 1. It describes the procedures followed to complete the study and get the results.

In this study, we employ a mathematical framework called the kinetic logical formalism, initially developed by Rene Thomas and refined in prior research on modelling biological regulatory networks (BRNs) (Thieffry and Thomas, 1995). To conduct our modelling, we use the GINsim utility, as described in (Ahmad et al., 2012). However, positive and negative feedback loops are two essential feedback mechanisms in BRNs that kinetic modeling considers and incorporates. The activation of different components within the network is enhanced by positive feedback processes, which are essential in producing several stable states. Conversely, negative feedback mechanisms prevent various components from acting independently and are essential for generating oscillatory behavior or preserving homeostasis, the state of stability within a system (Thomas et al., 1981). Several studies have investigated genetic networks, focusing on formal methods for analyzing positive and negative feedback loops, as first described by (Thieffry and Thomas, 1995).

In qualitative models, the state space of these models grows exponentially with the number of components. A reduction approach has been created to tackle this problem; it seeks to reduce the size of qualitative models while maintaining their structural and dynamic properties. A signaling route is depicted in Figure 2 that has been reduced to produce a Boolean Regulatory Network (BRN) (Cui et al., 2010), (Saeed et al., 2016), as shown in Figure 3. The reduction procedure was carried out by implementing particular reduction rules comprehensively defined in prior research studies (Saadatpour and Methods, 2023), (Naldi et al., 2010). These reduction principles have been used to simplify complex signaling pathways like mTOR, PI3k, and AKT, ultimately creating BRNs that can include any possible regulatory feedback circuits (Saeed et al., 2016).

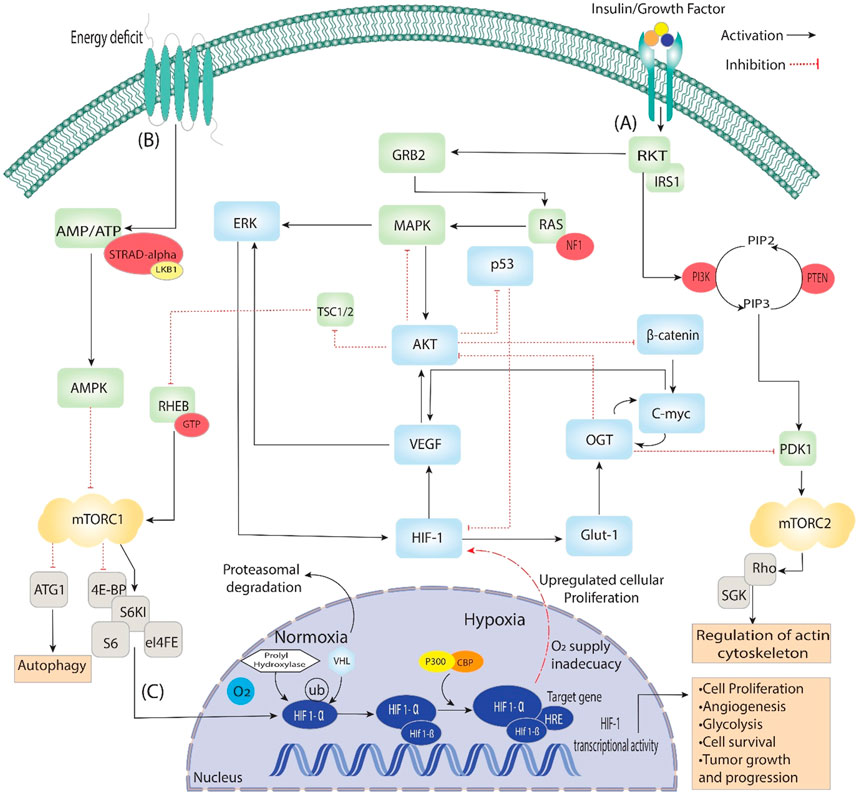
Figure 2. Activating insulin growth factors and energy deprivation triggers the HIF signaling pathway. It is divided into three steps: (A) When insulin binds with the epidermal growth factor, it starts signal transduction through auto-phosphorylation. It phosphorylates the ongoing genes RKT, GRB2, IRS1 and PI3k, which converts PIP2 to PIP3, then phosphorylation of PDK1. Additionally, PDK1 phosphorylates mTORC2, which is involved in regulating actin cytoskeleton. On the other hand, GRB2 phosphorylates RAS and activates the MAPK signaling pathway, which starts the phosphorylation of AKT and ERK, directly involved in Angiogenesis through VEGF and HIF-1. Furthermore, AKT is a central pathway regulator that inhibits β-catenin, p53 and TSC1/2, which dephosphorylate RHEB and, through GTPase, activate mTORC1. (B) During the energy deficit condition, the AMP/ATP ratio is maintained through AMPK, which dephosphorylates the mTORC1 and is involved in the process of autophagy and activates HIFs. (C) In the nucleus, HIF-1 stabilizes, binds VHL/PHD HIF1-α and reaches the target gene with the help of P300, which acts as a coactivator. The HIF-1α/HIF-1β complex binds to the HRE region of the target gene, triggering the hypoxia response and activating various up-signaling genes, including VEGF and GLUT-1, and they activate associated genes.

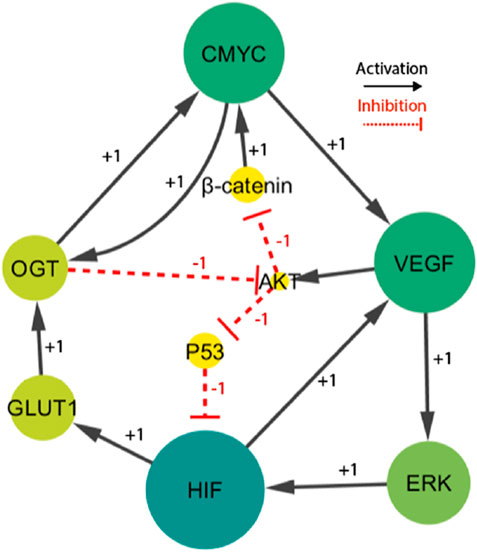
Figure 3. The HIF- one linked BRN reduces the signaling cascade highlighted in Figure 1. Particularly, the sign “+1”indicates a positive (activating) interaction, while the sign '-1′ indicates a negative (inhibiting) interaction.

This section provides a brief description of the formal semantics that have been embedded into Rene Thomas' framework (Bernot et al., 2007). The framework presented in this study serves as a foundational theoretical basis for understanding the precise mathematical constructs and principles that govern the intricate dynamics and interactions of components within complex systems. Its application is particularly focused on the domain of biological regulatory networks. The framework developed by Thomas offers a systematic and precisely specified approach for identifying and studying the dynamic behaviors shown by these systems. As a result, it serves as a fundamental basis upon which further research and modelling efforts are constructed.

Biological Regulatory Networks(BRNs), defined as complex systems governing biological processes within living organisms, serve as systematic frameworks for formally representing biological interactions through directed graphs (G = (V, I)). In this representation, 'V' signifies the discrete nodes that comprise a biological system. The set I, which is a subset of V × V, serves to define the interactions between entities, indicating the entities that produce impact on others. Every biological entity inside the network possesses both successors (G+vi) and predecessors (G−vi) (Bernot et al., 2007).

In this system, every node referred to as an entity is allocated a parameter denoted as ℓvi, which is dependent on the count of its successors. When an entity possesses one or more successors, the value of ℓvi is equivalent to its number of successors. Conversely, if the entity has no successors, the value of ℓvi is equal to 1. Pairs represent the edges present in the network (τ, σ), where τ indicates the type of interaction, denoted by a positive symbol “+” for activation or a negative symbol “-” for inhibition. The influence threshold is defined as τ ≤ ℓvx, which is determined by the specific properties of the interaction τ (Bernot et al., 2007).

A biological regulatory network’s “state” refers to the particular configurations and degrees of expression of each biological component at any one time, providing information about the network’s dynamic behavior and reactions. This information is critical for understanding the network’s functionality as it responds to various stimuli and environmental changes. The provided information offers a concise representation of the behavior and interaction of the components inside the system, hence providing significant insights into its dynamic behavior.

The qualitative state of biological regulatory networks can be accurately characterized by the vector (E = ev1, ev2, …, evn), which provides a careful representation of the features of the network components. The comprehensive depiction facilitates understanding the network’s dynamics and adaptive reactions. Each component, evi, correctly denotes the level of expression of a given entity vi and is directly linked to the complete set Ivi. At its core, Evi functions as an abstract concept representing the intricate and situation-dependent expression of the biological entity vi in a certain condition (Bernot et al., 2004). The computation of the state space in a biological regulatory network is a crucial task logically achieved by applying Equation 1. This mathematical equation, similar to a Cartesian product, facilitates a systematic investigation of the extensive and complicated network, which contains huge possible combinations of entities at different expression levels.

The letter Z plays a vital role in this equation, representing the vast range of possible network states. It can only be calculated by systematically summing up the many levels of expression that define each entity. Importantly, it must be emphasized that the dynamic interactions with its predecessors intrinsically govern the vi expression level. The complex network of interdependencies among entities and their surrounding variables has a significant role in modeling the diverse range of possible states within the system, illustrating the intricate complexity commonly observed in biological systems.

In a biological regulatory network (BRN), represented as G = (V, I), an important concept is introduced: “resources.” The set Rvz is defined as the collection of particular elements vy that belong to the set G, except the element vz and the selection of these elements depends upon specific criteria. Specifically, if Evy is equal to or larger than a certain threshold τvy, vz, and a positive interaction exist shown by αvy, vz = “+,” these elements are chosen. Conversely, if Evy is less than the threshold τvy, vz, and αvy, vz = indicates a negative interaction “-,” these elements are selected. Rvz functions as a repository of resources, while vz symbolizes a variable belonging to the V set, with its state indicated as Evz. The existence of activators and the lack of inhibitors determine whether or not to treat entity “vi” as a resource. If vi has activators, it can be considered a component of Rvi. On the contrary, when inhibitors are present, they have a role in preventing vi creation. As Vi progresses along its evolutionary path toward its goal state, its expression level, represented by Kvi, is closely related to positive integers. These numbers are also known as logical parameters and are grouped under Rvi (Bernot et al., 2004).

The resource idea outlined above is crucial in understanding the complex relationships between nodes in a BRN. These interactions determine the presence or absence of particular activators and inhibitors in addition to the quantitative expression levels of these entities. The complex dynamics of the system are carefully controlled by logical parameters, which significantly impact the network’s behavior and ability to achieve specified regulatory results.

In the graphical representation of a BRN shown as G = (V, I), the state graph, denoted by E = (S, T), includes two important nodes (Bernot et al., 2004).

This part is a grouping of states, where each state is an arrangement of unique entities in the network. It essentially records the system’s configuration at a certain moment in time.

This relation describes how the system can change from one state to another and defines the relationship between states. This elucidates the dynamic nature of the network.

The transition relation (T) follows a certain condition: s⇒ s' ∈ T if the following requirements are satisfied.

• In a biological regulatory network, differences in the expression levels of two separate entities, called Evx and Evx', in different states (s and s'), are written as Evx = Evx △ Kx (Rvx).

• Expression levels in state s and state s' are the same for all other entities y ∈ V (apart from x), shown as Epy = Epy.

As a result of this description, we can see how the state graph is built and how changes in the expression levels of certain entities in the network determine transitions between states. The framework offers a systematic approach to understanding the network’s dynamic behavior and the factors that drive its transitions between various states.

The parameter selection in qualitative modeling of Thomas networks is significantly influenced by logical factors determining the system’s behavior that are initially unknown. The previously mentioned features or parameters play a crucial role in developing the system’s dynamic phenomena such as cycles, stable states and transitions, which are visually represented as a directed state graph (Bernot et al., 2004). The presented graph comprehensively represents significant phenomena to systematically identify and validate these parameters, by employing a formal model-checking approach using the tool SMBioNet, specifically designed to analyze such networks (Khalis et al., 2003). The SMBioNet tool enables the implementation of this method, which is intended to explore various states of the model and match parameters with experimental data ensuring both logical consistency and biological relevance. Parameters that are logically consistent are of utmost significance in qualitative modeling (Thieffry and Thomas, 1995).

In qualitative modeling, parameters do not take numerical values but are instead logical in nature, defining whether a biological entity, such as a gene or protein, is active, inhibited, or neutral. SMBioNet constructed based on qualitative formalism developed by Rene Thomas relies on two phases: the initial phase of the parameter derivation process involves formulating hypotheses based on biological data. This information is encapsulated in a CTL equation that defines temporal properties of biological entities like stability, oscillations and their network interactions, or specific sequences of activation and inhibition expected in biological systems (Baltazar et al., 2011). The second phase set of logical constraints derived from an iterative process to fine-tune the model parameters. These parameters are systematically modified to either satisfy the CTL formulae or match the observed biological behaviors, ensuring logical consistency across different states and conditions within the network (Thieffry and Thomas, 1995), (Baltazar et al., 2011).

However, we used model checking after this iterative change to confirm the settings. The chosen parameters created the intended qualitative characteristics, such as stable states or oscillating patterns, and were consistent with experimental data, SMBioNet thoroughly examined every state of the network (Khalis et al., 2003). The resulting model visually depicted these dynamic behaviors as a directed state graph, emphasizing important characteristics like stable states and cycles essential for comprehending the system’s dynamics.

In CTL quantifiers play a crucial role in expressing the properties and behaviors of systems. Quantifiers allow us to explain the existence or absence of certain states or paths inside a system’s state space. However, CTL utilizes a formula (zpi = n) to evaluate the current state. This formula determines whether the expression level of the variable pi precisely matches the required value n. This evaluation process facilitates the systematic analysis of dynamic behaviors in biological systems. The formulation of CTL formulae involves the combination of logical connectives with temporal operators. Within the context of logical connectives, the utilization of negation (“¬”), logical disjunction (“∨”), logical conjunction (“∧”), and implication (“⇒”) is prominent. In addition to this, we incorporate temporal operators that consist of pairs of symbols. In these combinations, the first element may take the form of an “A,” which would indicate the existence of all possible routes, or it could take the form of an “E,” which would indicate the existence of at least one path. After this, operators such as “X” are used to signify the subsequent state, “F” is used to denote any upcoming state, and “G” symbolizes all potential future states. In order to generate formal expressions that specify characteristics and behaviors within a system, the CTL quantifiers and operators are essential components. They provide the accurate and organized expression of system attributes and the need to perform analysis and verification (Bernot et al., 2004).

GINsim, a tool of significant value in biological modelling, is crucial in constructing state graphs that provide insights into two essential dynamics in biological systems. The same phenomenon can be observed through the qualitative cycle represented by the ordered pairs (0,0), (1,0), (1,1), and (0,1). This cycle is a typical reaction mechanism in biological systems to preserve homeostasis. On the other hand, as the state (2,1) illustrates, a qualitative situation may result in various actions, which could eventually lead to pathogenic effects or deadlock states. In particular, four distinct qualitative states collectively constitute a cyclic behavior: (0,0), (1,0), (1,1), and (0,1). These states are crucial in maintaining equilibrium and controlling dynamic processes, making them essential to comprehending the cyclic behavior seen in many biological systems (Schwab et al., 2020).

The development of state graphs, which are representations of the dynamic behaviors observed in biological systems, relies heavily on qualitative modelling methodologies. However, it becomes essential to adopt a systematic method when dealing with a state graph exhibiting higher complexity levels. The complex characteristics inherent in qualitative modelling can result in creating a comprehensive state graph, even when dealing with interaction networks of a relatively small scale. Moreover, the state graphs represent qualitative states using extended binary sequences. Due to the complex structure of these state graphs, conducting a manual analysis becomes difficult. Therefore, researchers frequently employ network analysis techniques based on graph theory to overcome the difficulty of choosing crucial trajectories within state graphs produced by qualitative modelling (Gonzalez et al., 2006). This methodology facilitates a more precise and effective analysis of the complex dynamics essential in biological systems.

Using graph-theoretic approaches has shown to be particularly efficient in examining extensive protein networks. Within the domain of graph connection, network analysis methodologies demonstrate proficiency in structuring the state graph by highlighting nodes according to their betweenness centrality rankings, ranging from the highest to the lowest values. States with high betweenness centralities are of great interest in biological phenomena. These states are more likely to arise and indicate factors that substantially impact numerous biological processes. Utilizing betweenness centrality measures allows for the assessment and differentiation of qualitative states, facilitating the identification of significant and influential paths within a certain cycle (U. B.-J. of mathematical sociology and undefined, 2001). Identifying crucial nodes within complex biological regulatory networks is essential for understanding cellular processes. Centrality, a commonly utilized measure derived from Social Network Analysis in graph-theoretic frameworks, is commonly applied to assign rankings to entities inside these complex networks (Kourtellis et al., 2013). Centrality analysis is a highly important method for identifying crucial aspects and characteristics of complex biological regulation networks. This technique provides insights into the key players and their interactions, enhancing our understanding of these networks.

In the framework of state graph analysis designated by “R” betweenness centrality appears as a key metric to assess the importance of particular qualitative states. In order to achieve a more thorough understanding of this concept, it is essential to examine it within the framework of three discrete qualitative states, namely, e1, e2, and e3. These states play a crucial role in comprehensively examining the phenomenon observed in biological systems, highlighting their dynamic behaviors and mechanisms that maintain equilibrium. When attempting to find the most efficient route between states e1 and e2, it is crucial to consider the total number of paths that pass through the intermediate state e3 (L. F.- Sociometry and undefined, 1977).

The betweenness centrality, written as BC(e3), is a quantitative measure that analyses the degree to which the state e3 serves as a bridge or intermediary relationship between other states within the network. The given statement quantifies the proportion of the shortest pathways that include e3 while examining all possible combinations of states between e1 and e2. However, the mathematical representation of e3 by calculating betweenness centrality is described in Equation 2:

The symbol σe1, e2(e3) is utilized to quantify the shortest pathways from the initial state s1 to the final state e2 while incorporating the intermediate state e3. It is an effective technique for comprehending and improving systems, especially in domains like network analysis and transportation of genes or entities. Meanwhile, the shortest routes connecting states e1 and e2 are represented by σe1, e2. All possible variations of e1, e2, and e3 states are included in the summing process. It is important to highlight that within the state graph of a biological system, every qualitative state corresponds to a distinct and possible pattern. However, it is important to emphasize that the edges of the state graph are commonly started in random order, which adds to the network’s behavior and structure complexity. This complexity highlights the significance of betweenness centrality to identify the central function of individual states in the larger network dynamics.

SimBiology, a computational modeling and simulation platform, was employed to investigate the dynamics of solute concentrations within the biological system under study. The model incorporated key biological entities, such as p53, AKT, β-catenin, VEGF, HIF-1, ERK, and GLUT-1, with their initial concentrations derived from literature and empirical data to reflect their typical levels in cancerous tissues. A detailed model of the system was constructed, incorporating the relevant biological processes and interactions. Initial concentrations of all solutes were specified, and the model was simulated over time. The simulated concentrations of various solutes were monitored and analyzed to gain insights into their behavior and the underlying mechanisms influencing their dynamics (David et al., 2015). The simulation was run over biologically relevant time units to capture both rapid signaling events and longer-term equilibrium states. Ordinary differential equations (ODEs) were used to define the interactions between these solutes, with rate constants representing their production, degradation, and feedback mechanisms. These constants were carefully chosen based on experimental data, ensuring the biological relevance of the interactions. Equilibrium concentrations were calculated to identify stable states in the system, and sensitivity analysis was conducted to ensure the robustness of the model, allowing for insights into how small changes in parameters could affect system behavior. Concentration versus time curves were plotted to visualize the changes in solute concentrations over time. Equilibrium concentrations were calculated to identify the stable state of the system. SimBiology built-in functions were utilized to assess concentration gradients, fluxes, and accumulation areas, providing further insights into solute distribution and transport within the system (Bassingthwaighte et al., 2012).

A knowledge-driven qualitative Biological Regulatory Network (BRN) of HIF-1 was extracted from the literature. The selection of specific entities (HIF-1, ERK, VEGF, p53, β-catenin, AKT, GLUT-1, C-MYC, OGT) for the creation of the BRN is based on their significant contribution to complex cellular processes in cancer. Understanding these entities and their interactions is crucial in unraveling cellular control and investigating new therapeutics linked to cancer. These entities are intertwined within a complex network, where the activation or dysregulation of one entity sets off a chain reaction, influencing others and contributing to cancer progression. Based on the comprehensive signaling pathways shown in Figure 2, HIF-1, a transcription factor sensitive to reduced oxygen levels (hypoxia), initiates the activation of specific genes, including VEGF and GLUT-1. These genes are known to have a significant influence in facilitating angiogenesis and enhancing glucose uptake, respectively. The impact of the activation of VEGF and GLUT-1 is highly critical inside the hypoxic tumor microenvironment, specifically for tumor growth and metastasis. (Maxwell et al., 1997), (Wincewicz et al., 2007). As a result, the activation of ERK, a central regulator in cell signaling, leads to increased cell proliferation and survival, fueling uncontrolled cancer growth (Minet et al., 2000). The p53 protein, a critical factor in suppressing tumor growth, assumes a central position in regulating the cell cycle and programmed cell death, known as apoptosis, to maintain cellular homeostasis. Disruptions in the p53 gene’s functionality impair crucial regulatory processes, hence facilitating uncontrolled cellular proliferation, frequently observed in many human malignancies. It highlights the significant consequence of p53 in inhibiting abnormal cell growth and its involvement in preventing tumors (Sermeus and Michiels, 2011). Due to this, dysregulation of β-catenin within the Wnt signaling pathway disrupts normal cell adhesion and gene expression, thus raising cancer development and AKT’s role in cell survival and proliferation grants cancer cells a survival advantage (Cui et al., 2010). Moreover, the upregulation of GLUT-1 is strongly associated with the Warburg effect, a metabolic phenomenon observed in cancer cells characterized by enhanced glucose uptake (Li et al., 2015). Subsequently, C-MYC, an oncogene, boosts uncontrolled cell division, and OGT’s capacity to modify protein function can significantly impact cellular processes and potentially contribute to cancers (et Nurbubu, 2020). These entities constitute a highly complex and intertwined network, highlighting the significance of comprehending their roles within regulatory networks to unravel disease mechanisms and identify potential therapeutic targets. Qualitative modelling is employed to dissect these entities’ stepwise processes and interactions, providing a detailed understanding of how they influence each other and cellular behavior in cancer.

The finally selected network included fourteen interactions and nine biological entities, as shown in Figure 3. The selected activator entities, including HIF-1, VEGF, and ERK, create a positive feedback loop, which is recognized to yield numerous stable/deadlock states. A positive feedback loop comprises positive interactions and an even number of inhibitory or negative interactions (PLAHTE et al., 2011). It functions similarly to a toggle switch, simultaneously expressing just one of the two entities (Gardner et al., 2000). A negative circuit comprises a negative interaction of an odd number that results in homeostasis or periodic behavior, such as the interaction between C-MYC, VEGF, AKT, and β-catenin. Three complex HIF-1-based regulatory circuits generate cell proliferation and regulate oscillations. The circuits under consideration consist of three distinct positive feedback loops. The first loop involves the interaction between VEGF and ERK. The second loop incorporates VEGF, AKT, and p53. The third loop comprises C-MYC, VEGF, ERK, GLUT 1, and OGT. A comprehensive examination of these regulatory patterns provides useful insights into the various behaviors that the system could show. Moreover, the computation of logical parameters exposes the huge functional dynamics that have both positive/negative routes in a complicated system.

Computing logical parameters in biological regulatory networks is crucial for modelling complex systems, predicting network behavior under different conditions, and gaining insights into biological processes. The model trajectories are derived by examining logical parameters' binary values (0 or 1), visually represented as a state transition graph in Figure 5. These parameters are computed by utilizing Computational Temporal Logic (CTL) algorithms, which are driven by well-established qualitative observations (Baltazar et al., 2011).

The CTL data presented in Table 1 shows changes in the HIF-1 route, which is the first formula in the biological system that expresses high expression of VEGF, OGT, and GLUT-1, all of which are required for tumor cell proliferation, vasculogenesis, and metastasis (Chae et al., 2011), (Hendriksen et al., 2009), (Lei et al., 2020). Under hypoxia, hepatocellular carcinoma cells with high HIF-1 and GLUT-1 expression regulate tissue oxygen supply and energy metabolism (Chae et al., 2011), (Hendriksen et al., 2009), (Amann et al., 2009). The downregulation of Akt in hypoxic conditions is a part of the cellular response to adapt to the stress of low oxygen. This downregulation is thought to be a protective mechanism, as it helps to conserve energy and limit processes that require oxygen, such as cell proliferation. Additionally, the downregulation of AKT in hypoxia contributes to the activation of alternative survival pathways that are better suited for low-oxygen environments (Mottet et al., 2003). However, decreased AKT expression owing to dephosphorylating progressively leads (symbolized by “CTL operator ⇒“) to a stable pathogenic/oncogenic state (symbolized by CTL operator EF and AG) for all entities with high expression levels also for one path future state and all paths globally except AKT.

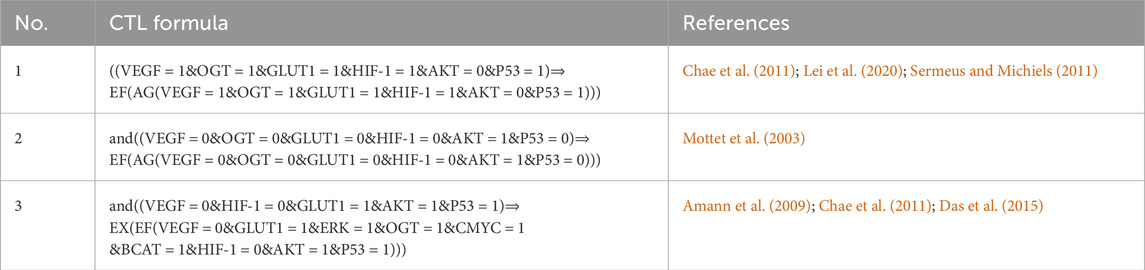
Table 1. The SMBioNet setup utilizes Computational Temporal Logic (CTL) equations to infer logical parameters. The second formula is specifically constructed to monitor homeostasis, whereas the other two are intended to observe a state of stability or homeostasis.

Only those parameters that fulfill the CTL formulae were chosen using the SMBioNet software (Helikar et al., 2011). It lists all the models in detail and picks the ones whose sets of parameters match the experimental data given as temporal logic formulae. As a result, eight sets of logical parameters were generated by SMBioNet, all of which point to a single deadlock state (1,1,1,1,1,0,1,1,1). The source code of SMBioNet and the output results used to calculate model parameters are found in (Supplementary Material S2). The existence or absence of resources determines every entity’s ability to adjust or modify its expression level. The present state of a gene is compared to values of logical parameters indicated in Supplementary Table S1 at each given time instant to determine its change in expression level. According to the calculated values, ERK maintains or increases its expression level in the presence of a HIF-1 activation signal.

In response to ERK activation, a simultaneous upregulation of HIF-1 expression is observed while the inhibitory influence of p53 remains present. Only in the absence of an AKT inhibitor signal does the tumor suppressor protein p53’s expression level rise. The third formula in Table 1 considered as VEGF and HIF-1 expression suppressed while maintaining GLUT-1, p53, and AKT expression levels. The interplay among glucose transporters (GLUTs), hypoxia-inducible factor 1 (HIF-1), and glycolytic enzymes has been observed across a spectrum of cancers (Chae et al., 2011; Amann et al., 2009; Das et al., 2015). However, particularly intriguing is the exploration of outcomes arising from the simultaneous inhibition of HIF-1 and activation of GLUT-1.

HIF-1 and GLUT-1 regulate mRNA and protein levels in human gastric and ovarian cancers (Amann et al., 2009). State transition graphs are primarily used to examine the mutual behavior of genes functioning in a biological system (Schwab et al., 2020). Figure 4 shows a heatmap of the eight sets of logical parameters SMBioNet created in this scenario. Model validation of these data sets confirms the chosen logical parameters, which offer insights into potential biological pathways associated with cancer invasion and recovery. Briefly, the induction of HIF-1 in the presence of ERK is a constant observation across all eight parameter sets, indicating that a parameter set that permits HIF-1 to reach its maximum threshold value of '1′may be harmful to cancer cells. In maintaining natural dynamic processes, these parameters (M8) allow for interactions across all nodes while maintaining their interdependencies for activation and suppression. The state transition graph represents these dynamics. The source code of the input models can be found in the (Supplementary Material S3). The computed values also show that when GLUT-1, VEGF, OGT, and the oncogene C-MYC upregulate, HIF-1 continues to be expressed at a higher level. On the other hand, activating the p53 inhibitor stops HIF-1 from rising above the typical threshold value. Furthermore, in the absence of AKT inhibitory signals, p53 expression rises, and GLUT-1 is activated in response to the HIF-1 signal (Yeung et al., 2008). Interpreting the trajectories within the state transition graph is essential to thoroughly understanding gene behavior in the context of a dynamic biological system.

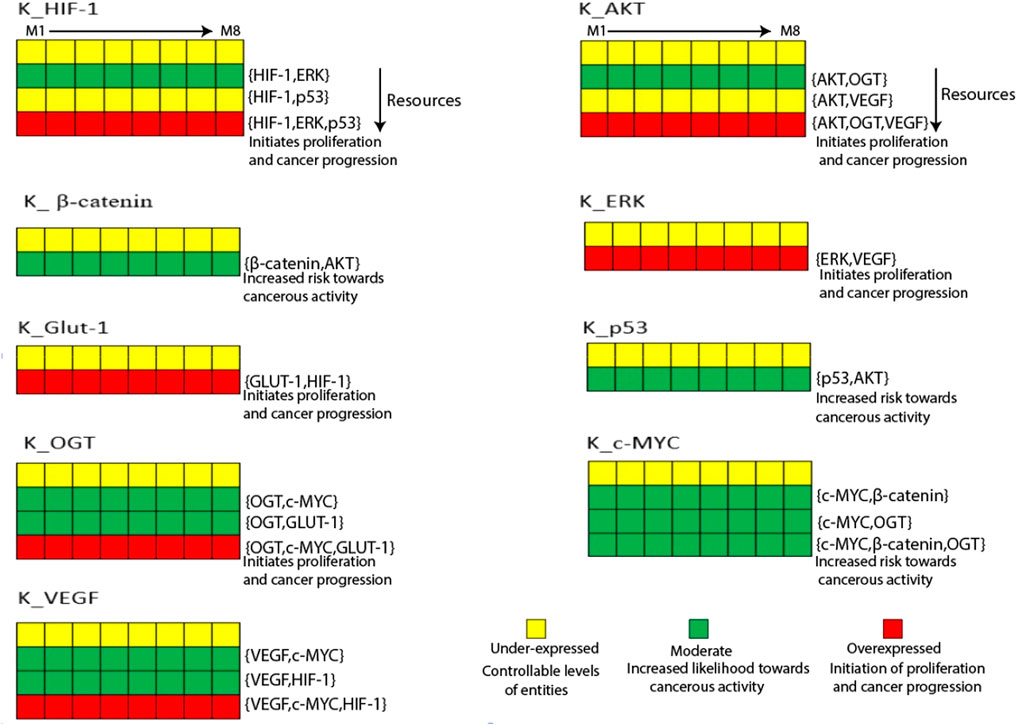
Figure 4. The Heatmap generated from the logical parameters computed on SMBioNet reveals the presence of eight distinct parameter sets. Among these, a preferred set of parameters was determined via model checking, and the results are visually depicted in the form of a heatmap, accompanied by their respective resources labeled as M1 through M8. Each column in this heatmap represents a distinct set of logical parameters, with green denoting moderate expression, red denoting overexpression, and yellow denoting under expression of an entity.

The Cytoscape software is employed to visualize the state transition graph consisting of 512 nodes (Figure 5). The state graph is created by the GINsim tool using the estimated SMBioNet parameters as indicated in the last column of Supplementary Table S1. The states of biological entities are arranged in a manner that reflects their betweenness centrality. The state graph represents the system’s status at any given time using an indicator containing the expression levels of all entities provided. These entities are ordered: (HIF-1, ERK, VEGF, p53, β-catenin, AKT, GLUT-1, C-MYC, OGT). A typical qualitative condition within the state graph in Figure 5 is distinguished by reduced expression levels of HIF-1, VEGF, ERK, GLUT-1, and OGT as well as the tumor suppressor genes C-MYC, p53. On the other hand, the pathogenic qualitative condition is characterized by increased levels of HIF-1, VEGF, GLUT-1, and ERK expression. This visual depiction facilitates comprehension of the dynamic functioning of the system and offers valuable insights into the shift from a healthy to a diseased state.

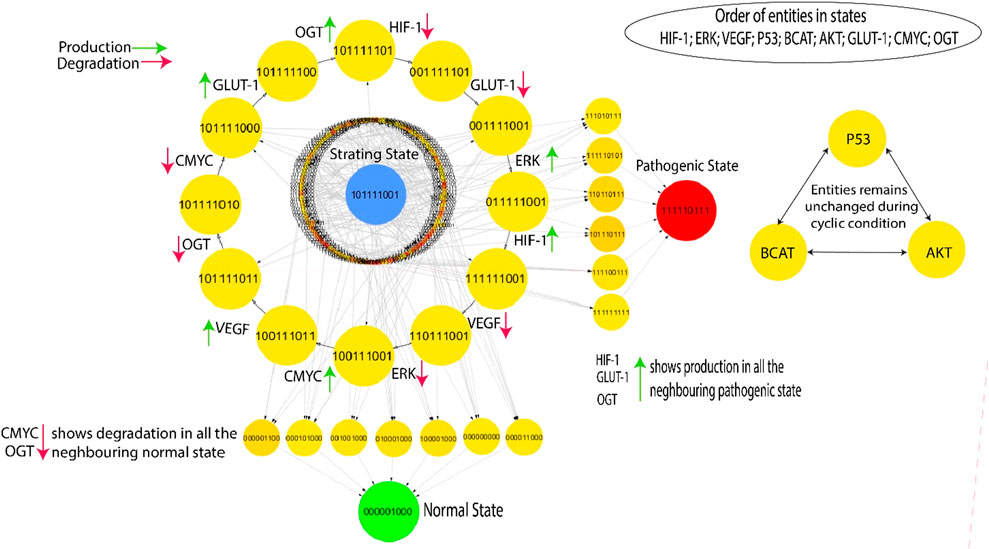
Figure 5. The highest betweenness and centrality cycle is retrieved at the outermost layer. The top layer entities show arrows (red and green) representing a specific entity’s production and degradation. Furthermore, the neighboring entities of the pathogenic state (111,110,111) show continuous activation of HIF, GLUT-1, and OGT, whereas the neighboring entities of the normal state (000,001,000) show continual degradation of C-MYC and OGT.

This qualitative state (0,0,0,0,0,0,0,0,0) in biological systems exhibits oscillatory behaviors or homeostasis under normal conditions; in a normal state, the overall behavior of the system shows cyclic. As a result, a good qualitative model should include disease/pathogenic and typical homeostatic characteristics such as cycles and closed paths. Under typical physiological conditions, the biological system exhibits homeostasis, defined by the downregulation of oncogenes such as OGT, GLUT-1, and C-MYC. This state is achieved when VEGF activation is absent and reduced levels of ERK. In contrast, a pathological condition characterized by high levels of HIF-1 and oncogene expression is indicated by the trajectory (1,1,1,1,1,0,1,1,1) as illustrated in Figure 5. The transition from homeostasis to a pathogenic state is a significant alteration in the system’s behavior, frequently linked to the progression of the disease. The deadlock state’s mediate predecessors up to two layers have low betweenness centrality, illustrated by circles with significantly greater influence and yellow color. This indicates a greater chance of the infected system regaining stability by passing through a sequence of stable states that hold less importance within the recovery process, as denoted by their low betweenness centrality. However, high betweenness centrality indicates essential nodes that control information flow and influence network dynamics, offering insights into key regulators or potential intervention points in disease mechanisms. The previously mentioned trajectories are crucial in enabling interactions inside the system, significantly enhancing its adaptability and flexibility. The model (Figure 5) highlights a series of cycles computed using the GINsim software, which is shown as the outermost circle. The states within the cycles demonstrate significant levels of betweenness centrality, as denoted by the yellow circles, whereas red circles depict the states with low betweenness centrality. This representation helps us better understand the network structure and how it affects the system’s dynamics.

The occurrence of cycles within the model holds significant importance, enabling the finding of the most probable biological cycle. Figure 5 presents a computed cycle utilizing the Cytoscape tool, which uses betweenness centrality to rank states. The ranking of states based on their betweenness centrality is further information in (Supplementary Material S4). In this visual depiction, nodes with larger diameters indicate states with greater betweenness centrality. This methodology facilitates the identification of crucial states within the network, providing insights into the most significant components and their possible effects on biological processes. The cycle with the highest betweenness centrality: (1,0,1,1,1,1,1,0,1) → (0,0,1,1,1,1,1,0,1) → (0,0,1,1,1,1,0,0,1) → (0,1,1,1,1,1,0,0,1) → (1,1,1,1,1,1,0,0,1) → (1,1,0,1,1,1,0,0,1) → (1,0,0,1,1,1,0,0,1) → (1,0,0,1,1,1,0,1,1) → (1,0,1,1,1,1,0,1,1) → (1,0,1,1,1,1,0,1,0) → (1,0,1,1,1,1,0,0,0) → (1,0,1,1,1,1,1,0,0) shows oscillations of all entities except p53, β-catenin and AKT. The cycle indicates that homeostasis requires continual activation of p53, β-catenin and AKT. By disrupting this process, commonly achieved by the overexpression of HIF-1, GLUT-1, and OGT, a transition can occur, leading to either a malignant state (1,1,1,1,1,0,1,1,1) or a state of recovery (0,0,0,0,0,1,0,0,0). This binary sequence appears to represent a state where several signaling pathways and molecules associated with cancer are activated or upregulated. This could indicate a malignant state with increased cell proliferation, survival, and angiogenesis. The “0”for AKT might suggest a potential inhibition or downregulation of this pathway, which is often associated with anti-apoptotic signals. The transition process is made possible through the downregulation of C-MYC and OGT, two crucial factors involved in cellular growth and metabolism (Ferrer et al., 2014), (Jóźwiak et al., 2014). The previously mentioned dynamics highlight the system’s susceptibility to changes in crucial regulatory elements, which affect the balance between normal and disease states.

The cyclic trajectories illustrated in Figure 5 precisely indicate the presence of p53, β-catenin, and AKT proteins. These entities fulfill a useful regulatory function in the hypoxia-inducible factor (HIF) system, aiding in preserving homeostasis within the model. On the other hand, when HIF-1 expression is dysregulated and causes the activation of cellular proliferation mechanisms, particularly ERK and GLUT-1, it has the potential to give rise to problems such as diabetes or more severe illnesses such as oncogenes is. This highlights the crucial significance of these regulatory components in regulating the dynamic equilibrium of the system and its potential deviation toward pathological conditions.

The subgraphs are extracted from the state graph and shown in Figures 6, 7. These subgraphs depict the behavior of states step by step to induce changes and show how the biochemical system goes toward cancer progression or recovery state. In light of the complex structure of the broad state network that arises from qualitative modelling, we utilized the concept of average betweenness centrality, as outlined in Definition 6, to identify significant trajectories. This methodology enabled us to prioritize significant trajectories without needing to examine each individually, as shown in Figure 6. The chosen trajectory was decided by identifying the maximum betweenness centrality. This trajectory initiated from the initial state (1,0,1,1,1,0,0,1) and led to either the pathogenic or deadlock state (1,1,1,1,1,0,1,1,1). Proto-oncogenes such as C-MYC and AKT are essential constituents of the signaling network under normal physiological circumstances, exerting significant influence on the regulation of cellular development (Hers and Vincent, 2023), (Asano et al., 2004). The previous path selection highlights the importance of these parameters and their possible influence on the shift from a normal to a pathogenic state.