For the mHRJSD approach, the proposed directionality index was further extended to determine the dominant coupling direction and assess the driver-response relationships in multivariate (n = 3) systems.
For a multivariate system (x,y,z), the single-word family occurrences p(wf) from the x-, y- and z-plane (pfX, pfY, pfZ) from the 8 × 8 × 8 pattern family density matrix Wf were used to calculate DmHRJSD (Equations 14–16). Thereby, for each coupling pathway, one directionality index was calculated (e.g., two interacting time series: x and y with z as the covariate |). Thus, for the coupling between the time series x and y with covariate z, the directionality index (Equation 14) is defined as:
DmHRJSDx,y|z=−∑i=1npfx|zi−pfy|zipfx|zi+pfy|zi/n (14)For the coupling between the time series x and z with covariate y, the directionality index (Equation 15) is defined as:
DmHRJSDx,z|y=−∑i=1npfx|yi−pfz|yipfx|yi+pfz|yi/n (15)For the coupling between the time series y and z with covariate x, the directionality index (Equation 16) is defined as:
DmHRJSDy,z|x=−∑i=1npfy|xi−pfz|xipfy|xi+pfz|xi/n (16)If DmHRJSD(x,y|z) is positive, driving (→) from system 1 (x) to system 2 (y) predominates (Equation 17) and becomes negative for the opposite case (Equation 18).
DmHRJSDx,y|z>0;x|z→y|z (17) DmHRJSDx,y|z<0;y|z→x|z (18)If DmHRJSD(x,z|y) is positive, driving (→) from system 1 (x) to system 2 (z) predominates (Equation 19) and becomes negative for the opposite case (Equation 20).
DmHRJSDx,z|y>0;x|y→z|y (19) DmHRJSDx,z|y<0;z|y→x|y (20)If DmHRJSD(y,z|x) is positive, driving (→) from system 1 (y) to system 2 (z) predominates (Equation 21) and becomes negative for the opposite case (Equation 22).
DmHRJSDy,z|x>0;y|x→z|x (21) DmHRJSDy,z|x<0;z|x→y|x (22)Thus, three indices were derived, which are subsequently used to determine the strongest driver and the most dominant responder in the overall system. Therefore, all three indices were compared to whether they were greater (+) or less than 0 (−) (Table 1). This means that if the index is greater than zero for the multivariate interaction, “+” is set; if the index is less than zero, “−” is set. Afterward, the sum of the three comparisons of the three directionality indices was determined and counted. If a time series is present twice (++ or −− or +− or −+) as a driver, it dominates the overall system and is determined as the primary driver **DmHRJSD, and if a time series is present only once (+ or −), then it is determined as the secondary driver *DmHRJSD of the overall system, and the non-occurring time series is the dominant responder −DmHRJSD.
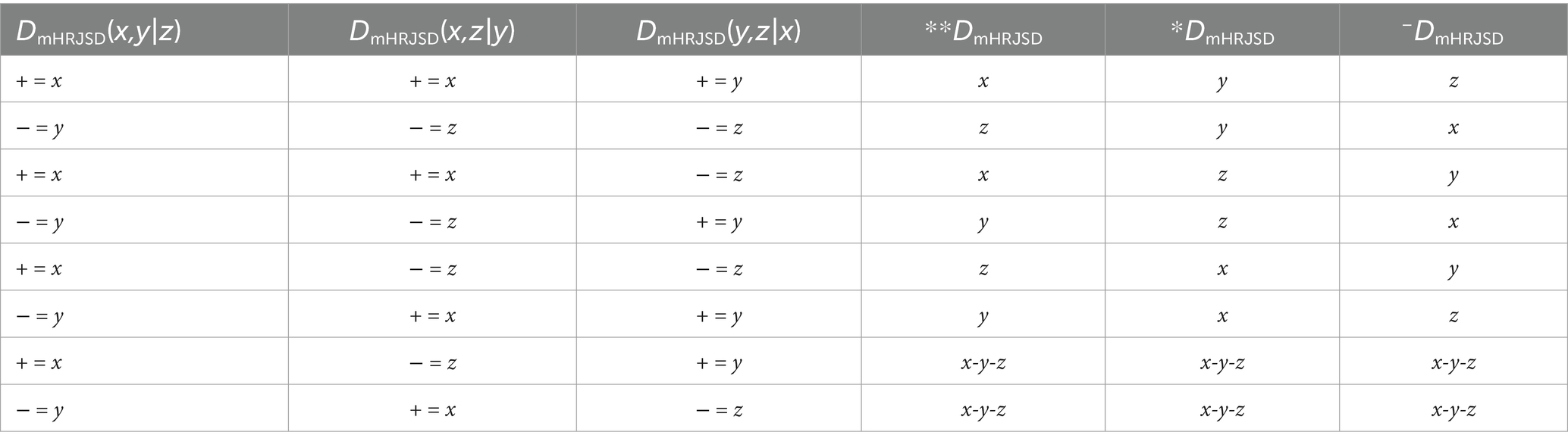
Table 1. Determination of the primary driver (**DmHRJSD), secondary driver (*DmHRJSD), and the dominant responder (−DmHRJSD) in a multivariate system derived from the directionality indices DmHRJSD(x,y|z), DmHRJSD(x,z|y), and DmHRJSD(y,z|x).
For exapmple: DmHRJSD(x,y|z) > 0, DmHRJSD(x,z|y) > 0, and DmHRJSD(y,z|x) > 0, resulting in (+++ equal to x-x-y) or DmHRJSD(x,y|z) < 0, DmHRJSD(x,z|y) > 0, and DmHRJSD(y,z|x) < 0, resulting in (−+− equal to y-x-z). The indices **DmHRJSD, *DmHRJSD, and −DmHRJSD are determined by their absolute values in descending order of importance of their values. For the first example (+++), we have information flows from x → y, x → z, and y → z resulting in x as **DmHRJSD, y as *DmHRJSD, and z as −DmHRJSD. For the second example (−+−), we have information flows from y → x, x → z, and z → y, resulting in a closed-loop where **DmHRJSD, *DmHRJSD, and −DmHRJSD cannot be clearly determined (these options are represented by the last two lines in the Table 1).
The simulated linear and non-linear AR systems were validated with two additional approaches: the normalized short-time partial directed coherence (NSTPDC) (Adochiei et al., 2013) and the multivariate transfer entropy (MuTE) (Montalto et al., 2014). Both methods allow us to determine the coupling direction. NSTPDC mainly detects linear coupling, whereas MuTE mainly detects non-linear coupling. In short, NSTPDC is based on an m-dimensional AR model with the order p and allows determining linear Granger causality in the frequency domain. Mute is an information-theoretical approach that detects the information transfer between multivariate joint processes and discovers purely non-linear interactions with a range of interaction delays. We applied in-house software in the programming environment MatlabR2013b.
3 Results 3.1 Results of simulated systems to validate DHRJSDAll three methods, HRJSD, NSTPDC, and MuTE, calculated a directionality index D (DHRJSD, DNSTPDC, DMuTE), which was used for validation. These three indices have in common that if the index is positive, driving (→) from system 1 (x) to system 2 (y) predominates and becomes negative for the opposite case that system 2 (y) is driving system 1 (x) (Table 2). Table 2 presents the results of the simulated linear and non-linear AR models with the underlying simulated driver-response relationships in a multivariate context and the results of the applied directionality indices.
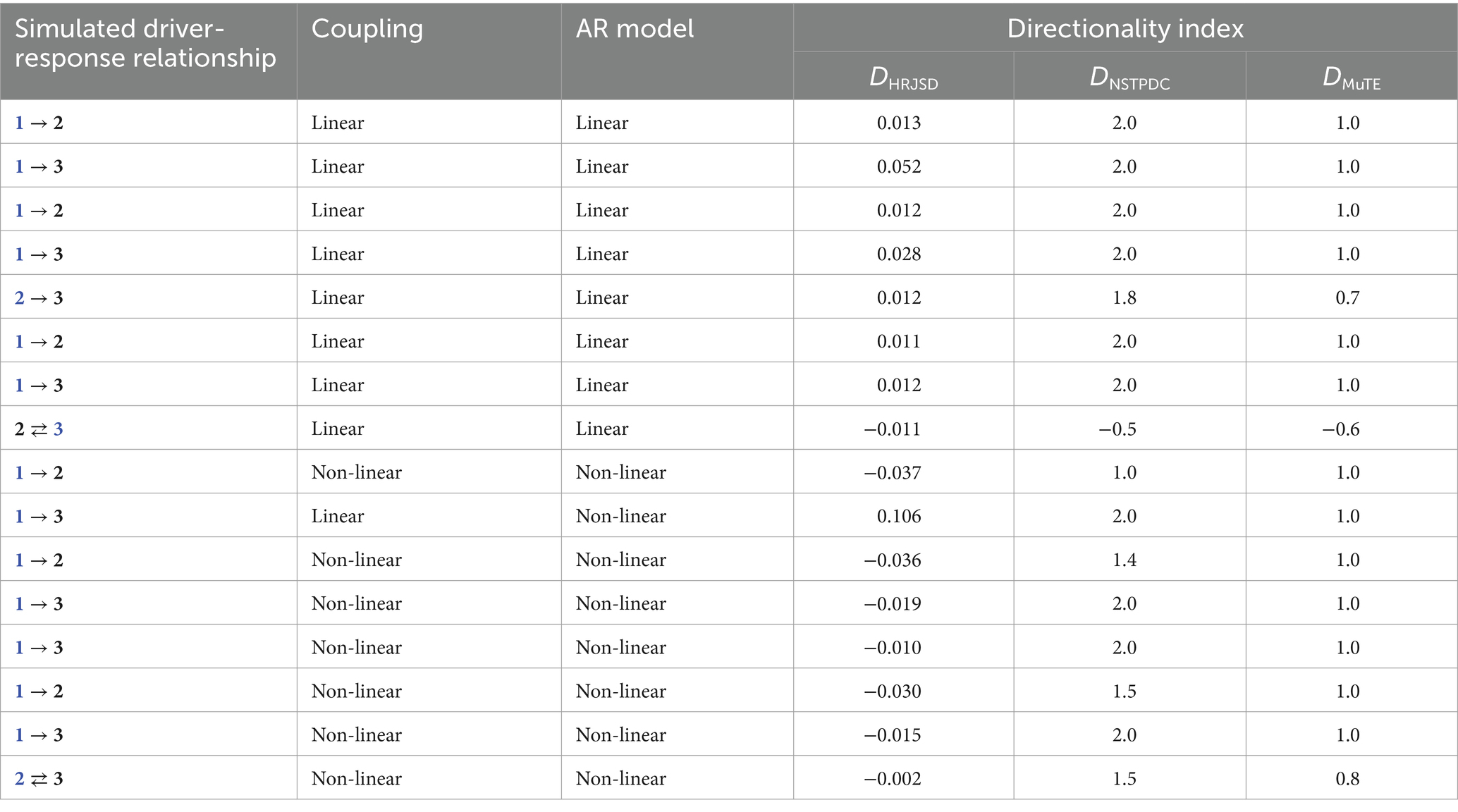
Table 2. Results of simulated linear and non-linear autoregressive (AR) systems to validate the directionality index DHRJSD (blue: driver variable).
For example, here, the first two rows are explained where the information flows were simulated with a linear AR model, linearly coupled variables, and simulated driver-response relationships 1 → 2 and 1 → 3 (blue represents the simulated driver variable). That means time series 1 transfers information to time series 2 and 3. The coupling directions are from 1 to 2 and 1 to 3.
Linear system 1:
1 → 2 and 1 → 3: DHRJSD, DNSTPDC, and DMuTE are positive; correct classification of the predominating coupling directions (1 is the driver).
Linear system 2:
1 → 2, 1 → 3, 2 → 3: DHRJSD, DNSTPDC, and DMuTE are positive; correct classification of the predominating coupling directions (1 and 2 are drivers).
Linear system 3:
1 → 2, 1 → 3: DHRJSD, DNSTPDC, and DMuTE are positive; correct classification of the predominating coupling directions (1 is the driver).
2⇄3: DHRJSD, DNSTPDC, and DMuTE are negative; correct classification of the predominating coupling direction (3 is the driver).
For the linear AR model with purely linear couplings among the three variables (1, 2, 3), all directionality indices (DHRJSD, DNSTPDC, DMuTE) were able to correctly detect the predominating coupling directions and the related driver variable.
Non-linear system 1 (Table 2):
1 → 2: DNSTPDC and DMuTE are positive; correct classification of the predominating coupling direction (1 is the driver).
DHRJSD is negative; incorrect classification of the predominating coupling direction. DHRJSD detects variable 2 as the driver.
1 → 3: DHRJSD, DNSTPDC, and DMuTE are positive; correct classification of the predominating coupling direction (1 is the driver).
Non-linear system 2:
1 → 2, 1 → 3, 2 → 3: DNSTPDC and DMuTE are positive; correct classification of the predominating coupling directions (1 and 2 are drivers).
DHRJSD is negative; incorrect classification of the predominating coupling directions. DHRJSD detects variables 2 and 3 as the drivers.
Non-linear system 3:
1 → 2, 1 → 3, 2 ⇄3: DNSTPDC and DMuTE are negative; correct classification of the predominating coupling directions (1 and 2 are drivers).
DHRJSD is negative; incorrect classification of the predominating coupling directions. DHRJSD detects variables 2 and 3 as the drivers.
For the non-linear AR model with purely non-linear couplings among the three variables (1, 2, 3), only NSTPDC and MuTE were able to correctly detect the predominating coupling directions and the related driver variable. DHRJSD could partly detect the dominating coupling direction in non-linear systems (non-linear system 1).
The proposed directionality index DHRJSD derived from the HRJSD approach is able to correctly detect the dominating coupling direction in linear bivariate coupled systems but is only partly able to detect the dominating coupling direction in non-linear bivariate coupled systems. Due to this limitation, in detailed investigations to determine the coupling direction, other methods should be used in addition to DHRJSD (e.g., MuTE), which can also correctly determine the dominant driver-response relationships in pure non-linear systems.
3.2 Results of simulated systems to validate DmHRJSDSimilarly to validating DHRJSD for the bivariate system, simulated data was used to validate DmHRJSD. Therefore, a multivariate linear Gaussian AR model was applied to generate a set of multivariate linear time series (n = 100) with a normal distribution of the variables (Baccala and Sameshima, 2001; Montalto et al., 2014). For the linear model, two different multivariate coupled systems were generated (Equations 8, 9) with different mutual influences (unidirectional, bidirectional) between the time series (Figures 3B,C). Non-linear AR models were not applied since DHRJSD seems to only partly detect the correct driver-responder relationship between non-linear coupled time series.
The results of the two multivariate coupled linear AR systems showed that the determination of the multivariate directionality index DmHRJSD works properly, as well as the determination of the primary driver **DmHRJSD, the secondary driver *DmHRJSD, and dominant responder −DmHRJSD in the multivariate systems (Table 3).

Table 3. Determination of the primary driver (**DmHRJSD), secondary driver (*DmHRJSD), and the dominant responder (−DmHRJSD) derived from the directionality indices DmHRJSD(x,y|z), DmHRJSD(x,z|y), and DmHRJSD(y,z|x) for two simulated multivariate coupled systems (LS2, LS3).
Linear system 2, LS2:
x1 → x2: DmHRJSD(x1,x2|x3) is positive; correct classification of the dominating coupling direction (x1 is driver).
x1 → x3: DmHRJSD(x1,x3|x2) is positive; correct classification of the dominating coupling direction (x1 is driver).
x2 → x3: DmHRJSD(x2,x3|x1) is positive; correct classification of the dominating coupling direction (x2 is driver).
From this results that:
DmHRJSD(x1,x2|x3) = x1 and DmHRJSD(x1,x3|x2) = x1 ⇒ **DmHRJSD = x1.
DmHRJSD(x2,x3|x1) = x2 ⇒ *DmHRJSD = x2.
⇒ −DmHRJSD = x3.
For the coupled multivariate linear AR model (LS2), the correct driver-responder relationships were classified with x1 as the primary driver, x2 as the secondary driver, and x3 as the responder of the system, as it was simulated.
Linear system 3, LS3:
x1 → x2: DmHRJSD(x1,x2|x3) is positive; correct classification of the dominating coupling direction (x1 is driver).
x1 → x3: DmHRJSD(x1,x3|x2) is positive; correct classification of the dominating coupling direction (x1 is driver).
x2⇄x3: DmHRJSD(x2,x3|x1) is negative; correct classification of the dominating coupling direction (x3 is driver).
From this results that:
DmHRJSD(x1,x2|x3) = x1 and DmHRJSD(x1,x3|x2) = x1 ⇒ **DmHRJSD = x1.
DmHRJSD(x2,x3|x1) = x3 ⇒ *DmHRJSD = x3.
⇒ −DmHRJSD = x2.
For the coupled multivariate linear AR model (LS3), the correct driver-responder relationships were classified with x1 as the primary driver, x3 as the secondary driver, and x2 as the responder of the system, as it was simulated.
The mHRJSD approach contains multivariate directionality indices DmHRJSD (DmHRJSD(x,y|z), DmHRJSD(x,z|y), and DmHRJSD(y,z|x)), allowing us to determine the primary driver **DmHRJSD, the secondary driver *DmHRJSD, and the dominant responder −DmHRJSD in multivariate systems. Therefore, it has to be assumed that the time series to be analyzed are at least weakly coupled with each other. Limiting factors are that the proposed directionality index DmHRJSD derived from the mHRJSD approach can only correctly detect the driver-responder relationships in linear coupled systems and cannot detect the driver-responder relationships in non-linear coupled systems. The mHRJSD approach can evaluate direct causal information transfer in multivariate systems. Despite this limitation of DmHRJSD, the feature to assess the driver-response relationships in multivariate systems is not implemented in any of the existing symbolization approaches and thus clearly complements the existing coupling approaches.
4 DiscussionThe HRJSD approach emphasizes a clear characterization of how the couplings are composed by regulatory aspects of the ANS; it is able to quantify the coupling direction (directionality index: DHRJSD) in linear and non-linear coupled systems, which was not possible with existing symbolization approaches, neither for bivariate nor for multivariate systems, and assesses the driver-response relationships in bivariate (n = 2) and multivariate (n = 3) systems.
The newly developed directionality indices derived from (m)HRJSD are based on simple mathematical symbolization principles and simple calculation procedures, enabling a comprehensive understanding of the underlying couplings in a fast and easy way, and do not have the limitations of existing approaches. The main advantages of the (m) HRJSD-derived directionality indices are that they are insensitive to non-stationary time series; they are able to capture couplings through a simple, fast, and easy-to-implement symbolization procedure; they are scale-invariant; they are independent of time series length, model order selection, and significance level determination procedure. Moreover, clear advantages of using DHRJSD over, e.g., MuTE are that with DHRJSD, a multivariate interaction can be classified in the overall system in such a way that it can be determined which variable in the system generates the primary and secondary information flow and which variable only acts as a responder in the system. This assessment is currently only possible for linear systems. Further research with other models and time delays will provide further insight into DHRJSD. Most of the already established coupling approaches, e.g., partial directed coherence (PDC) or directed transfer function, depend on the reliability of the fitted multivariate autoregressive model (MAR) (i.e., optimal model order, epoch length) and a significance level has to be used for both to avoid spurious interactions (Schulz et al., 2013a). In general, most of these coupling approaches have high degrees of freedom, are not standardized in their preconditions (e.g., preprocessing steps, parameter settings, time-series length, model order selection, significance level determination, scale-independent data, and stationarity), and have been validated using physiological and pathophysiological cases (Schulz et al., 2013a).
The HRJSD approach includes different threshold levels and a directionality index, DHRJSD. The validation studies showed that the directionality index DHRJSD is able to correctly detect the dominating coupling direction in linear coupled systems but is partly able to detect the dominating coupling direction in non-linear coupled systems. It is an intriguing observation that, within non-linear systems, where linear couplings may also prevail, the method can precisely detect these linear couplings. This suggests that the method can be employed to identify the part of the underlying coupling in a system, irrespective of its linear or non-linear nature and regardless of the type (linear or non-linear) of coupling between the variables (Table 2, NLS1, 1→3).
The HRJSD approach and other symbolization approaches are only able to analyze bivariate couplings, whereas the HRJSD approach is also able to determine the driver-responder relationship; facing this, the mHRJSD approach is able to quantify multivariate couplings and to determine dominant driver-responder relationship in multivariate coupled systems. These are outstanding new features for coupling analyses based on symbolizations. The mHRJSD approach facilitates multivariate analysis by incorporating a third time series, enabling the coarse-grained evaluation of time series dynamics. As outstanding and unique features of the mHRJSD approach are the implemented multivariate directionality indices DmHRJSD (DmHRJSD(x,y|z), DmHRJSD(x,z|y), and DmHRJSD(y,z|x)) allowing us to determine the primary driver **DmHRJSD, the secondary driver *DmHRJSD, and the dominant responder −DmHRJSD in multivariate systems (assumption: weakly coupled system). The simulation procedure revealed that the proposed directionality index DmHRJSD derived from the mHRJSD approach is able to correctly detect the driver-responder relationships in linear coupled systems. Moreover, the mHRJSD approach is able to evaluate the direct causal information transfer in multivariate systems.
However, given the limitation of DHRJSD (e.g., MuTE) in fully determining coupling direction in nonlinear coupled systems, additional methods should be employed. The method-specific characteristics of the different coupling approaches operate in different domains in the assessment of coupling (strength and direction) and causality, and there is currently no superior approach that can combine all the advantages in a single approach. While non-linear methods study complex signal interactions, linear methods favor the frequency domain representation of biological signals (characterizing the connectivity between specific oscillatory components) (Schulz et al., 2013a).
Due to this restriction so far, it would be of great interest to test other models and see how the newly proposed directional indices are able to evaluate driver-response relationships. Here, the physiome as a computerized quantitative model could be an option. The physiome is the definitive quantitative and integrated description of the functional behavior of the physiological state of an individual or species. The physiome describes the physiological dynamics of the normal, intact organism. It is built upon information and structure, namely the genome, proteome, and morpheme. The physiome must define relationships from genome to organism and from functional behavior to gene regulation. Quantitative models in physiome are unlike any other database-driven research area, including bioinformatics, network biology, or big data analysis. The physiomic model is a repository of previous data and a tool for testing and predicting results by varying factors. Thereby, models can be defined at various levels of abstraction: the conceptual level, the mathematical level, the formulation level, and the solution level (Leem, 2016). Physiome and network physiology are very similar as they pursue integrative concepts. The multidisciplinary field of network physiology studies how different physiological systems and subsystems interact to regulate their functions. It looks at how these systems interact across different spatial and temporal scales, from cellular to organism levels. It also looks at how they communicate and work together to generate different physiological states and behaviors in health and disease (Bartsch et al., 2015b; Ivanov et al., 2016a; Ivanov, 2021).
The cardiovascular, cardiorespiratory, and central networks are intricate physiological systems with both direct and indirect interactions. In the investigation of these networks, bivariate approaches are frequently employed. Nevertheless, it seems reasonable to posit that multivariate approaches will become more prevalent in place of bivariate ones, given that they enhance the characterization of causal or non-causal interrelationships between the networks. For instance, multivariate coupling analysis, for example, heart rate, systolic blood pressure, respiration, and central activity, may provide more advanced information about the complex autonomic network in physiological and pathophysiological conditions than uni- and bivariate approaches.
For instance, interactions within the cardiorespiratory network are primarily reflected in respiratory sinus arrhythmia (RSA), characterized by rhythmic fluctuation in cardiac cycle intervals in relation to respiration. Two principal mechanisms have been proposed to explain the RSA. The first is the central influence of respiration on vagal cardiac motor neurons, and the second is the impact of respiration on intrathoracic pressure. In the context of central networks, the concepts of functional connectivity and neurophysiological brain processes are significant. These include bottom-up and top-down processing, whereby information flows from higher brain regions to peripheral end organ systems or vice versa (Schulz et al., 2013a; Schulz et al., 2018).
In further steps, the new directionality indices will be applied and tested based on already analyzed and existing clinical data (cardiovascular system, cardiorespiratory system, central autonomic network) (Schulz et al., 2016; Schulz et al., 2018; Schulz et al., 2019) and compared with other methods in terms of their classification rate and accuracy. Moreover, further testing is necessary to ensure the robustness of the new directionality indexes and how time delays in the simulated models, as well as within the calculation procedure, influence the directionality results and the driver-response relationships.
Data availability statementThe original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributionsSS: Conceptualization, Formal analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing. AS: Writing – review & editing. K-JB: Writing – review & editing. JH: Writing – review & editing. GS: Writing – review & editing. AV: Writing – review & editing, Methodology, Supervision, Validation.
FundingThe author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by funding from the Software AG Stiftung (SE-P 14572).
AcknowledgmentsI would also like to thank my former colleague and friend, Dipl.-Ing. Rico Schröder, who helped me with his expertise in solving problems that arose during the study. The successful, long-term collaboration with him has strongly influenced the content of this study.
Conflict of interestThe authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.
Generative AI statementThe author(s) declare that no Gen AI was used in the creation of this manuscript.
Publisher’s noteAll claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
ReferencesAdochiei, F., Schulz, S., Edu, I., Costin, H., and Voss, A. (2013). A new normalised short time PDC for dynamic coupling analyses. Biomed Tech (Berl) 58:1. doi: 10.1515/bmt-2013-4167
PubMed Abstract | Crossref Full Text | Google Scholar
Aguirre, R. R., Mustafa, M. Z., Dumenigo, A., Schulz, S., Voss, A., Goubran, B., et al. (2018). Influence of acute antipsychotic treatment on cardiorespiratory coupling and heart rate variability. Cureus 10:e2066. doi: 10.7759/cureus.2066
PubMed Abstract | Crossref Full Text | Google Scholar
Arnhold, J., Grassberger, P., Lehnertz, K., and Elger, C. E. (1999). A robust method for detecting interdependences: application to intracranially recorded EEG. Physica D: Nonlinear Phenomena 134, 419–430. doi: 10.1016/S0167-2789(99)00140-2
Crossref Full Text | Google Scholar
Bashan, A., Bartsch, R. P., Kantelhardt, J. W., Havlin, S., and Ivanov, P. (2012). Network physiology reveals relations between network topology and physiological function. Nat. Commun. 3:702. doi: 10.1038/ncomms1705
PubMed Abstract | Crossref Full Text | Google Scholar
Baumert, M., Walther, T., Hopfe, J., Stepan, H., Faber, R., and Voss, A. (2002). Joint symbolic dynamic analysis of beat-to-beat interactions of heart rate and systolic blood pressure in normal pregnancy. Med. Biol. Eng. Comput. 40, 241–245. doi: 10.1007/BF02348131
PubMed Abstract | Crossref Full Text | Google Scholar
Beissner, F., Meissner, K., Bar, K. J., and Napadow, V. (2013). The autonomic brain: an activation likelihood estimation meta-analysis for central processing of autonomic function. J. Neurosci. 33, 10503–10511. doi: 10.1523/JNEUROSCI.1103-13.2013
PubMed Abstract | Crossref Full Text | Google Scholar
Candia-Rivera, D., Chavez, M., and De Vico Fallani, F. (2024). Measures of the coupling between fluctuating brain network organization and heartbeat dynamics. Netw Neurosci 8, 557–575. doi: 10.1162/netn_a_00369
PubMed Abstract | Crossref Full Text | Google Scholar
Chen, W. G., Schloesser, D., Arensdorf, A. M., Simmons, J. M., Cui, C., Valentino, R., et al. (2021). The emerging science of Interoception: sensing, integrating, interpreting, and regulating signals within the self. Trends Neurosci. 44, 3–16. doi: 10.1016/j.tins.2020.10.007
PubMed Abstract | Crossref Full Text | Google Scholar
Faes, L., Marinazzo, D., Jurysta, F., and Nollo, G. (2015). Linear and non-linear brain-heart and brain-brain interactions during sleep. Physiol. Meas. 36, 683–698. doi: 10.1088/0967-3334/36/4/683
PubMed Abstract | Crossref Full Text | Google Scholar
Ivanov, P. C., Liu, K. K., and Bartsch, R. P. (2016). Focus on the emerging new fields of network physiology and network medicine. New J. Phys. 18:100201. doi: 10.1088/1367-2630/18/10/100201
PubMed Abstract | Crossref Full Text | Google Scholar
Kurths, J., Voss, A., Saparin, P., Witt, A., Kleiner, H. J., and Wessel, N. (1995). Quantitative analysis of heart rate variability. Chaos 5, 88–94. doi: 10.1063/1.166090
PubMed Abstract | Crossref Full Text | Google Scholar
Lombardi, A., Guaragnella, C., Amoroso, N., Monaco, A., Fazio, L., Taurisano, P., et al. (2019). Modelling cognitive loads in schizophrenia by means of new functional dynamic indexes. NeuroImage 195, 150–164. doi: 10.1016/j.neuroimage.2019.03.055
PubMed Abstract | Crossref Full Text | Google Scholar
Marwan, N., Zou, Y., Wessel, N., Riedl, M., and Kurths, J. (2013). Estimating coupling directions in the cardiorespiratory system using recurrence properties. Philos. Trans. A Math. Phys. Eng. Sci. 371:20110624. doi: 10.1098/rsta.2011.0624
PubMed Abstract | Crossref Full Text | Google Scholar
McAllen, R. M. (1976). Proceedings: inhibition of the baroreceptor input to the medulla by stimulation of the hypothalamic defence area. J. Physiol. 257, 45P–46P
PubMed Abstract | Google Scholar
Montalto, A., Faes, L., and Marinazzo, D. (2014). MuTE: a MATLAB toolbox to compare established and novel estimators of the multivariate transfer entropy. PLoS One 9:e109462. doi: 10.1371/journal.pone.0109462
PubMed Abstract | Crossref Full Text | Google Scholar
Novak, V., Novak, P., De Champlain, J., Le Blanc, A. R., Martin, R., and Nadeau, R. (1993). Influence of respiration on heart rate and blood pressure fluctuations. J. Appl. Physiol. 74, 617–626. doi: 10.1152/jappl.1993.74.2.617
PubMed Abstract | Crossref Full Text | Google Scholar
Palus, M., Komarek, V., Hrncir, Z., and Sterbova, K. (2001). Synchronization as adjustment of information rates: detection from bivariate time series. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 63:046211. doi: 10.1103/PhysRevE.63.046211
PubMed Abstract | Crossref Full Text | Google Scholar
Palus, M., and Stefanovska, A. (2003). Direction of coupling from phases of interacting oscillators: an information-theoretic approach. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 67:055201. doi: 10.1103/PhysRevE.67.055201
PubMed Abstract | Crossref Full Text | Google Scholar
Quiroga, R. Q., Arnhold, J., and Grassberger, P. (2000). Learning driver-response relationships from synchronization patterns. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 61, 5142–5148. doi: 10.1103/PhysRevE.61.5142
PubMed Abstract | Crossref Full Text | Google Scholar
Rea, P. (2016). “Chapter 1 - overview of the nervous system” in Essential clinically applied anatomy of the peripheral nervous system in the head and neck. ed. P. Rea (London, United Kingdom: Academic Press), 1–20.
Schiff, S. J., So, P., Chang, T., Burke, R. E., and Sauer, T. (1996). Detecting dynamical interdependence and generalized synchrony through mutual prediction in a neural ensemble. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 54, 6708–6724. doi: 10.1103/PhysRevE.54.6708
PubMed Abstract | Crossref Full Text | Google Scholar
Schulz, S., Adochiei, F. C., Edu, I. R., Schroeder, R., Costin, H., Bar, K. J., et al. (2013a). Cardiovascular and cardiorespiratory coupling analyses: a review. Philos. Trans. A Math. Phys. Eng. Sci. 371:20120191. doi: 10.1098/rsta.2012.0191
Crossref Full Text | Google Scholar
Schulz, S., Bolz, M., Bär, K. J., and Voss, A. (2016). Central- and autonomic nervous system coupling in schizophrenia. Philos. Trans. A Math. Phys. Eng. Sci. 374:20150178. doi: 10.1098/rsta.2015.0178
PubMed Abstract | Crossref Full Text | Google Scholar
Schulz, S., Castro, M.R., Giraldo, B., Haueisen, J., and Voss, A. (2017a). "Multivariate high resolution joint symbolic dynamics (mHRJSD): a new tool to analyze couplings in physiological networks.", in: Biomedical engineering / Biomedizinische Technik).
留言 (0)