1 Introduction

Policy assessment constitutes a vital component of the national governance framework (1). A scientific and accurate assessment of policy impacts is essential for the modernization of the national governance system and its capacity (2). Traditional policy assessment predominantly utilizes data from sources like official statistical yearbooks, publicly accessible questionnaire databases, and field surveys. The main objective of policy assessment is to empirically validate economic theories (3). In contrast, public health policy evaluations often require integrating various data sources, such as epidemiological, healthcare, and socioeconomic data. The diversity and complexity of data involved in public health assessments are more pronounced compared to other policy evaluations. Additionally, due to the sensitive nature of health data, these evaluations must carefully address data privacy and ethical concerns to ensure individual rights and privacy are protected during data usage. With the advent of the digital economy, driven by the rise of the Internet, cloud computing, and artificial intelligence, many biological data and medical records have been digitized. This has introduced new types of data, such as text, image, and audio data, which are typically unstructured, high-dimensional, low in information density, and large in scale, exceeding the capabilities of traditional public health policy evaluation methods (4). Introducing machine learning methods is essential for effectively exploring and managing these data.

Machine learning is an emerging technology that integrates knowledge from diverse fields such as computer science, engineering, and statistics. It is widely utilized in areas including science, technology, and medicine, and is increasingly attracting interest from researchers in the social sciences (5). The advent of machine learning offers a novel approach to public health policy evaluation. By leveraging advanced algorithms and significant computational power, machine learning can extract critical insights from large datasets and develop more precise predictive models, thereby providing more reliable references for public health policy formulation. Currently, machine learning has become widely prevalent in social science research, leading to numerous review articles focusing on machine learning and causal relationships (6). For example, Grimmer (7), Varian (8), Guo et al. (9). Provide brief introductions to the fundamental concepts and logic of causal identification, explore the intersection of machine learning with causal identification, and discuss the potential of integrating machine learning models into causal identification processes. Mullainathan and Spiess (10), Guo and Tao (11) underscore the critical role of machine learning in causal identification within social sciences, while also addressing the novel challenges it introduces. The existing literature primarily explores the relationship between machine learning and causal identification and emphasizes the significance of incorporating machine learning methods for causal identification within the context of big data. This article, however, emphasizes the value of machine learning in public health policy effect evaluation. Related literature includes research by Shen et al. (12), who compare traditional policy evaluation methods such as the difference-in-differences method, synthetic control method, and panel data method with machine learning approaches, offering empirical researchers a guide for method selection. Nevertheless, this article differs significantly: Shen et al. (13) primarily introduce traditional and machine learning-based policy evaluation methods, conducting a detailed comparison for methodological selection. In contrast, this article delves into the limitations of traditional public health policy evaluation methods within the context of big data and provides a comprehensive exploration of expanding public health policy evaluation boundaries using machine learning methods. Unlike Shen et al.’s straightforward comparison, this article presents a more thorough and detailed examination of machine learning’s application in public health policy evaluation.

This study aims to address the following key question: How can machine learning techniques improve the evaluation of public health policies in the era of big data, and what challenges and solutions are associated with their application? Hence, the primary contributions of this paper are twofold: first, it outlines the challenges encountered by traditional public health policy effect assessment methods in the context of big data and highlights the advantages and significant value of machine learning in this field. It also offers new insights for scholars seeking to expand the applicability of public health policy effect assessment. Second, the article addresses the limitations of machine learning in public health policy effect assessment and suggests potential directions and efforts for the further development of public health policy assessment and machine learning. The structure of the remaining sections in this article is as follows: Section 2 introduces traditional methods of public health policy impact assessment and examines their challenges in the context of big data. Section 3 highlights the advantages and substantial value of machine learning in public health policy impact assessment within the realm of big data. Section 4 discusses the limitations of machine learning in public health policy impact assessment and proposes future directions. Finally, Section 5 provides a comprehensive summary of the entire paper.

2 Traditional methods of public health policy impact assessment and their existing issues 2.1 Traditional methods of public health policy assessment

The field of econometrics has developed several traditional methods for quantitatively analyzing public health policy effectiveness. Key among these are the difference-in-differences (DID), synthetic control method (SCM), and regression discontinuity design (RDD), which have gained prominence in academia and are extensively used across various public health policy domains. This section examines the principles, applicability, specific model configurations, and potential challenges related to these conventional public health policy evaluation methods.

2.1.1 Difference-in-difference (DID)

The difference-in-differences (DID) method, originally introduced by Card et al. in their study of minimum wage policy, has been widely adapted for use in public health policy evaluation (14). This method assesses the effects of public health interventions by comparing the differences in outcomes between treatment and control groups before and after a policy is implemented. The first step involves calculating the difference in health outcomes for individuals before and after the policy intervention, which helps control for individual fixed effects (unchanging characteristics specific to each individual). The second step takes a secondary difference, focusing on time-based differentiation across the treatment and control groups, which aims to eliminate time fixed effects (common factors that remain consistent over time). This approach is particularly valuable in public health when policies are tested in certain regions or populations before being rolled out more broadly. It provides a robust way to assess the impact of interventions by controlling for both individual and time-specific effects. However, public health policies implemented simultaneously across all regions may not be well-suited for the DID method. Generally, the model specification for DID in public health policy evaluation follows this structure:

Yit=β0+β1Treati+β2Postt+β3TreatiPostt+∑j=1JθjZijt+μi+δt+εit    (1)

In Equation (1), subscript i denotes the sample and t denotes time. Yit represents the dependent variable, indicating the outcome for sample i at time t . Treati is a dummy variable indicating whether the sample is subject to the public health policy intervention, assigned 1 if affected by the policy, otherwise 0. Postt is a dummy variable for the policy implementation time point, 0 before and 1 after implementation. The term TreatiPostt represents the interaction term in the difference-in-differences method, used to identify policy effects. If β3>0 , the policy increased Yit ; if β3<0 , it decreased Yit . Zijt is the matrix of control variables, including factors affecting the dependent variable. μi and δt are individual and time fixed effects, respectively. εit represents the random disturbance term.

Figure 1 demonstrates the application of the Difference-in-Differences (DID) methodology in evaluating public health policy interventions. It highlights changes in outcome variables, such as health expenditures and mortality rates, between treatment and control groups before and after the intervention. The observed parallel trends in the pre-intervention period confirm the validity of the DID approach, while the divergence in outcomes post-intervention quantifies the policy’s causal impact. By incorporating machine learning into this framework, the study enhances policy evaluation by capturing complex, non-linear relationships and systemic factors, such as hospital ownership. This integration establishes a robust empirical foundation for analyzing public health outcomes and assessing policy effects.

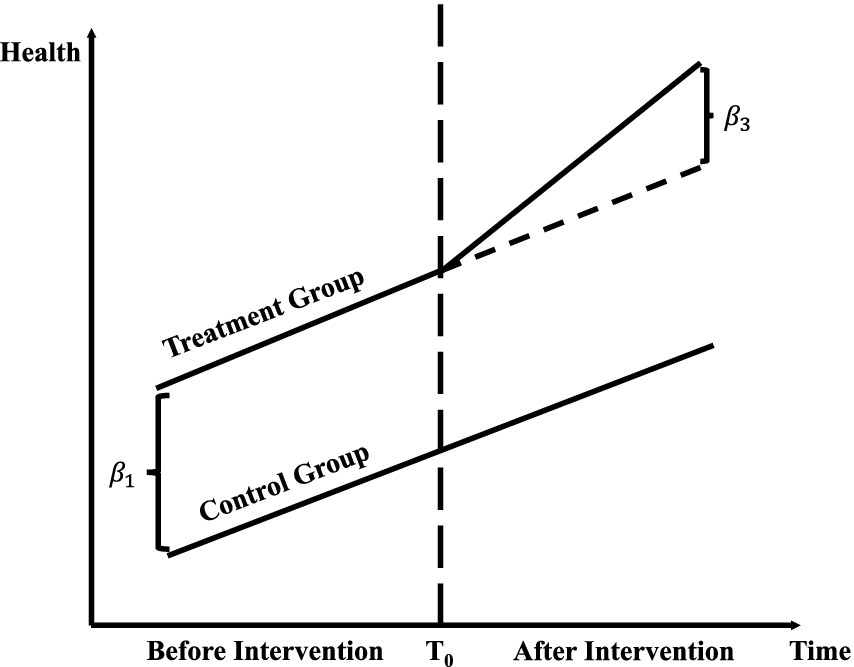
Figure 1. Difference-in-differences (DID) method.

The double-difference method may encounter challenges related to the parallel trend assumption and selection bias in evaluating public health policy effects. This method relies on the parallel trend assumption, which posits that the health trends of the treatment and control groups are parallel before and after the implementation of public health policies. However, fulfilling this assumption is often difficult in real-world evaluations, particularly when external health interventions or uncontrollable factors, such as epidemics, influence the policy implementation. If the parallel trend assumption is violated, it can result in significant bias in estimating policy effects, thereby compromising the accuracy and reliability of public health assessments. Additionally, the double-difference method is susceptible to selection bias. If, following the implementation of a public health policy, the differences between the treatment and control groups arise not only from the policy effects but are also influenced by other health-related factors (e.g., health infrastructure, access to medical services), the double-difference method may not accurately assess the actual effects of the policy, leading to distorted evaluation results.

In the context of big data and machine learning, the Difference-in-Differences (DID) method can be improved by incorporating machine learning algorithms, such as propensity score matching (PSM) or random forests, to construct balanced treatment and control groups that more effectively satisfy the parallel trends assumption. For instance, machine learning models can analyze high-dimensional datasets to identify key covariates influencing treatment assignment, thereby enhancing the robustness of DID analysis. Additionally, DID can be adapted to process unstructured data, such as social media health posts or electronic medical records, by employing natural language processing (NLP) or image recognition techniques, expanding its applicability in public health contexts.

2.1.2 Synthetic control method (SCM)

The synthetic control method (SCM) extends the double-difference method by serving as a counterfactual for the treatment group. In evaluating the effects of public health policies, it is often challenging to identify an optimal control group that closely matches the treatment group in all relevant aspects. SCM, based on the counterfactual estimation framework, offers a viable solution. The core idea is that, although it is difficult to find ideal control samples identical to the subjects undergoing policy intervention, a control group can be constructed by linearly combining weights from a pool of potential control groups. This synthetic control group can mirror the characteristics of the treatment group prior to policy implementation, ensuring that the predictor variables align with those of the treated sample. Consequently, it allows for a comparison of changes in health variables between the “real treatment group” and the “synthetic control group” before and after policy implementation, ultimately revealing the net effect of the public health policy (15). This approach is particularly suitable for public health policies with few pilot programs, as they may be tested in only one or two regions, making it difficult to find exact matches elsewhere. Thus, constructing a synthetic counterfactual reference group through an appropriate linear combination of non-pilot districts becomes essential. Typically, the synthetic control method follows four key steps:

Firstly, the model specification assumes an experimental group where the public health policy is implemented, and multiple control groups where the public health policy is not implemented. For each sample i and time t, the model is represented as follows:

Yit=β0+β1Treatit+∑j=1JθjZijt+μi+δt+εit    (2)

In Equation (2), Subscript i denotes the sample and t denotes time. Yit is the dependent variable, representing the outcome for sample i at time t . Treatit is a dummy variable indicating public health policy implementation, assigned 1 if the policy is implemented for sample i , and 0 otherwise. Zijt represents the matrix of control variables, including factors affecting the dependent variable. μi and δt denote individual and time fixed effects, respectively. εit represents the random disturbance term.

Secondly, the synthetic control group is constructed for each sample i where the public health policy is not implemented, by weighting and averaging observed data from other control group samples.

Yitŝ=∑j=1JWijYjt    (3)

In Equation (3), Yitŝ denotes the predicted value of the synthetic control group; j represents the number of reference samples used to construct the synthetic control group; Wij represents the weights computed for each reference sample j .

Thirdly, synthetic weights are determined by minimizing the differences observed between the experimental group and the synthetic control group before public health policy implementation.

min∑t=T0T1Yit−∑j=1JWijYjt2    (4)

In Equation (4), T0 and T1 denote the time points before and after public health policy implementation, respectively.

Fourthly, as shown in Equation (5), public health policy effects are estimated by comparing the observed values of the experimental group with the predicted values of the synthetic control group.

Policy Effects=Yit−Yitŝ    (5)

Figure 2 demonstrates the application of the synthetic control method (SCM) in the context of public policy evaluation. The x-axis represents the time period, while the y-axis indicates the outcome variable of health. The solid line depicts the actual observations for the treated unit, whereas the dashed line represents the estimated counterfactual outcomes generated by the synthetic control group. Before the intervention, marked by a vertical line, the treated unit and the synthetic control group exhibit a similar trajectory, confirming that the SCM effectively approximates the pre-intervention trend of the treated unit. After the intervention, a noticeable divergence between the two lines emerges, reflecting the treatment effect. This gap quantifies the impact of the intervention on the treated unit, assuming the synthetic control group serves as a valid counterfactual.

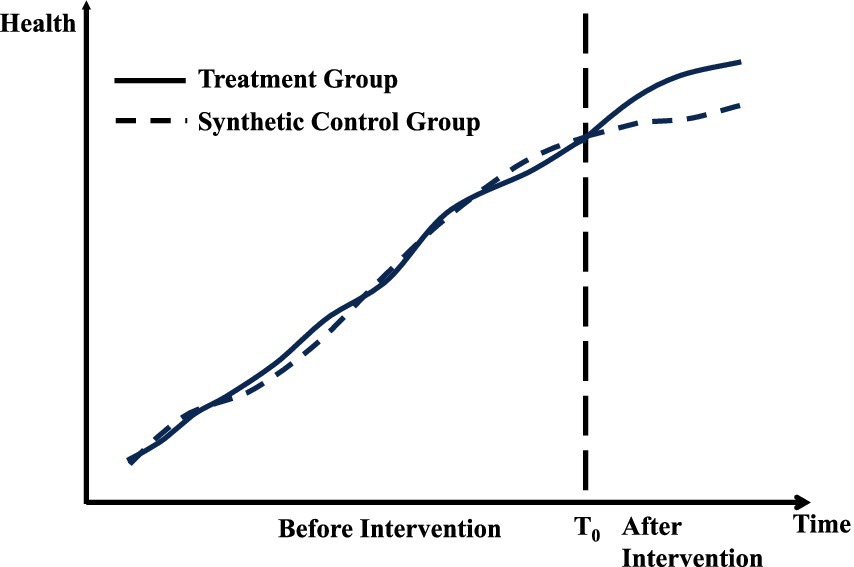
Figure 2. Synthetic control method.

The synthetic control method may encounter selection bias in public health policy evaluation due to synthetic portfolio construction. This method necessitates the creation of a synthetic portfolio to simulate the post-policy implementation scenario for comparison with the actual treatment group. However, the selection process may be influenced by the researcher’s subjective preferences and methodological choices, leading to biased outcomes. For instance, a researcher might favor synthetic combinations that demonstrate more favorable effects post-implementation or might rely on specific techniques or models while overlooking alternative methods that could be more suitable. Such subjective and technical decisions can yield synthetic combinations that do not accurately reflect the actual context and compromise the validity and reliability of the policy assessment. Furthermore, public health policies typically target unique intervention objectives and specific populations, making it challenging to identify an appropriate control group. This limitation further diminishes the objectivity and accuracy of the evaluation results. Consequently, the validity and applicability of the synthetic control method in public health policy evaluation are subject to significant constraints.

In the era of big data, machine learning algorithms, such as k-means clustering and neural networks, can automate the selection of control units, thereby minimizing subjectivity in the construction of synthetic portfolios. These algorithms detect patterns and similarities in large-scale datasets, facilitating the creation of more representative synthetic control groups. For instance, when evaluating a public health policy targeting specific regions, unsupervised learning techniques can group similar regions based on health indicators, socioeconomic variables, and other high-dimensional features, thereby enhancing the accuracy and credibility of synthetic control method (SCM) applications in public health.

2.1.3 Regression discontinuity design (RDD)

The regression discontinuity design (RDD) was initially proposed by Thistlewaite and Campbell (16), but it gained widespread attention and application in 2001 following Hahn et al.’s formal proof (17). Currently, RDD is extensively used by social science researchers to evaluate public health policies in non-experimental settings (18). The core idea is that when individual characteristics of a subgroup cross a specific policy threshold, the policy induces a discontinuity in the outcome variable. Near the discontinuous policy threshold, groups on both sides form “comparable” experimental and control groups. Given the similarity of these groups, any disparities in the outcome variable are solely attributable to the policy intervention. The breakpoint regression model is ideal for “one-size-fits-all” policies that necessitate explicit policy thresholds, where entities must surpass (or fall below) these thresholds to fall under the policy’s purview. Typically, breakpoint regression models are structured as follows:

Yit=γ0+γ1Xit−c+γ2Dit+γ3Xit−c•Dit+∑j=1JθjZijt+μi+δt+εit    (6)

In Equation (6), subscript i denotes the sample and t denotes time. Yit is the dependent variable indicating the outcome for sample i at time t . Xit represents the continuous variable related to the public health policy observed for individual i at time t . c denotes the public health policy threshold location. Dit is an indicator variable, equaling 1 when Xit exceeds c and 0 otherwise. γ1 is the coefficient of Xit , reflecting the slope near the public health policy threshold. γ2 is the coefficient of Dit , indicating the public health policy effect on the outcome variable. γ3 represents the coefficient of the interaction term capturing the discontinuity effect due to the public health policy. Zijt is a matrix of control variables affecting the dependent variable. μi and δt denote individual and time fixed effects, respectively. εit represents the random disturbance term.

Figure 3 demonstrates the central concept of regression discontinuity design (RDD) by depicting the relationship between the running variable (x-axis) and the outcome variable (y-axis). The graph features two fitted lines, each representing observations on either side of the threshold, marked by a vertical dashed line. The left segment corresponds to the control group, while the right segment represents the treatment group. At the threshold, the discontinuity, or “jump,” in the outcome variable indicates the causal effect of the treatment, provided the model’s validity conditions are satisfied. The curvature in the fitted lines reflects non-linear relationships in the data, which are addressed through the chosen modeling strategy, such as higher-order polynomials or machine learning algorithms.

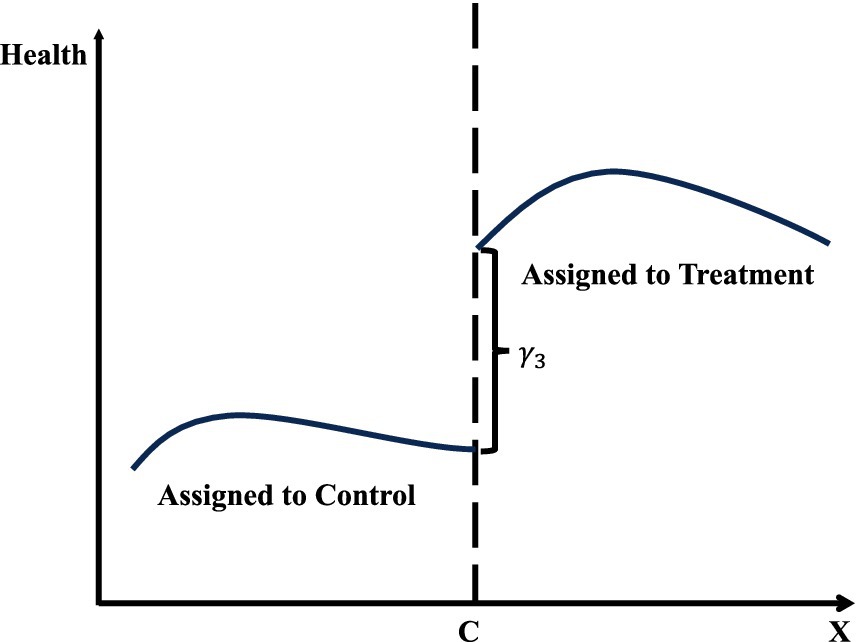
Figure 3. Regression discontinuity design (RDD).

Regression discontinuity design may suffer from breakpoint selection bias in public health policy evaluation. The core of this model relies on a predetermined breakpoint to distinguish between treatment and control groups. However, the selection of breakpoints can be influenced by the researcher’s subjective preferences or external factors, leading to inappropriate or inaccurate choices. In public health policy, breakpoints may be unclear and challenging to define. If a researcher arbitrarily selects a breakpoint without adequate justification, it can result in significant bias in the assessment results, thereby affecting the accurate evaluation and interpretation of policy effects. For instance, a researcher might search for the most optimal breakpoints in the data or choose different breakpoints before and after the implementation of the policy to obtain more favorable results. Such subjectivity and flexibility in breakpoint selection may compromise the objectivity and credibility of the assessment outcomes. Additionally, regression discontinuity design relies on the uniform distribution of the sample on both sides of the cutoff point. If the sample size is insufficient or if there is systematic selection bias on either side of the cutoff, the reliability of the assessment results may be further weakened.

In the context of big data and machine learning, Regression Discontinuity Design (RDD) can be enhanced by leveraging algorithms such as gradient boosting or support vector machines to identify breakpoints more objectively. These methods analyze high-dimensional datasets to detect natural thresholds or discontinuities in the data, thereby reducing reliance on arbitrary or subjective breakpoint selection. Additionally, RDD can be extended to fuzzy designs using machine learning techniques to predict treatment probabilities when treatment assignment is not perfectly determined by the threshold. For example, in a vaccination program study, machine learning models can estimate individual-level probabilities of receiving treatment near the threshold, thereby enhancing the robustness of RDD analysis.

2.2 The problems of traditional public health policy assessment methods in the context of big data

The information technology revolution, driven by the Internet, cloud computing, and artificial intelligence, has facilitated the widespread adoption of digital technology in public health. Many aspects of human health behavior and medical activities are now digitally recorded, resulting in vast amounts of new data that encompass dynamic information on individual health status and healthcare service usage. These data are interrelated in complex ways (19), and traditional public health policy evaluation methods are often insufficient for processing and analyzing such complex datasets (20).

2.2.1 Unstructured data challenges and huge volume difficulties

Unstructured data in the era of big data presents new challenges for public health policy evaluation. Traditional assessments primarily rely on structured data, such as health statistics yearbooks, medical record databases, or field surveys, which have clear formats and fixed fields, making them easier to analyze and model. However, with the rapid advancement of computer information technologies like the Internet, cloud computing, and artificial intelligence, unprecedented and diverse data types—such as text, images, and audio—are now available, posing challenges for traditional public health evaluations (21). Big data is characterized by unstructured formats, high dimensionality, and low information density (22), creating complexity for traditional evaluation methods. Unstructured data, including electronic medical records, health monitoring data, and social media health information, differs from structured data in its flexibility and diversity. Traditional methods are ill-equipped to extract and analyze such data. High dimensionality involves numerous features and attributes, such as individual health behaviors and environmental factors, exceeding the capacity of traditional tools. Moreover, big data’s low information density requires sophisticated techniques to extract meaningful insights, making manual analysis insufficient for processing high-noise data. Additionally, the sheer volume of big data poses significant challenges in terms of storage, transmission, and processing (23). Public health policy evaluation often necessitates the integration of data from multiple domains, such as medical, social, and environmental sources. This may involve merging multiple large databases, which traditional computing methods handle inefficiently. Thus, advanced technologies like parallel computing and distributed storage are essential for efficiently processing large-scale data and ensuring the accuracy and timeliness of public health policy evaluations.

2.2.2 Model specification issues 2.2.2.1 Misspecification issue

Quantitative empirical research on public health policy assessment can be categorized into two types: theory-driven and data-driven approaches. Theory-driven research, which traditionally dominates this field, constructs low-dimensional parametric models based on public health theories. However, these theories are often derived from mathematical models built on numerous assumptions, aiming to simplify and abstract complex health systems. This method focuses on identifying causal relationships between key health indicators and policy interventions to reveal the intrinsic effects of policies on health outcomes. The advantages of the theory-driven approach lie in its model simplicity, ease of understanding, and straightforward result interpretation. In macroeconomics, the Lucas Critique illustrates how dynamic, theory-driven models integrate rational expectations to improve predictions of policy impacts, thereby avoiding the limitations of purely data-driven models. Similarly, in psychology, cognitive behavioral therapy (CBT) utilizes behavioral theories to explain the interaction between cognitive distortions and behavioral outcomes, offering a structured and interpretable framework for clinical interventions. These examples highlight the strength of theory-driven approaches in promoting deeper understanding and more effective application of models. However, its limitations stem from reliance on a priori knowledge and theoretical assumptions. Model construction depends on the researcher’s prior understanding of the health problem and domain knowledge, making it difficult to handle complex big data. This approach may overlook the intricate relationships and nonlinear patterns present in large datasets. Consequently, theory-driven models may struggle to capture deeper insights in high-dimensional health data, leading to potential model misspecification and impeding accurate public health policy evaluation (4).

2.2.2.2 Multicollinearity issue

In the era of big data, public health datasets contain numerous variables, resulting in high-dimensional data. This increase in dimensionality amplifies the correlation between variables, heightening the risk of multicollinearity, which threatens both the accuracy and interpretability of models (24). Multicollinearity arises from the interrelationships between health-related variables within large datasets. Big data encompasses vast and complex information across multiple domains, including individual health status, socioeconomic factors, and environmental conditions. Traditional methods for evaluating public health policies struggle to identify correlations among variables within such large-scale data, potentially leading to multicollinearity. This complicates the accurate estimation of independent contributions from variables in traditional models, resulting in unstable and unreliable coefficient estimates, which can even lead to incorrect evaluations of public health policies, ultimately undermining the scientific rigor and effectiveness of policy decisions.

2.2.2.3 Overfitting issue

Traditional models for assessing the effects of public health policies typically involve low-dimensional explanatory variables and unknown parameters. Researchers primarily focus on consistently estimating these unknown parameters and assessing the statistical significance of their estimates using the t-statistic or p-value, thus inferring their actual impact on health outcomes. For instance, when the t-statistic exceeds its critical value, researchers may reject the null hypothesis (commonly the hypothesis that the parameter equals zero) in favor of the alternative hypothesis, concluding that the parameter estimate is statistically significant and has a meaningful impact on public health. However, in the context of big data, large sample sizes often result in parameter estimates closely aligning with true values or their probability limits, accompanied by small standard errors. Consequently, even when true parameter values are near zero and their actual impact on health outcomes is minimal, the t-values may still achieve statistical significance, raising concerns about overfitting. Therefore, while the distinction between statistical significance and actual significance of public health effects is less critical with smaller data volumes, it becomes essential to differentiate between the two in big data contexts (4). Otherwise, a parameter deemed statistically significant may not possess sufficient actual impact on public health to support substantive policy conclusions.

3 The advantages of machine learning in public health policy impact assessment

Big data, characterized by unstructured formats, high dimensionality, low information density, and large volumes, poses significant challenges for traditional public health policy evaluation methods. Issues such as model misspecification, multicollinearity, and overfitting are increasingly prominent in this context. Machine learning offers a solution to these challenges by flexibly handling large-scale, high-dimensional health data, uncovering hidden associations, identifying nonlinear relationships, and reducing dependence on a priori knowledge through automatic feature extraction.

3.1 Addressing challenges of unstructured data and massive volume

In the era of big data, machine learning offers a flexible and adaptive tool to address the challenges posed by unstructured data in public health policy evaluation. Machine learning is particularly effective in handling unstructured, high-dimensional, and low-information-density data. For unstructured health data, such as text, images, and audio from sources like consultation records and medical imaging, machine learning—particularly deep learning models—leverages its capability to process unstructured information. These models comprehensively analyze textual health content, recognize patterns in medical images, and interpret audio data, thereby extracting diverse health-related insights and aiding in the deeper analysis of public health policy effects (25). Machine learning algorithms also manage high-dimensional health data by utilizing techniques like feature selection and dimensionality reduction, enabling automatic identification of key features linked to policy effects and alleviating the burden of dimensionality on traditional methods (26). Additionally, machine learning excels at extracting valuable information from noisy health data, where traditional methods struggle, improving both the efficiency and accuracy of data analysis. Furthermore, machine learning addresses the challenges of storing, transmitting, and processing large-scale health data using advanced technologies such as parallel computing and distributed storage. Parallel computing allows for the simultaneous execution of multiple tasks, boosting computational efficiency, while distributed storage enables the decentralized management of large datasets across multiple nodes, enhancing data access speed and overall processing capacity. These technologies make machine learning models more efficient in handling large-scale health data, meeting the real-time and precision demands of public health policy evaluation. In summary, machine learning algorithms provide a comprehensive approach to extracting and analyzing big health data, offering policymakers more accurate and reliable assessments of public health policy effects.

3.2 Addressing issues in traditional public health policy evaluation models 3.2.1 Data-driven solutions to address mis-specification issues

Machine learning mitigates the risk of model mis-specification in public health policy evaluation through a data-driven approach. Traditional modeling often relies on specific theoretical frameworks that may simplify actual conditions. As a result, it typically employs linear models, such as linear regression, which assume a linear relationship between variables. However, these assumptions may be overly simplistic and fail to accurately capture the potential nonlinearities and interactions among variables when applied to complex public health phenomena in the context of big data and heterogeneity. Furthermore, manually incorporating these relationships can lead to model mis-specification, biasing the estimated parameters. In contrast, machine learning algorithms, such as decision trees and support vector machines, effectively capture nonlinear relationships without the risk of biased estimates resulting from model mis-specification (27, 28). Additionally, ensemble algorithms in machine learning, such as Super Learner, Bayesian Stacked Regression Trees, and Deep Learning, are designed to optimize model specification. These algorithms utilize foundational models trained independently on the same samples, leveraging relatively weak learning models and subsequently integrating their results for improved generalization. By evaluating the strengths of each model, ensemble algorithms aim to identify the optimal model, thereby significantly reducing the risk of mis-specification. This approach provides researchers with more flexible and adaptable tools for understanding and interpreting patterns and associations in large-scale health data, ultimately enhancing the accuracy and reliability of public health policy effect assessments.

3.2.2 Dimensionality reduction of high-dimensional models resolves multicollinearity issues

Dimensionality reduction in high-dimensional models is an effective strategy for addressing multicollinearity issues in the assessment of public health policy effects. Reducing the number of variables in the model decreases correlations between them, thereby improving the stability and interpretability of the model. The primary objective of dimensionality reduction in high-dimensional models is to preserve essential information while eliminating redundant dimensions, aiming for a more concise and interpretable model. Common dimensionality reduction methods include Principal Component Analysis (PCA), Singular Value Decomposition (SVD), and other techniques. These methods transform the original explanatory variables through linear transformations to produce a new set of variables known as principal components. These principal components are linear combinations of the original variables designed to preserve as much variance from the original data as possible. Selecting a subset of principal components enables dimensionality reduction of the original high-dimensional data, thereby reducing the number of explanatory variables in the model and mitigating multicollinearity issues. Multicollinearity arises from high correlations between variables, and principal components are typically constructed by identifying directions of maximum variance, making them orthogonal to each other. This orthogonality implies that correlations between variables are significantly reduced in the space of principal components, thereby mitigating the impact of multicollinearity (29). Selecting principal components allows us to focus on the most representative directions in the public health data, condensing the information of the original data into fewer dimensions. This approach captures the essential characteristics of the data more effectively. However, it is crucial to carefully select the number of principal components to retain during dimensionality reduction. Choosing too few components may lead to loss of important information, while selecting too many may not effectively reduce dimensionality. A common method is to determine the number of principal components based on the cumulative contribution of explained variance (30). Typically, the number of principal components chosen achieves a cumulative contribution rate above a certain threshold, ensuring sufficient information retention while reducing dimensionality.

3.2.3 Regularization addresses overfitting problems

Regularization mitigates model complexity by introducing a penalty term into the model’s loss function of the public health policy effects assessment model, thereby preventing overfitting to the training data and enhancing its generalization ability on unseen data. The central concept of regularization is to balance the model’s fit and complexity to avoid overfitting. The most commonly used regularization methods are L1 regularization (Lasso) and L2 regularization (Ridge) (31). L1 regularization sparsifies the model by incorporating the L1 norm of the parameter vectors into the loss function. This approach drives some model coefficients to zero, thereby reducing the impact of less important features. Conversely, L2 regularization encourages smaller coefficient values by adding the L2 norm of the parameter vectors to the loss function. This effectively controls the model’s weight size and mitigates overfitting to noise. Additionally, regularization is manifested through the penalty term in the model. This term modifies the model’s loss function to ensure that the model not only fits the training data well but also keeps its parameters within a reasonable range. Consequently, the model emphasizes capturing the essential patterns in the public health data while minimizing overfitting to noise. The strength of regularization is controlled by a tuning parameter, which, when adjusted, helps strike a balance between model complexity and fit.

4 Applying machine learning for public health policy evaluation 4.1 Application steps

Machine learning has emerged as a powerful tool for evaluating policy effectiveness in the context of big data, addressing limitations associated with traditional methods. Using text data as an illustrative example, this article explores the application of machine learning in policy evaluation, focusing on critical steps such as data preparation and cleaning, model selection, training and tuning, model interpretation, and result analysis. The objective is to assist researchers in effectively utilizing this advanced methodology.

4.1.1 Data preparation and cleaning

The process of preparing and cleaning data for machine learning begins with text data mining. Natural language processing (NLP) techniques, such as word vectors and bag-of-words models, are employed to analyze text structure and semantics, extracting key information to generate meaningful features for subsequent processing. The next step addresses missing and outlier data through techniques like random forests and k-nearest neighbors for predicting and imputing missing values. Outlier detection methods, including isolation forests and One-Class SVM, are applied to identify and manage anomalies, thereby enhancing data quality. Data smoothing and transformation follow, utilizing approaches like moving averages and exponential smoothing to stabilize time series data, reduce noise, and improve interpretability. Subsequently, feature engineering techniques, such as principal component analysis (PCA) and feature selection methods (e.g., variance thresholding), are employed to extract critical features, optimizing model inputs and improving generalization. The final step standardizes and normalizes data using techniques such as Z-score standardization and MinMax normalization, ensuring consistent feature scales to mitigate bias and provide stable inputs for model training.

4.1.2 Model selection, training and tuning

After data processing and cleaning, the next critical step is model selection, training, and tuning, which significantly impacts model performance. The initial phase involves selecting candidate models, such as decision trees, support vector machines, random forests, linear regression, logistic regression, k-nearest neighbors, naïve Bayes, and neural networks, to encompass diverse modeling approaches. Unlike traditional methods, this process integrates data-driven strategies with domain expertise and policy theories, fostering the development of interpretable and credible models. Model training and hyperparameter tuning then proceed, using cross-validation techniques like k-fold cross-validation to partition the dataset into training and validation sets. Techniques such as grid search, random search, Bayesian optimization, genetic algorithms, gradient boosting, and automated machine learning (AutoML) are employed to identify optimal hyperparameter configurations, guided by policy considerations. These configurations are selected based on validation set performance. Subsequently, model comparison and selection evaluate metrics like accuracy, precision, F1 score, AUC-ROC curves, and confusion matrices to identify the best-performing model. This evaluation integrates domain knowledge, ensuring alignment with broader policy objectives. Finally, ensemble learning techniques, including voting classifiers, stacked models, random forests, gradient boosting trees, and deep learning ensembles, are employed to enhance generalization capabilities. The finalized model is validated using an independent test set to ensure robust performance on unseen data. The models available for each step are shown in Table 1.

Table 1. Models available for model selection, training and tuning.

4.1.3 Model interpretation and results analysis

After the processes of model selection, training, and tuning, it is essential to interpret the final model and its outcomes using robust methodological tools. Local interpretability analysis, for instance, employs techniques like Local Interpretable Model-Agnostic Explanations (LIME). LIME constructs interpretable surrogate models for specific samples, allowing researchers to identify key factors—such as vaccination rates, hospital accessibility, or community outreach programs—that significantly influence the classification of public health interventions as “effective” or “ineffective.” This approach facilitates a nuanced understanding of decision-making in individual cases, such as assessing the effectiveness of a vaccination campaign in a particular region.

Global interpretability analysis utilizes Shapley Additive Explanations (SHAP) values to quantify the contribution of each feature across the entire dataset. In evaluating public health policies, SHAP values provide insights into how variables such as healthcare expenditure, population density, and disease prevalence influence model predictions. For example, a SHAP summary plot might demonstrate that higher healthcare expenditure consistently correlates with improved health outcomes, whereas the impact of population density varies depending on regional infrastructure.

To complement these analyses, causal model visualization is used to illustrate the pathways and interactions between policy interventions and health outcomes. Directed acyclic graphs (DAGs) enable researchers to explicitly map the relationships between public health interventions, such as mask mandates or quarantine measures, and their effects on outcomes like infection rates or mortality. For instance, a DAG might show how increasing testing capacity reduces disease transmission through early detection and isolation, aligning the model’s predictions with epidemiological theory.

Model evaluation and validation are crucial for ensuring that interpretability results align with theoretical expectations and public health frameworks. These results are subsequently tested on an independent dataset to evaluate the model’s performance on unseen data, thereby confirming its robustness in predicting policy effectiveness across diverse settings.

Counterfactual analysis is a vital component of public health policy evaluation, enabling the exploration of hypothetical scenarios. For instance, the model can simulate potential outcomes if a lockdown policy had not been implemented during a pandemic, helping researchers assess the policy’s direct and indirect effects on public health metrics such as infection rates, hospital admissions, and fatalities. This approach strengthens the model’s capacity to generate actionable insights for policymakers and public health officials. Figure 4 outlines the steps involved in applying machine learning to public health policy evaluation.