1 Introduction

Listening is a biological process that engages the entire auditory system. The process, from sound pressures to neural activations, includes (non-linear) transforms of the peripheral auditory system as well as complex processing within the central auditory system. The listening process also affects the electrical activity of the brain, which can be measured on scalp-level using electroencephalography (EEG). Linear filter estimation, referred to as temporal response functions (TRFs) (Crosse et al., 2016; Alickovic et al., 2019; Geirnaert et al., 2021), has been shown to capture the relations between the auditory system and EEG signatures (O'sullivan et al., 2015). State-of-the art methods employ TRFs to analyze phonemes (Di Liberto et al., 2015; Brodbeck et al., 2018; Carta et al., 2023) and semantic content (Broderick et al., 2018; Gillis et al., 2021). The TRF methods are also particularly valuable for decoding auditory attention, specifically in identifying the attended talker from EEG signals in challenging listening situations like cocktail-party environments (Cherry, 1953). Effectively decoding auditory attention to distinguish and enhance attended speech in multi-talker situations holds significance for hearing aid (HA) applications (Lunner et al., 2020; Alickovic et al., 2020, 2021; Andersen et al., 2021).

The mentioned studies, along with others, provide evidence that neural speech processing exhibits a linear component. Specifically, there are robust linear relationships between the speech envelope and the concurrent EEG signatures. Hence, spectral coherence analysis between the speech envelope and EEG signals can confidently identify and analyze the underlying system to a significant degree, as demonstrated in Viswanathan et al. (2019) and Vander Ghinst et al. (2021). Spectral coherence is also a measure of the linear coupling between two signals, calculated as the cross-spectrum normalized by the respective auto-spectrum of both signals.

Various methods exist for estimating spectral coherence, where the Welch method is the most commonly applied. In this approach, uncorrelated Fourier-based spectrum estimates from multiple data segments (that may overlap) are averaged (Welch, 1967). Another state-of-the-art approach is Thomson's multitaper method, which multiplies data with various tapering windows before Fourier analysis and subsequent averaging (Thomson, 1982; Walden, 2000; Karnik et al., 2022). Multitapers are often applied in various applications for robust spectral estimation of EEG (Alickovic et al., 2023; Reinhold and Sandsten, 2022; Viswanathan et al., 2019; Babadi and Brown, 2014; Hansson-Sandsten, 2010).

The statistics in coherence estimation using Welch method (Carter and Nuttall, 1972; Carter et al., 1973) as well as the Thomson's multitaper method (Thomson, 1982; Bronez, 1992; McCoy et al., 1998; Brynolfsson and Hansson-Sandsten, 2014; Hansson-Sandsten, 2011) has been thoroughly studied. The coherence of 1 signifies a perfect linear connection between signals, while no coupling yields the ideal coherence is 0. In practice, the lack of infinite data always introduces a significant bias upwards toward positive values in the no coupling case (Carter and Nuttall, 1972). In comparison, the variance can be assumed to be small when a reasonable amount of data is available (Carter et al., 1973; Thomson, 1982).

This paper introduces a new method for EEG-speech envelope coherence estimation, denoted bias-reduced coherence (BRC). The method aims to decrease the bias of estimation, while assessing the effectiveness of coherence in analyzing the relationship between speech envelope and EEG responses. With a certain choice in the cross-spectra estimation, as part of the coherence measure, the bias at low linear coupling can be reduced compared to traditional methods. Considering that EEG responses are susceptible to random noise, any detected linear coupling is expected to be weak. Real data is employed to evaluate the coherence methods and showcase their potential in decoding auditory attention. Furthermore, since coherence is applied to signals influenced by 1/f spectrally shaped noise prevalent in EEG data (Bénar et al., 2019), this study also investigates biases arising from this phenomenon. Coherence “levels out” the slanted noise in the coherence spectrum, and peaks that are widened by the taper kernel will have a bias toward higher frequencies. This paper quantitatively analyzes this bias and its implications for EEG and hearing application. The study's hypotheses are as follows.

Two types of anticipated biases in speech-EEG coherence estimation

1. Due to the high level of noise present in EEG data, we anticipate an overall upward bias across all frequencies from all methods. We propose that the new BRC can mitigate this bias, due to including taper phase information.

2. We expect coherence peaks from all coherence estimates to shift toward higher frequencies, due to the slanted nature of EEG noise. The extent and nature of this shift is hypothesized to be dependent on factors such as the number of tapers, data length, and the shape and power of the noise present in signals.

Auditory attention and hearing aid effects manifested in speech-EEG coherence changes

1. Differences in speech-EEG coherence between attended and ignored speech, specifically within the delta, theta, and alpha frequency bands associated with auditory processing, are anticipated when applying these methods to a population using HAs. For these bands, we expect clearer distinctions in coherence estimates with the BRC, since this improves bias and variance of coherence estimates.

2. Speech-EEG coherence differences are expected to be larger when HA noise reduction feature is activated compared to when it is deactivated.

This work extends our previous study (Keding et al., 2023), which introduces the novel BRC method that utilizes more of the phase information from tapered data segments. In Keding et al. (2023) the case when coherent signals are affected heavily by noise (causing low expected true coherence levels) is analyzed. Also, the base-level biases are compared for the traditional and the new BRC method, showing lower bias for BRC. Here, we present further analytical analysis of aspects evident during application of coherence as a measure within EEG analysis, focusing on neural speech tracking. Further comparisons of coherence methods topographically over channels are provided. Additionally, we investigate coherence as a metric for objectively assessing the effect of HAs on auditory attention during listening tasks.

The paper is structured as follows. Firstly, the traditional coherence method and the BRC are presented in Section 2, where the reduction in upward magnitude bias of BRC is explained. Analysis of the positional bias of peaks in the coherence spectrum due to 1/f noise is evaluated analytically as well as in simulations. Section 3 outlines the experimental design, pre-processing of data and statistical methods used in real data analysis. Results on real data are presented in Section 4, with related discussion in Section 5, highlighting the capabilities and limitations of coherence methods in auditory attention decoding and in objective evaluation of HA benefits. Conclusions are found in Section 6.

2 Coherence estimation

Spectral coherence Cxy(f) is the measure of the magnitude of a linear coupling between two signals in a system, ranging 0 ≤ Cxy(f) ≤ 1, here defined by its squared form

Cxy(f)=Sxy(f)2Sxx(f)Syy(f)    (1)

Sxy(f) is the cross-amplitude spectrum between signals x(n) and y(n). Sxx(f) and Syy(f) are the respective auto-spectra. Coherence, as denoted in Equation 1, is referred to as Magnitude Squared Coherence (MSC).

2.1 Magnitude squared coherence

Estimating the MSC entails estimating the different spectra according to

C^xy(f)=S^xy(f)2S^xx(f)S^yy(f)    (2)

The auto-spectra are estimated through averaging sub-spectra for each pair of L number of data segments and K number of data tapers as

S^xx(f)=1KL∑k=1K∑l=1LXk,l(f)Xk,l(f)*    (2) S^yy(f)=1KL∑k=1K∑l=1LYk,l(f)Yk,l(f)*    (4)

where Fourier transforms of the l:th data segments xl(n), yl(n) over time samples n and total lengths N, and k:th tapering window hk(t) of respective signal are

Xk,l(f)=∑n=0N-1xl(n)hk(n)e-i2πfn    (5)  Yk,l(f)=∑n=0N-1yl(n)hk(n)e-i2πfn    (6)

where i is the imaginary unit.

There are multiple options when constructing the cross-spectra from sub-spectra. Here we will consider two such options. The first has been used in Viswanathan et al. (2019) in speech envelope to EEG coherence estimation

S^xyTRAD(f)=1KL∑k=1K|∑l=1LXk,l(f)Yk,l(f)*|    (7)

Coherence estimation using this method is denoted the traditional method. In Equation 7 and from now on in the paper, the L data segments are assumed non-overlapping. A second option was introduced in our previous work (Keding et al., 2023), where both sums are taken before the absolute value as

S^xyBRC(f)=1KL|∑k=1K∑l=1LXk,l(f)Yk,l(f)*|    (8)

Note that these two options gives the same auto-spectra, since all sub-spectra are real and positive. The resulting estimator of coherence with S^xyBRC(f) is shown to decrease the bias upwards in magnitude for low coherence scenarios. This due to the traditional method averaging power over tapers without taking the phase information of tapers into account, which BRC does. This is shown in Keding et al. (2023). Coherence estimation using this method is therefore denoted bias-reduced coherence (BRC). The method in Equation 8 utilizes the phase information of the signals in estimation of the final cross-spectrum. A third option where the order of sums in Equation 7 is reversed, so absolute values of the sum of tapers are taken, is not considered here as L>K in most applications.

A common choice, in accordance with the Thomson's multitaper method, for the set of tapering windows 1, ..., K are the Discrete Prolate Spheroidal Sequences (DPSS), which can be seen in time and frequency domain in Figure 1 (Slepian, 1978). These are the windows that maximize the main lobe (or within-band) power relative to broadband power for a normalized frequency bandwidth W, but have no closed-form expression. They have been shown to have effective variance-reduction characteristics. Although it is argued here that these are suitable choices for tapering windows, the tapering windows can be chosen from another set, with the general methodology staying identical.

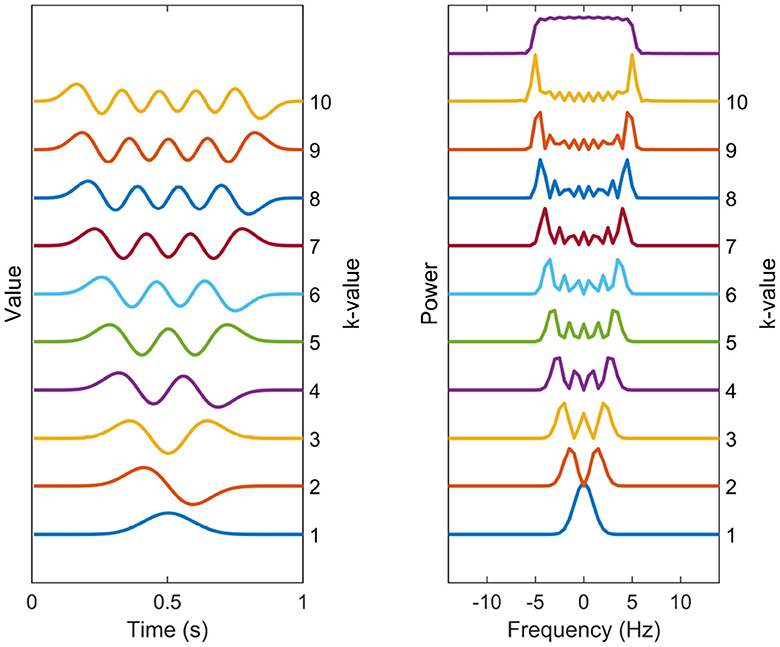
Figure 1. Spectral estimation windows. The temporal representation and power spectra of each of the 10 first DPSS windows used in the multitaper coherence estimation. The tapers are enumerated from bottom to top. The sum of the taper kernels is shown above the separate spectral kernels, effectively showing the width of the narrowband leakage effects.

The number of DPSS windows theoretically can be infinite, but using a large amount of tapering windows is not advisable due to its potential to significantly increase the narrowband leakage. This leads to the smearing of the spectrum, making spectral peaks of neighboring frequencies to be indistinguishable from one another. This phenomenon become particularly problematic when estimating coherence in 1/f-shaped noise, as discussed in Section 2.2. Instead, a practical approach involves selecting the desired bandwidth of the tapering windows according to the specific application and limit the number of windows accordingly. The DPSS windows are defined in terms of both their shape and the number of windows required to achieve this bandwidth. A common choice for the number of windows is K = 2NW, where N is the lengths of signals and W is the normalized frequency bandwidth.

A overall bias analysis of the traditional coherence estimation technique, compared to the BRC has been given in Keding et al. (2023). In this work, the BRC was shown to significantly reduce the bias of the coherence estimate level when there is no phase-locking between signals in channel x and y. The traditional method wrongly shows a peak in the coherence spectrum even though there is no phase-locking present. If 1/f-shaped noise is added to the phase-locked signal in either or both channels, the peaks of coherence for narrowband signals are also spectrally shifted toward higher frequencies. This simple observation made in Keding et al. (2023) is further expanded and analyzed in the following section.

2.2 Spectral positional bias in EEG-like noise

In various EEG-related applications, coherence measures are employed to analyze coherence spectra between EEG channels, or between EEG channels and sensory stimuli. This analysis allows the detection of key frequencies showing notable correlation. The identification of these specific correlation frequencies finds applications in tasks like filtering, denoising, and drawing functional insights about the brain.

However, a common challenge faced in visually inspecting the coherence spectra, or any coherence method based on the Fourier transform, is to identify key frequencies in the correlation between channels in the presence of unwanted spectral shifting of relevant coherence energy peaks. This shift is attributed to the presence of slanted 1/f noise, indicative of irrelevant brain activity. As the coherence normalizes the base levels of spectrum, the 1/f pattern becomes flattened, making it difficult to perceive its impact during peak analysis. This effect is particularly pronounced at lower frequencies, where the 1/f noise spectrum exhibits the most prominent degree of gradient.

2.2.1 Approximate coherence for sinusoidal signal

To illustrate the positional bias of peaks in the coherence spectrum when one or more signals are disturbed by 1/f noise, we introduce an expression for the coherence of a single frequency coupled model. Although the positional bias impacts any peaked spectra similarly, a simple case showing the bias involves single frequency oscillations is:

x(n)=s(n),  y(n)=s(n)+σpep(n)    (9)

where the signal s(n)=Ff→n[δf0(f)] represents a complex sinusoidal and the noise has a spectral distribution E[|Fn→f[ep(n)]|2]=1/fα, α>0.

In this subsection, it is assumed that Htot(f)=∑k=1K|Hk(f)|2=rect(f/B), the combined taper kernel, is a box function of energy one and frequency range of B = 2Wfs, as shown in Thomson (1982), where fs denotes the sampling frequency. The expected value of MSC between x and y can be approximated by the ratio of smeared cross-spectra and smeared auto-spectra of signals, since these are the expectations of the cross/auto-spectra. This gives a fairly simple expression for the final expectation of the coherence estimate. For f>B/2, an initial application of a zero:th order Taylor expansion of the expectation yields

E[C^xy(f)]≈|E[S^xy(f)]|2E[S^xx(f)]E[S^yy(f)]    (10) =|E[Sxy(f)]*Htot(f)|2(E[Sxx(f)]*Htot(f))(E[Syy(f)]*Htot(f))    (11) =|δf0(f)*Htot(f)|2(δf0(f)*Htot(f))((δf0(f)+σp2fα)*Htot(f))    (12) =Htot(f-f0)Htot(f-f0)+σp2fα*Htot(f)    (13) ={11+σp2fα*Htot(f)f∈[f0−B2,f0+B2]0 otherwise    (14)

where

1fα*Htot(f)=∫−B/2B/2(ν−f)−αdν=    (15) ={1−α+1((f+B/2)−α+1−(f−B/2)−α+1)α<1log(f+B/2)−log(f−B/2)α=11−α+1((f+B/2)−α+1−(f−B/2)