1. Introduction

The dynamics and functionality of neural networks, both artificial and biological, are strongly influenced by the configuration of synaptic weights and the architecture of connections. The ability of a network to modify synaptic weights plays a central role in learning and memory. Networks in cortical areas and in the hippocampus are believed to store patterns of activity through synaptic plasticity, making possible their retrieval at a later stage, or equivalently the replay of past network states (Citri and Malenka, 2008; Carrillo-Reid et al., 2016). Autoassociative neural networks have emerged as crucial models to describe this mode of computation by means of attractor dynamics. Memories can be thought of as attractor states that arise as a consequence of configuring synaptic weights following a Hebbian learning rule, where the synapse between two neurons is strengthened or weakened depending on how correlated is their activity (Hopfield, 1982).

A second, less explored way in which interactions between neurons in autoassociative memories can be modified is by adding or deleting connections. Evidence suggests that topological characteristics of biological neural networks are far from random, and might result from a trade-off between energy consumption minimization and performance maximization (Bullmore and Sporns, 2012). Over the course of evolution, what is now the human brain grew by several orders of magnitude in terms of the number of neurons (N), but the number of connections per neuron (c) has remained rather stable (Assaf et al., 2020). A limitation for increasing c is the scaling of the volume and mass associated to it, and the fact that white matter (long-range connections) represents already approximately half of the total mass of the human brain might indicate a tight compromise (Herculano-Houzel et al., 2010). The number of connections, however, is not constant throughout human life. The formation of neuronal connections in the central nervous system is a highly dynamic process, consisting of simultaneous events of elimination and formation of connections (Hua and Smith, 2004). Studies suggest that a common rule in many parts of the brain consists of an initial stage where the creation of connections dominates, peaking during childhood at around 2 years old, and a later reversion stage where pruning dominates until an equilibrium is reached during late adolescence or early adulthood (Huttenlocher, 1979; Lichtman and Colman, 2000; Navlakha et al., 2015). In addition, evidence such as profound changes in dendritic branching in some cortical areas after exposing animals to complex environments and cortical axon remodeling after lesions of the sensory periphery support the idea that structural changes in the wiring diagram might be a vital complement of the learning scheme based on synaptic plasticity (Chklovskii et al., 2004).

Several theoretical variations of the Hopfield network have been proposed to describe the functionality of the hippocampus and other brain areas by means of attractor dynamics, with varying degree of biological plausibility (Amit, 1989; Treves and Rolls, 1991; Kropff and Treves, 2007; Roudi and Latham, 2007). All these variants, however, share a key limitation of the original Hopfield model regarding the number of memories that a network can store and successfully retrieve. Fully connected Hopfield models, for example, can only store a number of patterns equal to a fraction αc ~ 0.138 of the connections per neuron. If more memories are stored, a phase transition occurs and the network loses its ability to retrieve any of the stored patterns. Real brains would need to stay far from the transition point to avoid this risk, a constraint under which networks in the human brain, which has N ~ 1011 neurons but on average only c ~ 104 connections per neuron, would be able to store <p ~ 103 memories, a rather modest number. Error-correcting iterative algorithms as an alternative technique to set the synaptic weight configuration have been shown to increase the storage capacity up to αc = 2 (Forrest, 1988; Gardner, 1988). However, the use of fully connected networks and non-Hebbian modification of synaptic weights limits the applicability of these ideas to model real brains. Random sparse connectivity offers only a relative gain in network performance, allowing the storage capacity to go up to αc = 2/π in ultra-diluted networks, where c ≪ ln(N) (Derrida et al., 1987), or a slightly lower limit in less diluted networks where c ≪ N (Arenzon and Lemke, 1994). Some studies suggest that selective pruning might be much more effective than random dilution in terms of storage capacity, making it diverge for ultra-diluted networks (Montemurro and Tamarit, 2001) or increasing the memory robustness (Janowsky, 1989).

Autoassociative networks gain an order of magnitude in storage capacity when including a more realistic sparse activity (involving ~ 5−10% of neurons per pattern) (Tsodyks and Feigel'man, 1988; Tsodyks, 1989), although this gain is compensated by similar losses related to the incorporation of other biologically plausible elements in either the modeled neurons or the statistics of the stored data (Kropff and Treves, 2007; Roudi and Latham, 2007). Other models that consider the cortex as a network of networks suggest that a hierarchical strategy does not yield considerable benefits, since the number of bits of information that can be stored per synaptic variable is very similar to that of simpler models (Kropff and Treves, 2005).

What other strategies could have been developed by our brains to increase the storage capacity beyond the limit of hundreds of memories predicted by the Hopfield model? In this work we explore the possibility of introducing modifications to the architecture of connections with the aim of improving the signal-to-noise ratio. This process could be analogous to the formation and pruning of connections that reshapes our brains throughout maturation. In the first section we show through numerical simulations that autoassociative networks are able to increase their storage capacity up to around seven-fold by minimizing the noise. In the second section, we show that if the cost function aims to reinforce the signal rather than minimizing the noise, a gain of up to almost one order of magnitude can be obtained. In the last section we implement an algorithm where connections are constantly added and pruned as the network learns new patterns, showing that it converges to the same connectivity with optimal storage capacity regardless of the starting conditions, and that if initial conditions are of low connectivity it reaches an early maximum followed by a long period of decay, as is the case generally in the human cortex.

2. Materials and methods 2.1. Hopfield model 2.1.1. Autoassociative network

For simplicity, we utilized a network similar to the one originally proposed by Hopfield, capable of storing information in the form of activity patterns that can be later retrieved by a partial cue. The network consists of N recurrently connected neurons, each receiving c pre-synaptic connections with no self-connections. The state of neuron i at time t is represented by sit and can take two possible values: sit=1 (“active”) or sit=-1 (“inactive”). The activity of the network evolves synchronously at discrete time steps. At each time step neurons receive a local activity field given by the weighted sum of the activity of other neurons

hit=1c∑j=1NWijCijsjt,    (1)

where Wij represents the synaptic weight between the pre-synaptic neuron j and the post-synaptic neuron i, Cij is a binary matrix taking a value of 1 if this physical connection exists and 0 otherwise and c is the number of pre-synaptic connections targeting a given neuron, so that ∑j=1NCij=c for all i (Cii = 0 because there are no self-connections). Since we are interested in studying the effects of adding and removing connections, it is convenient to consider separately a synaptic matrix W¯¯ with values that only depend on the stored patterns and a matrix C¯¯ that only indicates whether or not the connection exists.

After calculating hit, neurons update their state following a deterministic update rule,

sit+1=sgn(hit),    (2)

where the function sgn(x) returns the sign of x.

Synaptic weights are computed following a linear Hebbian rule,

Wij=∑μ=1pξiμξjμ,    (3)

where ξiμ represents the state of neuron i in pattern μ, from a total amount of p stored patterns. In the classic Hopfield model (and in this work), activity patterns come from the random distribution,

P(ξiμ)=12δ(ξiμ-1)+12δ(ξiμ+1).    (4) 2.1.2. Storage capacity

The relevant parameter that describes the storage capacity of a network is α = p/c. A critical value αc exists where, if more patterns are loaded, the network suffers a phase transition to an amnesic state. This phase transition can be understood in terms of the local activity field each neuron receives. If the network has p patterns ideally stored (i.e., every pattern is exactly a fix point of the network dynamics) and at time t the network is initialized so that the state of each neuron corresponds to a given pattern ξ̄ν (i.e., sit=ξiν for all neurons), then no changes in the neuronal states should occur as a consequence of the update rule in Equation (2), i.e., sit+1=sit=ξiν. To understand this, the local activity field that neuron i receives hit≡hiν can be split into a signal term ξiν (resulting from the contributions of stored information corresponding to pattern ν) and a noise term Riν (which can be thought of as the contribution of other stored patterns)

sit+1=sgn(hiν),      hiν=ξiν+1c∑j=1N∑μ≠νpξiμξjμξjνCij=ξiν+Riν.    (5)

If the local field has the same sign as ξiν, or equivalently, if the aligned local field is positive for each neuron (hiνξiν≡1+Riνξiν>0), then the pattern ξ̄ν will be exactly retrieved. In other words, pattern retrieval depends on whether or not the noise term flips the sign of the aligned local activity field from positive to negative. If connectivity is diluted and random, the aligned local field can be approximated by a random variable following a normal distribution of unitary mean and standard deviation σ~p/c. Since this standard deviation increases monotonically with the number of stored patterns, there is a critical point beyond which the noise fluctuations are large enough to destabilize all patterns and prevent them from being recovered (i.e., hiνξiν<0 for a critical number of neurons).

2.1.3. Basin of attraction

A fundamental characteristic of the attractor states of a Hopfield network is their basin of attraction. It is a quantification of the network's tolerance to errors in the initial state. The basin of attraction depends on the connectivity of the network and the number of patterns stored. In randomly connected networks with low memory load (p ≪ pc), every pattern can be retrieved if the cue provided to the network represents at least 50% of the pattern (<50% is a cue for the retrieval of a stable spurious state represented by flipping all elements in the pattern). As the memory load approaches the critical value pc, tolerance to error smoothly weakens.

We studied memory robustness by simulating networks with different connectivity and memory load. For each initial error, we counted the number of patterns the network could successfully retrieve (e.g., initializing the network in pattern ξ̄ν with an error of 0.2 implied that 20% of the neurons initially deviated from the pattern). We studied the percentage of successfully retrieved patterns as a function of error and memory load.

2.2. Simulations

Simulations were run in custom made scripts written in MATLAB (RRID:SCR_001622). In all sections, the connectivity matrix C¯¯ of each simulated network was initially constructed pseudo-randomly. We selected for each of the N neurons its c pre-synaptic connections using MATLAB's function randperm(N−1, c), randomly obtaining the c indexes among their N−1 possible inputs.

In a typical simulation to study storage capacity, we initialized the network in a given pattern ν, i.e., si0=ξiν, and updated the network following Equation (2) for 100 iterations or until the overlap between the pattern and the network state (i.e., 1N∑j=1Nsjtξjν) remained constant. After this, the pattern was classified as successfully retrieved if the overlap between the final state of the network and the pattern ν was >0.7 (implying that the attractor associated to the pattern was stable but possibly slightly distorted by interference with other patterns). Note that, as is usual when working close to the storage capacity limit, we did not require patterns to be exact fixed points of the network dynamics in order to be considered as successfully stored. Unless otherwise specified, the storage capacity of the network was defined as the maximum number of patterns for which the network could successfully retrieve all of them, normalized by c.

2.3. Connectivity optimization 2.3.1. Noise reduction

As described above, the retrieval of memories can be compromised by random fluctuations in the noise term making the aligned local field negative. We asked whether a non-random connectivity matrix could substantially reduce the local noise contribution each neuron received, resulting in an increase in the storage capacity. In order to find an optimal connectivity matrix, we proposed each neuron to select its c pre-synaptic connections by minimizing an energy function

Ei0=∑ν=1p(∑j=1N∑μ≠νpξiμξjμξiνξjνCij)2∝∑ν=1p(Riν)2.    (6)

Note that in an ideal connectivity configuration that cancels Ei0, neuron i would receive zero noise during the retrieval of any of the stored patterns. In order to use the number of pre-synaptic connections as a control parameter, we used a fixed c, implying that this minimization problem is subject to the constraint ∑j=1NCij=c. Other constraints inherent to the nature of the connectivity matrix is that it is binary (Cij∈) with Cii = 0. Thus, the minimization of Equation (6) belongs to the family of quadratic constrained binary optimization problems. To obtain a computationally efficient approximate solution to this problem we implemented an adaptation of the simulated annealing algorithm. We applied independently to each neuron's pre-synaptic connectivity an annealing schedule where temperature T was decreased by a factor of 0.99 at each step. For each neuron i, we randomly selected two elements in the i-th row of the connectivity matrix C¯¯ and permuted them, which ensured an invariant c. The change was always accepted if the cost function Ei0 decreased (ΔEi0<0), or otherwise with a probability equal to e-ΔEi0/T. Initial temperature was estimated following the method detailed by Yang (2014) and final temperature was set to 10−4.

2.3.2. Signal reinforcement

We proposed a second cost function which can be thought of as a generalization of Equation (6). In this case, the aim is not to minimize the noise but instead to reinforce the signal, contributing positively to the aligned local field by making Riνξiν>0,

Eiϵ=∑ν=1p(∑j=1N∑μ≠νpξiμξjμξiνξjνCij-ϵ)2∝∑ν=1p(Riνξiν-ϵ)2,    (7)

where ϵ is a non-negative parameter. Note that setting ϵ = 0 makes this problem equivalent to the noise reduction scenario.

Results shown in Section 3.2 correspond to optimizations with ϵ = p (we refer to the energy function in Equation 7 as Eip). This arbitrary choice is justified by the observation in a preliminary analysis that the optimization with this value of ϵ nearly maximized the number of patterns where noise contributed positively to the local field for a wide range of values of c, p, and N.

2.3.3. Online algorithm

As mentioned in Section 1, addition and pruning of connections are features of brain maturation. To gain an insight into the role they could play in a learning network, we also proposed an online optimization algorithm where the incorporation of memories and the modification of the connectivity through signal reinforcement occurred in parallel. Our aims were to understand if a similar improvement in storage capacity could be achieved through this on-line approach and to study the dynamics of connectivity.

Algorithm 1 consisted of a heuristic optimization where each neuron would independently attempt to minimize Eiϵ (Equation 7) by eliminating and generating input connections. The main difference with the previous approach is that in order not to disrupt the natural dynamics of the network, annealing was not used (equivalent to setting T = 0 throughout the optimization). In other words, the algorithm was deterministic in the sense that changes in connectivity were only accepted if they diminished the cost function. The resulting greedy optimization scheme, however, often failed to escape local minima. We found that the relaxation of the performance criterion (90% of patterns retrieved instead of 100%) gave enough flexibility for the algorithm to escape these local minima and actually achieve an overall performance similar to the one obtained with simulated annealing. Therefore, we defined the variable peff as the effective number of patterns the network could successfully retrieve, from a total amount of p, where peff > 0.9p.

ALGORITHM 1

Algorithm 1 Online algorithm.

Given N neurons and c0 connections per neuron, we constructed the network's initial random connectivity matrix following the steps detailed before in Section 2.2. Then, an initial number p0 of patterns was loaded, equal to its maximum memory capacity, following Equation (3). Given these initial conditions, we alternated the optimization of the network connectivity and the loading of 10 new patterns. Given neuron i, a pre-synaptic neuron j was randomly selected using randi(N−1) function. If a connection existed for this combination of pre- and post-synaptic neurons (Cij = 1), the effect of eliminating the connection was assessed, and inversely the effect of adding the connection was assessed if Cij = 0. In both cases, the modification of Cij was kept only if it reduced the local energy. This trial-and-error sequence was repeated 10 times for each neuron, after which pattern stability was tested. If more than 90% of patterns were successfully retrieved, a new set of 10 patterns was loaded. Otherwise, the optimization of Cij was repeated until the retrieval condition was met. The algorithm stopped whenever the network's connectivity matrix did not vary for 50 consecutive repetitions. Since the memory load was no longer fixed, we set the parameter ϵ to a constant value throughout the optimization. In Section 3, we fixed ϵ = N/2.

3. Results 3.1. Noise reduction 3.1.1. Storage capacity

We first simulated networks of different size, with a number of neurons N∈ and a number of pre-synaptic connections per neuron covering the full range from highly diluted to fully connected. In each simulation, the connectivity matrix was optimized by implementing the simulated annealing algorithm, which minimized the cost function Ei0 for each neuron (Equation 6). As a result, we obtained an increment in the storage capacity for all values of N and c. We plotted the ratio between the maximum number of patterns stored by optimized vs. random networks in otherwise identical settings, pcopt/pcrand (Figure 1A). This ratio peaked for a connectivity around c/N ~ 0.20, independently of the network size, with a storage capacity for optimized networks up to seven-fold higher than the capacity for random networks. For more diluted networks the factor of improvement over random networks decreased. In the highly diluted extreme, c/N → 0, the improvement ratio tended to 3, while in the opposite limit c/N → 1 it tended to 1, which can be explained by the absence of degrees of freedom left for the optimization to proceed.

FIGURE 1

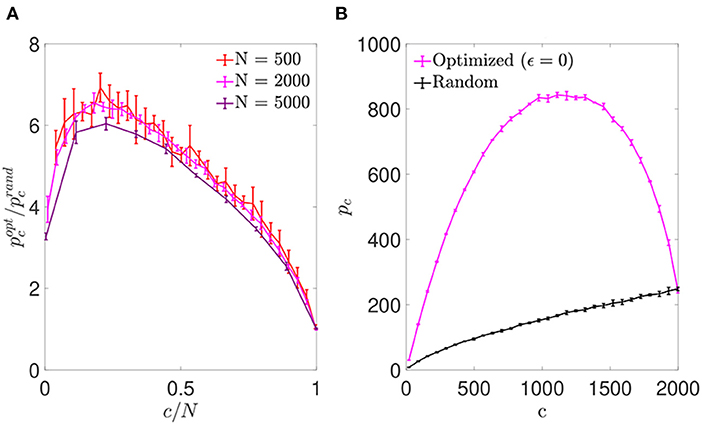
Figure 1. Networks optimized by noise reduction outperform randomly connected ones in terms of storage capacity. (A) Ratio between the storage capacity for optimized (pcopt) and random (pcrand) connectivity as a function of the number of connections per neuron for networks of different N (color coded; mean ± s.d.). (B) Overall maximum number of patterns (not normalized by c) that can be stored and retrieved in an optimized (magenta) or random (black) network of N = 2, 000 as a function of c (mean ± s.d.). Note that the maxima for pcopt/pcrand(A) and pcopt(B) occur for different connectivity levels, implying that more patterns can be stored using a higher number of less efficient connections. Pool of data corresponding to five simulations for each connectivity.

For simulations of increasing c and fixed N, the optimization tended to break the monotonic dependence between pc and c found in random networks (where pc is maximal for fully connected networks; Figure 1B). We found that the maximum number of stored patterns (not normalized by c) peaked at a connectivity near c/N ~ 0.59, different from the connectivity for which the improvement ratio maximized. This could be explained by a compromise allowing to maximize the overall amount of stored information by including a greater number of less efficient connections.

3.1.2. Structural connectivity analysis

We estimated from the resulting connectivity matrices the conditional probability distribution that, given the synaptic weight Wij, neurons i and j were connected in the optimized scheme. In a network with random connectivity, this probability is independent of Wij because by definition P(Cij=1)=cN-1, but this was no longer the case in optimized networks. To improve visual comparison of results obtained for different c and p, we plotted this conditional probability P(Cij = 1|Wij) vs. Wij/WM (Figure 2), which represents the available weights normalized by the maximum absolute value reached by the synaptic weight matrix,

WM=maxi≠j1≤i,j≤N.    (8)

Note that WM is not necessarily equal to p, the maximum theoretical absolute value for Wij. The probability that a given Wij takes a value p is equivalent to the probability of success in p consecutive coin flips, which becomes increasingly unlikely as p grows.

FIGURE 2

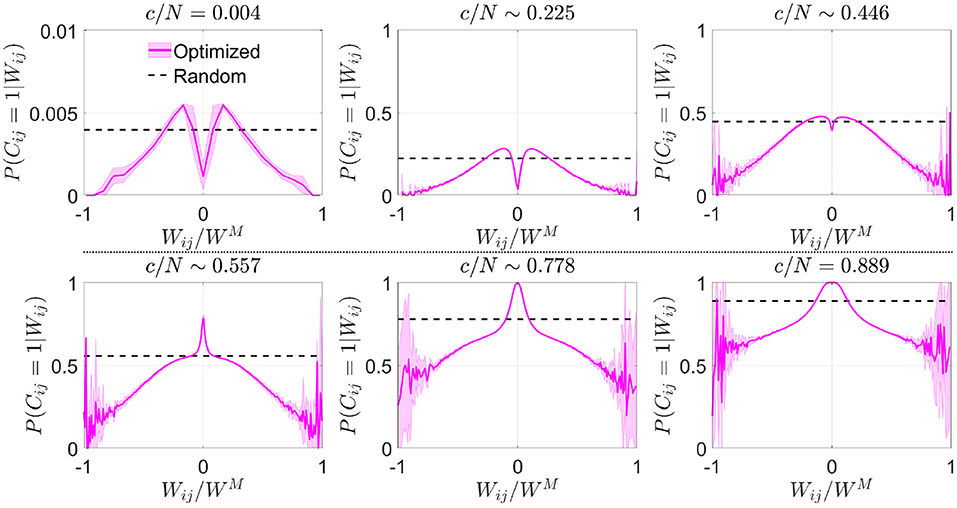
Figure 2. Optimization by noise reduction avoids connections with high absolute synaptic weight. Distribution of the conditional probability of having a connection between two neurons given their associated Hebbian weight for optimized (magenta; mean ± s.d.; N = 5,000) or random (dashed black; theoretical mean) networks. Each panel corresponds to a different connectivity value (indicated). Note that in some cases fluctuations are observed close to |Wij/WM|~1, which are caused by a low number of available data points for extreme values of synaptic weight. Pool of data corresponding to five simulations for each connectivity.

In comparison with the uniform distribution, we observed that the optimized network in the sparse connectivity region tended to favor synapses within a range of low weight values, avoiding those with extreme high or low absolute weight (Figure 2). As connectivity increased, the network started to make use of close-to-zero weights, while still avoiding synapses with high absolute weight. After reaching the connectivity region near c/N ~ 0.59 (where pattern storage peaked), a sudden boost in the use of connections with close-to-zero weight was observed. We speculate that the reason behind this behavior is that optimization at this point minimizes the contribution of new connections to the local field. Eventually, synapses with high absolute weight were included, but always with a probability lower than in random networks.

3.1.3. Signal-to-noise analysis

We next characterized the aligned local field distribution (hiνξiν) in optimized networks. Given that the heuristic minimization of Ei0 never took the cost function to exactly zero, neurons received, on average, a non-zero noise contribution, expected to be lower than in randomly connected networks. We analyzed this distribution for different memory loads in a network with fixed c and N (Figure 3A). In contrast to randomly connected networks, the mean aligned field tended to decrease with α, which implied that the optimization found it convenient to anti-correlate the noise and the signal as a means of minimizing Ei0. In spite of this anti-correlation, retrieval was possible for a larger range of α values than what was observed with otherwise identical random networks.

FIGURE 3

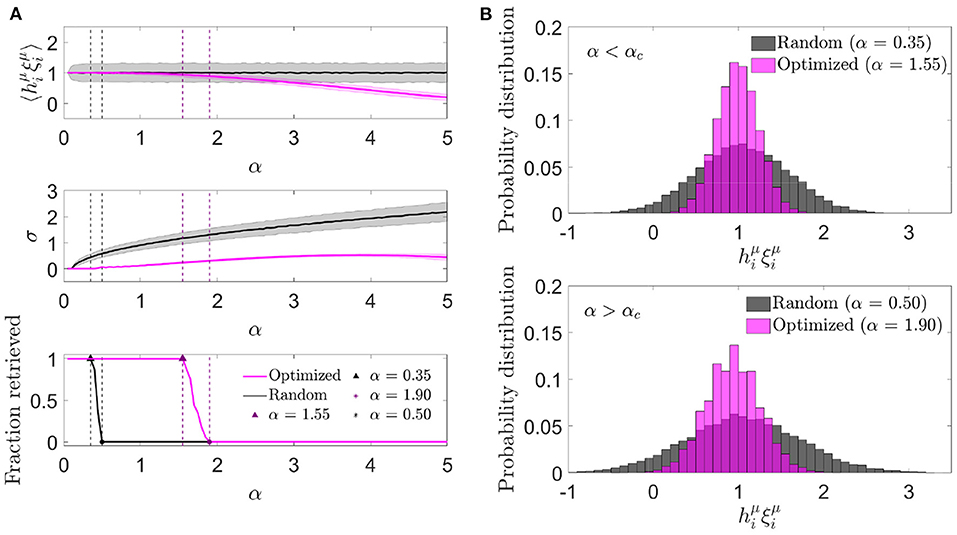
Figure 3. Noise in optimized networks has a reduced variability at the expense of a negative mean. (A) One representative simulation distribution across neurons of the average (top) and standard deviation (center) of the aligned local field (mean ± s.d.), together with the fraction of retrieved patterns (bottom) as a function of the memory load, for optimized (magenta) or random (black) networks. (B) Distribution of the aligned local field for specific memory loads slightly lower (top) and higher (bottom) than the storage capacity [indicated in (A)] for both kinds of network (same color code). All plots correspond to networks with N = 2, 000 and c = 20.

We next studied the standard deviation of the local field to understand if a decrease in variability was compensating for the a priori negative effect of a decrease in mean aligned local field. We observed that, indeed, the increment in the storage capacity could be explained by a substantially narrower noise distribution than the one obtained with random connectivity (Figure 3B). This suggests that fluctuations of the noise term were small enough to let the network store patterns beyond the classical limit, even if they occurred around a negative mean.

The unexpected finding that, in order to minimize the overall noise, the optimization tended to decrease the mean aligned field to values lower than 1 (implying a negative mean aligned noise), led us to ask if better cost functions would lead to a situation in which the noise reinforced the signal, thus improving the overall performance of the network. We explore this possibility in Section 3.2.

3.1.4. Basin of attraction

We next studied the basin of attraction in optimized networks to understand if an increase in storage capacity came at the cost of a reduction in attractor strength (Figure 4). We observed that for most connectivity levels the basin of attraction was only moderately reduced. This reduction was comparable to the one observed in random networks, although the transition to the amnesic phase was smoother. The highest contrast with the behavior of random networks was observed in the case of diluted optimized networks (c/N = 0.01), where large basins of attraction were observed for values of the memory load α up to around 0.7, above which they tended to be very small. Close to the storage capacity limit, although α was high, the attractors were very weak, as a pattern could only be retrieved if the initial state was almost identical to it. However, for c/N = 0.25, a connectivity within the region where the maximum improvement ratio in storage capacity was achieved (Figure 1), attractors were more robust than in diluted optimized networks, and only slightly less robust than in random networks at a comparable distance from the critical storage capacity.

FIGURE 4

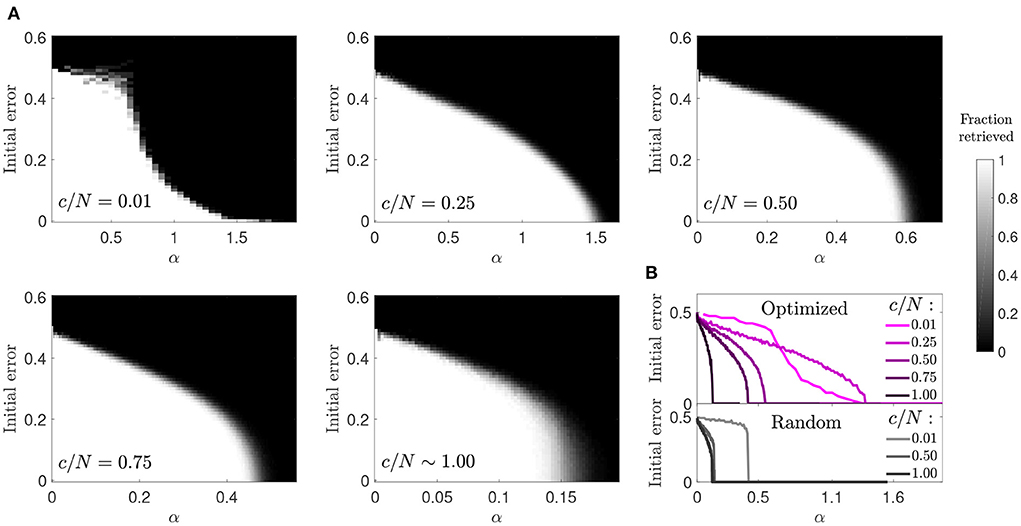
Figure 4. Reduced basin of attraction in optimized networks with diluted connectivity. (A) Fraction of patterns that a network of N = 2, 000 can successfully retrieve (gray-scale), relative to the initial error. (B) Phase transition curves from (A) condensed in a single plot (top) together with similar curves corresponding to a random network (bottom). Connectivity is color coded.

The increase in the size of the basin of attraction from c/N = 0.01 to c/N = 0.25 in optimized networks is counter intuitive, but analytic modeling of networks with random connectivity provides a potential explanation (Roudi and Treves, 2004). In a non-diluted, random connectivity network, the field of a given neuron has a noise term proportional to its activity, caused by feedback of the neuron's activity state through multiple-synaptic loops. The probability of existence of such connectivity loops, starting in the neuron and projecting back to it, decreases toward zero in diluted networks, and so thus the effect of this noise term. It is possible that the optimized network leverages from multi-synaptic feedback loops to increase the robustness of attractors, as the sudden decay in the size of the basin of attraction but not in overall storage capacity from c/N = 0.25 to c/N = 0.01 seems to suggest.

3.2. Signal reinforcement 3.2.1. Storage capacity

Inspired by the results in the previous section, we next assessed the possibility of optimization by reinforcement of the signal rather than noise reduction, by using the same optimization procedure with a different cost function (Equation 7). We observed that, as in the previous section, the optimization process increased the storage capacity of autoassociative networks (Figure 5A). However, in contrast to the ϵ = 0 case, the improvement ratio pcopt/pcrand for the optimization with ϵ = p increased monotonically with network dilution for most of the c/N range, reaching its best performance pcopt/pcrand~10 around the lowest connectivity values.

FIGURE 5

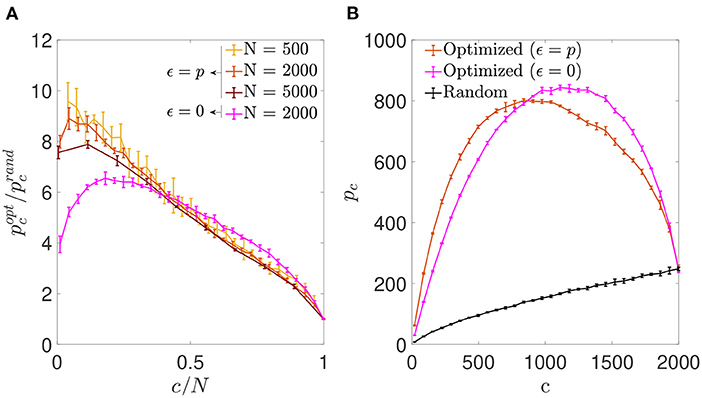
Figure 5. Signal reinforcement outperforms noise reduction and is optimal with highly diluted connectivity. (A) Ratio between the storage capacity for optimized (pcopt) and random (pcrand) connectivity as a function of the number of connections per neuron for networks of different N (shades of red; mean ± s.d.). For comparison, the curve corresponding to noise reduction is included (magenta; N = 2, 000). (B) Overall maximum number of patterns (not normalized by c) that can be stored and retrieved as a function of c in a network with N = 2, 000 optimized by signal reinforcement (orange), optimized by noise reduction (magenta) or with random connectivity (black) (mean ± s.d.). Note that, as in Figure 1, the maxima for pcopt/pcrand(A) and pcopt(B) occur for different connectivity levels. Pool of data corresponding to five simulations for each connectivity.

We also observed that the overall number of patterns p that a network of fixed N could store and retrieve was higher if optimized by minimizing Eip than by minimizing Ei0 in the low connectivity range (Figure 5B), but the opposite was true for high connectivity. While the connectivity capable of storing more patterns for the optimization with ϵ = 0 was near c/N ~ 0.59, for the optimization ϵ = p it was c/N ~ 0.42, with slightly fewer patterns in total. However, both of these limits are far from the biologically plausible limit of high dilution, where signal-reinforcing networks seem to outperform noise-minimization ones.

We next plotted the αc curves as a function of c/N (Figure 6), which allowed for a better visualization of the fact that for a connectivity of c/N = 0.01, both optimizations achieved an enhanced storage capacity, in the case of signal-reinforcement networks up to an order of magnitude greater than obtained using random connectivity. When minimizing Ei0, the capacity was close to αc ~ 1.49, while in Eip minimization, the critical capacity more than doubled the latter, reaching αc ~ 3.15.

FIGURE 6