1 Introduction

Walking serves as the foundation for humanoid robots to operate stably in various environments, its dynamics and robustness directly affect the robot's work efficiency. With the significant advancement of humanoid robot structures and actuators, many researchers have conducted in-depth studies on leg control and stable walking control methods. Although numerous impressive results have been achieved, these methods still struggle to support high-speed walking for humanoid robots in emergency scenarios (Xiaobin and Aaron, 2022; Yu-Ming et al., 2024). Therefore, further enhancing the dynamic performance and disturbance rejection capability of humanoid walking has become a key objective in humanoid robot research. According to bionic studies, humans primarily counteract self-induced or external disturbances during walking by adjusting footstep placement and coordinating whole-body limb movements (Horak and Nashner, 1986; Thierry et al., 2001). Inspired by humans, enhancing the dynamic walking capability of humanoid robots requires motion control systems that not only incorporate highly effective footstep planning to regulate the CoM velocity but also enable coordinated control of all joints to maintain stability. Consequently, the development of efficient footstep planning methods and the incorporation of whole-body coordination strategies involving the waist and arms have become key priorities for future humanoid robot research.

The Linear Inverted Pendulum (LIP) and the Spring-Loaded Inverted Pendulum (SLIP) are the most effective simplified models derived from the characteristics of CoM motion in biological movements (George et al., 2023; Xiaolong et al., 2024). The SLIP model, due to its dynamic properties, is commonly applied in the dynamic motion control of quadruped robots, including diagonal trotting, jumping, and galloping gaits (Dominic et al., 2018; Sovukluk et al., 2024). However, its dynamic characteristics pose challenges for humanoid robots with distributed mass, particularly in state estimation and joint impedance control, making it difficult to apply in real-world systems (Hong et al., 2022; Stéphane et al., 2020). The LIP model is widely utilized in the walking planning and control of humanoid robots across complex terrains, such as flat surfaces, slopes, and stairs. A pioneering study combined MPC with the Zero Moment Point (ZMP) approach, using the cart-table model to plan the robot's CoM trajectory, and designed an online controller to track the desired ZMP for stable walking of the humanoid robot (Kajita et al., 2003). However, these methods require high-precision foot sensors to accurately sense contact forces, which are impractical for real-world environments with complex terrains. Additionally, the ZMP stability criterion is not applicable to humanoid robot systems equipped with point or line-shaped feet, which limits its applicability. The MPC algorithm, due to its feedback correction and rolling optimization features, has been widely applied in footstep trajectory generation tasks. Nicola et al. (2020) proposed the Inherently Stable Model Predictive Control (IS-MPC) framework, which uses the LIP dynamics model as the prediction model and ZMP velocity as the control input. This method generates a gait, including time frames, in real-time to achieve omnidirectional motion commands. Elham et al. (2021) implemented stable walking for the small bipedal robot Blot using a hierarchical MPC framework. Guiyang et al. (2021) combined MPC and the LIP dynamics model to create an efficiently computed footstep prediction planner for quick response to disturbances during walking. The MPC controller has become a powerful tool for humanoid robot walking control (Patrick et al., 2023). However, in current applications, there are often issues with large CoM velocity tracking errors and limited iterations, making it difficult to meet the accuracy requirements for tracking desired average speed during humanoid robot walking.

After the robot obtains the optimal footstep positions, the desired CoM trajectory and swing leg trajectory can be obtained through integration of the LIP dynamics equations and polynomial fitting. The primary task of the motion control system is to input optimal joint drive commands to effectively track the specified task trajectory. When a humanoid robot is performing high-speed dynamic walking, the control system faces two main challenges. The first challenge is that, during walking, the robot's step length increases with the desired speed. If the step length is too long, it may cause the robot to reach mechanical limits or result in a smaller adjustable range for foot placement. The swing leg may fail to reach the desired footstep position, preventing the robot from effectively controlling the CoM motion, which could lead to a fall. To address this issue, related biological studies have found through human gait motion capture data that the waist rotates with the swinging of the legs during walking, and its range of rotation increases with the step length. Some robotic researchers have innovatively incorporated this characteristic into motion control systems. Beomyeong et al. (2020) analyzed the impact of the waist on the kinematics of humanoid robots and concluded that the introduction of the waist can enhance the range of motion of the robot's legs. Based on this conclusion, they designed an optimization problem to generate the waist motion trajectory, thereby improving the walking capability of the robot Dyros-Jet. Jehwi et al. (2021) compared the energy consumption and joint torque between fixed waist and coordinated waist motion walking strategies. The results indicated that the coordinated waist walking method could reduce the robot's energy consumption during movement, particularly alleviating the load torque on the knee joints. Hyobin and Inho (2022) introduced the waist into the kinematics of humanoid robot standing tasks, significantly enhancing its flexibility and operational range. Based on the findings from the above studies, it is evident that the effective control of waist motion can improve the range of motion of the robot's legs while reducing energy consumption during walking. The second challenge arises from the fact that as the robot's walking speed increases, the legs need to perform high-frequency, large-amplitude swings to track the desired footstep positions. The reaction forces and torques generated during the swinging motion can cause significant disturbances to the robot's body posture, affecting the stability of the walking process. To address this challenge, some studies have proposed using the waist to drive body rotation in order to compensate for the momentum during walking. However, using torso rotation to balance the disturbance angular momentum leads to large-scale body rotations, which increases the non-linearity of the robot's dynamics. This not only complicates the control but also affects the role the waist must play during the swing leg phase. Since the arms have no external contact forces or specified trajectory tasks during walking, they can swing freely over a wide range. Therefore, using the arms to counteract disturbance momentum is an effective solution. Zhifa et al. (2023) planned the arm swing trajectory, using the arm swing to counteract the disturbances caused by the swinging leg, thereby improving the stability of the bipedal robot during dynamic walking. Dragomir and Ryo (2022) focused on the issue of robotic angular momentum and inherent redundant degrees of freedom, using the angular momentum generated by the swinging arms to counteract external disturbances, thereby enhancing the robot's ability to resist external perturbations. Beomyeong et al. (2020) used the swinging of arms to compensate for the robot's yaw angular momentum during walking, achieving stable walking for the robot. Georg et al. (2016) treated the arms of the Atlas robot as a flywheel system to control the robot's Centroidal Moment Pivot (CMP) and enable real-time tracking of the Instantaneous Capture Point (ICP), achieving walking on a balance beam, a task with extremely high stability requirements. Based on the above research, it is clear that the advantage of using arm swing to counteract disturbances lies in the fact that, during normal walking, the robot's arms do not need to engage in force interaction tasks with the external environment. Moreover, the arm movements are decoupled from the leg movements, allowing for flexible arm swings based on the needs. Unfortunately, the aforementioned studies mainly focus on scenarios such as slow walking or standing in humanoid robots, and do not delve into the arm swing control methods in the context of dynamic walking.

Based on the above analysis, this paper aims to enhance the walking capability of humanoid robots by integrating relevant research and conclusions from human gait studies. A walking control framework consisting of the improved footstep planner and the whole-body coordination controller is designed, as shown in Figure 1. In this framework, the improved footstep planner constructs the MPC optimization problem using the position component of the solution to the differential equation in the LIP model. By leveraging the advantages of MPC's rolling optimization, the optimal footstep position can be quickly determined based on the robot's desired walking speed and current motion state. The motion trajectory planner in the walking task space is capable of planning the robot's CoM trajectory, swing leg trajectory, and other whole-body movements based on the desired footstep positions, and then sending these plans to the motion controller for execution. The whole-body coordination controller, based on the given task requirements, controls the robot to achieve stable walking. Compared to existing studies, the walking control framework proposed in this paper deeply draws from human walking strategies, fully utilizing all the degrees of freedom of the humanoid robot, significantly enhancing its dynamic walking capability. The main contributions of this paper are as follows:

1) This paper proposes an improved footstep planner, which is based on an enhancement of the traditional LIP-MPC approach. First, the desired CoM displacement is described using the desired speed and footstep time. Then, the LIP position differential equation solution is used to replace the traditional instantaneous velocity differential for predicting the CoM state. Finally, a quadratic optimization problem is formulated to solve for the robot's optimal footstep position. The improved planner avoids the average speed tracking errors caused by the instantaneous velocity iteration optimization in traditional methods, thereby enhancing the robot's control accuracy over the average walking speed.

2) For dynamic walking of the robot, a coordination strategy for the robot's arms and waist is planned, based on the characteristics of human walking. The whole-body coordination controller is then designed according to the established strategy. The controller adopts a hierarchical WBC design approach, consisting of two components: the Lower-body WBC and the Upper-body WBC. The Lower-body WBC coordinates the robot's legs and waist, fully utilizing the structural advantages of the robot to achieve large-step walking. The Upper-body WBC controller manages the robot's arms to compensate for the centroidal angular momentum. This controller addresses the issue of poor task control performance caused by the coupling of multiple control tasks in humanoid robots with redundant degrees of freedom, significantly enhancing the robot's dynamic walking capability.

3) The improved footstep planner and the whole-body coordination controller are integrated into a humanoid robot walking control framework, and the proposed framework is validated through simulation experiments. The simulation results show that the walking control framework proposed in this paper significantly enhances the robot's dynamic walking ability, demonstrating its feasibility and effectiveness.

Figure 1. Humanoid robot walking control framework.

The rest of this paper is organized as follows: In Section 2, the derivation of the LIP dynamics model is presented, and the design method for the improved footstep planner is proposed. Section 3 describes the walking control strategy proposed in this paper, and based on this, the design of the whole-body coordination controller is presented. In Section 4, we integrate the improved footstep planner and the whole-body coordination controller, and perform simulation validation. The results demonstrate the advantages of the proposed control framework. Finally, in Section 5, the paper is summarized, and future work is discussed.

2 Improved footstep planner 2.1 Motion analysis of the LIP model

The LIP model has been widely applied to humanoid robot walking control and has demonstrated excellent control performance. By treating the CoM of a humanoid robot as the CoM of the LIP model, the complex motion of a humanoid robot can be simplified to the simple LIP model (Lim et al., 2012, 2004). Assume that after each footstep, the center of the supporting foot is taken as the current origin of the coordinate system. The intersection of the sagittal with the ground forms the x-axis of the coordinate system, and the intersection of the coronal with the ground forms the y-axis. In the motion process, it is assumed that the CoM of the LIP model has no deviation in the z-axis direction from the desired height and is subjected to a constant thrust of mg. Taking the x-axis as an example, in the coordinate system of the contact foot, the dynamics equations can be expressed as:

ẍcom=gzcom-pz(xcom-px)    (1)

Where g is the gravitational acceleration, zcom is the constant height of the robot's CoM, and px represents the x-axis footstep coordinates in the current coordinate system. The LIP dynamics model can be treated as a differential equation, and its solution can be obtained as:

x(t)=A(t)X0+B(t)px    (2)

Where X=[xcomẋcom]T represents the CoM state vector, and X0 denotes the initial state of the CoM. The coefficients A(t) and B(t) are defined as:

A(t)=[cosh(ωt)ω-1sinh(ωt)ωsinh(ωt)cosh(ωt)]    (3) B(t)=[1-cosh(ωt)-ωsinh(ωt)]    (4)

From the above equations, the future CoM motion state of the robot satisfying the LIP dynamics model at a specific time can be quickly calculated based on the current CoM state X0, without requiring complex iterative calculations of the dynamic equations.

Based on the solution of the above LIP dynamics differential equations, the robot's motion state at future time can be quickly computed. The illustration of the LIP single-cycle motion is shown in Figure 2. Given the current contact point coordinates as px0, which is set as the origin of the world coordinate system for the current walking cycle. At the current time t0, the current CoM position and velocity are xcom0 and ẋcom0, respectively. The position and velocity of the CoM at the end of the support phase at time te0 can be expressed as xcom0,e and ẋcom0,e, respectively. The equations can be written as:

X(te0)=[xcom0,eẋcom0,e]=A(te0-t0)[xcom0ẋcom0]+B(te0-t0)px0    (6)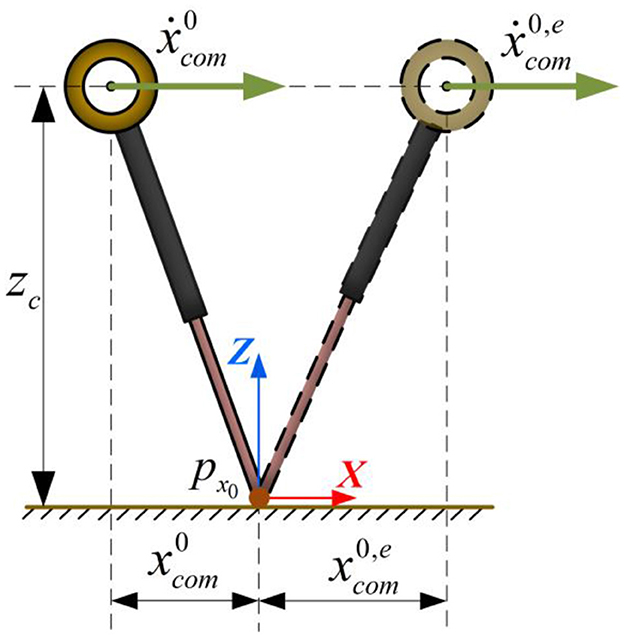

Figure 2. The LIP single-cycle motion process.

When a humanoid robot performs dynamic walking, the double-support phase is typically neglected. The left and right feet alternately execute a single-support phase according to the set motion cycle, generating reaction forces to maintain the robot's walking. Assuming no significant collision or energy loss during the support foot transition, the CoM motion state at the end of the current support phase and the beginning of the next support phase can be considered equal, which can be expressed as:

Where n denotes the future n-th step, the superscript “–” indicates the end time of the current support phase, and the superscript “+” indicates the start time of the next support phase. Equation 7 can be further expressed as:

[xcom1+ẋcom1+]=X1+=X0-=A(te0-t0)X0+B(te0-t0)px0    (8)

This allows us to obtain the CoM state at the end of the current support phase and at the beginning of the next step's support phase. Expanding the above equation, the motion state of the robot at the n-th future step in the current coordinate system can be expressed as:

             X2+=X1−=A(Ts1)X1++B(Ts1)px1*             X3+=X2−=A(Ts2)X2++B(Ts2)px2*                                                   ⋮Xn+=Xn−=A(Tsn−1)Xn−1++B(Tsn−1)pxn−1*    (9)

where Tsn is the duration of the n-th future support phase, also referred to as the footstep time.

2.2 MPC framework for footstep adjustment control

In existing research, the traditional LIP-MPC method typically constructs an optimization problem by using the velocity of the CoM state at the end time of each supporting phase as the prediction variable, thereby determining the optimal foot placement. However, based on the analysis of the LIP-based walking process, the CoM velocity exhibits a deceleration followed by acceleration, with varying velocities at different moments during the motion. If the velocity at a certain moment during the walking process is used as the prediction variable, it is difficult to represent the tracking performance of the reference average velocity throughout the entire process. This issue is particularly pronounced when the step frequency is low, as the LIP model experiences significant velocity fluctuations during the motion, resulting in more noticeable tracking errors.

To avoid the impact of instantaneous velocity on the tracking performance, we abandon the traditional optimization method that uses the CoM velocity at the end of the support phase for tracking. Instead, we utilize the CoM position at the end of the support phase as the desired outcome for the optimization problem to improve the robot's foot placement. The advantage of this strategy lies in the fact that, firstly, it maps the LIP motion velocity to the CoM position and footstep time, enabling more accurate tracking of the desired velocity. Additionally, the CoM position provides a more accurate and reliable state estimation compared to the velocity. The predicted trajectory of the CoM motion and the foot placement are illustrated in Figure 3. Based on this illustration, we will describe the details from both the x-z and the y-z.

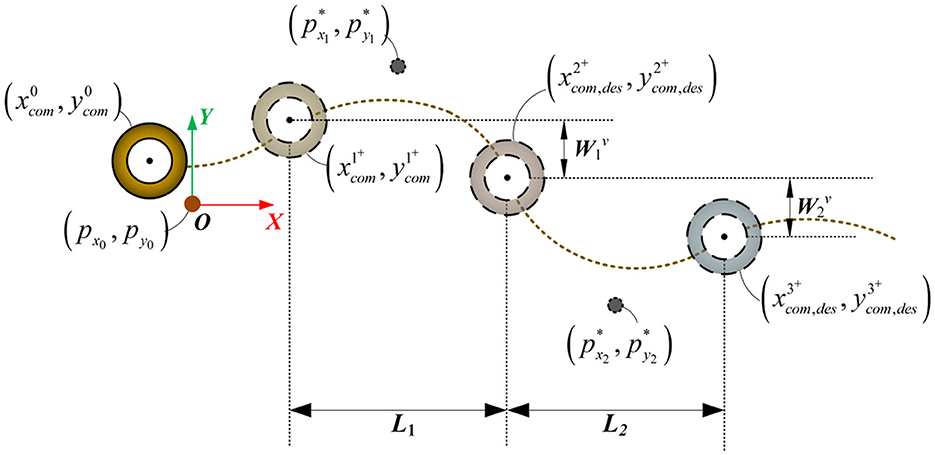
Figure 3. The footstep placement and CoM trajectory in the prediction process of the LIP model.

2.2.1 x-z plane

In the x-z plane, the LIP model tracks the robot's desired walking speed along the x-axis using the foot placement. When the robot's desired walking speed is set to ẋdes, and the single-leg support phase for the future n-th step is Tsn, the step length for the future n-th step can be estimated as:

The x-axis position of the CoM at the end of the support phase during the n-th step can be expressed as:

xcom,desn-=xcom,des(n+1)+=xcom,desn++Ln    (11)

It is assumed that after the robot places its foot, there is no relative displacement between the foot and the ground, and no adjustment can be made. Therefore, during the current support phase, the desired CoM state at the end of the phase is the same as the actual CoM state.

[xcom0-ẋcom0-]=X0-=A(te0-t0)X0+B(te0-t0)px0    (12) xcom,des1+=xcom0-    (13)

Thus, based on the desired velocity, the expected position at the end of each support phase can be iteratively calculated. The illustration of the expected position along the x-axis is shown in Figure 4A.

xcom,des2+=xcom,des1-=xcom,des1++ẋdesTs1xcom,des3+=xcom,des2-=xcom,des2++ẋdesTs2⋮xcom,desn+=xcom,des(n-1)-=xcom,des(n-1)++ẋdesTsn-1    (14)

Therefore, the cost function for the optimization problem in the x-z plane can be constructed as:

minPx*∑i=1n(‖xcom,desi+−xcomi+‖Q