1 Introduction

Emotion recognition is an essential component of daily life, playing an increasingly pivotal role in both interpersonal communication and cognitive decision-making. Consequently, developing more intelligent emotion recognition algorithms is crucial for enhancing both accuracy and efficiency (Chen et al., 2021). Emotion recognition data can be broadly categorized into two types: non-physiological signals [e.g., facial expressions (Huang et al., 2019), speech (Wang et al., 2022)] and physiological signals [e.g., electrocardiograms (ECG) (Meneses Alarcão and Fonseca, 2017), electrodermal activity (EDA) (Veeranki et al., 2024a), and electroencephalograms (EEG) (Veeranki et al., 2024b)]. Although non-physiological signals provide intuitive insights into emotional states, they are subject to manipulation, as individuals may intentionally conceal their true emotions. In contrast, physiological signals offer a more objective reflection of an individual's authentic emotional state (Li et al., 2020). Among these, EEG signals are particularly noteworthy for their ability to capture emotional stimuli directly affecting the central nervous system (Berboth and Morawetz, 2021). As a result, EEG-based emotion recognition is anticipated to attract increasing research attention.

The inherent instability of EEG signals and the complexity of brain structure make it particularly challenging to analyze and extract latent features for distinguishing between emotional states. Current feature learning methods can be broadly classified into traditional machine learning and deep learning approaches. Traditional machine learning methods require manual extraction of shallow features, such as Hjorth parameters, higher-order crossings (HOC), power spectral density (PSD), and differential entropy (DE) (Yan et al., 2022; Jenke et al., 2014; Duan et al., 2013). However, these methods heavily depend on expert knowledge, which may limit a holistic understanding of the intricate emotion-related EEG features. To address these limitations, a growing body of research has turned to deep learning techniques for feature extraction, which has significantly enhanced the performance of emotion recognition systems (Ngai et al., 2021; Zuo et al., 2024b). Currently, deep learning approaches mainly focus on extracting features from the temporal and spatial dimensions. For temporal feature extraction, recurrent neural networks (RNNs) have been employed to capture the dynamic temporal patterns in EEG signals (Wei et al., 2020; Wu et al., 2024; Hu et al., 2024b). Chen et al. (2019) introduced a hierarchical bidirectional gated recurrent unit (BiGRU) network to mitigate the effects of long-term non-stationarity in EEG signals by focusing on temporal features. Similarly, Algarni et al. (2022) utilized a stacked bidirectional long short-term memory (Bi-LSTM) network to generate emotion-related feature sequences in chronological order, achieving an accuracy of 96.87% on the DEAP dataset. While these studies effectively highlight the importance of temporal information, they overlook the topological structure of the brain, which plays a crucial role in understanding brain connectivity in emotional recognition. In terms of spatial feature extraction, convolutional neural networks (CNNs) had become the preferred choice for this domain (Rahman et al., 2021; Bagherzadeh et al., 2022). CNNs possess robust feature extraction capabilities and are adept at effectively processing continuous dense feature maps, thereby demonstrating exceptional performance in handling spatial relationships. However, the sparse spatial structure of EEG channels limits CNNs' ability to fully explore the spatial relationships between channels. To overcome this limitation, graph convolutional networks (GCNs) have been increasingly adopted to model the adjacency relationships between EEG channels. By constructing topological representations of the brain to extract deep spatial features, GCNs have shown significant promise in emotion recognition tasks (Chang et al., 2023; Zong et al., 2024). For instance, Wang et al. (2019) proposed a phase-locking value (PLV)-based graph convolutional neural network (P-GCNN), which constructs an adjacency matrix by calculating the phase synchronization between EEG channels using PLV. This method addresses the discrepancy between the spatial, physical locations of EEG channels and their functional connections. Nevertheless, while static graph construction based on functional connectivity helps to capture stable spatial patterns in EEG signals, its reliance on prior knowledge makes it difficult to dynamically capture the evolving dependencies between nodes driven by emotional fluctuations. Thus, developing a model that effectively integrates both the temporal and spatial features of EEG signals is essential for achieving a more comprehensive and nuanced analysis of emotion recognition.

Effectively capturing the consistency and complementarity of multi-feature information in emotional semantics is a critical area of research in emotion recognition. Consistency refers to the shared semantic information across different features, while complementarity highlights the distinct semantic information unique to each feature. Multi-feature fusion methods are generally divided into three categories: feature-level fusion (Zhang et al., 2024), decision-level fusion (Pu et al., 2023), and model-level fusion (Islam et al., 2024). Feature-level fusion involves combining various features into a single feature vector to form a comprehensive representation. For example, Tao et al. (2024) proposed an attention-based dual-scale fusion convolutional neural network (ADFCNN) that integrates spectral and spatial information from multi-scale EEG data using a concatenation fusion strategy. However, ADFCNN directly merges features from different sources, potentially overlooking essential spatial information within individual features and the temporal synchronization between them. Decision-level fusion, on the other hand, combines multiple predictions using algebraic rules. Dar et al. (2020) utilized CNNs and long short-term memory networks (LSTMs) to separately process EEG signals, followed by a majority voting mechanism to generate the final classification. However, since data is processed independently by different networks, this method limits the transfer of complementary information between features. Model-level fusion aims to foster interactions between different feature domains, allowing the model to uncover correlations and fully exploit the complementary nature of multiple features. Huang et al. (2023) introduced a model called CNN-DSC-BiLSTM-Attention (CDBA), which employs a multi-branch architecture to extract diverse features from EEG signals and uses a self-attention mechanism to assign feature weights for emotion classification. While the self-attention mechanism effectively captures internal dependencies within sequences, it has limitations when it comes to integrating features from various information sources. This shortcoming arises because self-attention primarily focuses on the relevance of local or internal features, often neglecting the complex interactions between multiple feature domains (Hu et al., 2024a). Thus, a comprehensive understanding of the intrinsic connections between emotional expression and spatiotemporal information, along with a precise modeling of the interactions between different features, is crucial for improving the model's capacity to recognize and track emotional patterns effectively.

Given the challenges outlined above, this paper introduces a novel network named the Spatiotemporal Adaptive Fusion Network (STAFNet), which integrates adaptive graph convolution and temporal transformers to enhance the accuracy and robustness of EEG-based emotion recognition. STAFNet is designed to fully exploit both the spatial topological structure and temporal dynamics of EEG signals. The Temporal Self-Transformer Representation Module (TSRM) emphasizes the most informative EEG segments within each channel, enabling the extraction of global contextual temporal information. Simultaneously, the Adaptive Graph Convolutional Module (AGCM) leverages an adaptive adjacency matrix to capture the dynamic patterns of brain activity, thus enabling the extraction of highly discriminative spatial features. Finally, the Multi-Structured Transformer Fusion Module (MSTFM) learns and integrates potential correlations between temporal and spatial features, adaptively merging key features to further boost model performance. The effectiveness of the proposed STAFNet is demonstrated through performance comparisons with state-of-the-art (SOTA) methods and validated via ablation studies. The key innovations of this paper are as follows:

• We propose an AGCM to explore the spatial connections between brain channels. To capture the dynamic changes in brain network structure over time, this module adaptively updates the adjacency matrix during backpropagation, allowing it to reflect temporal variations in brain connectivity.

• We integrated an enhanced transformer into the MSTFM, which employs a novel attention mechanism to effectively fuse complementary spatiotemporal information from EEG signals. This allows the model to capture the intrinsic connections between emotional expression and spatiotemporal features, leading to a significant improvement in classification performance.

• STAFNet employs a dual-branch architecture to seamlessly integrate both temporal and spatial feature information from EEG signals. Experimental results demonstrate that STAFNet outperforms SOTA methods on the public SEED and SEED-IV datasets, showcasing its superior performance in EEG-based emotion recognition.

2 Materials and methods 2.1 Datasets

To evaluate the proposed model, we conducted EEG-based emotion recognition experiments using the Shanghai Jiao Tong University Emotion EEG Database (SEED) (Zheng and Lu, 2015) and its enhanced version, SEED-IV (Zheng et al., 2019). These datasets were employed to demonstrate the effectiveness and robustness of the STAFNet model.

The SEED dataset consists of EEG recordings from 15 participants (7 males and 8 females) while they watched 15 movie clips, each representing one of three emotions: positive, neutral, or negative. Each clip lasted approximately 4 minutes. The experiment was conducted in three separate sessions, with intervals between sessions, resulting in EEG data collected from all 15 participants across three sessions. EEG data were recorded using a 62-channel ESI NeuroScan system, with electrode placement following the international 10-20 system, as illustrated in Figure 1. In total, the SEED dataset contains 675 EEG samples (45 trials per participant for 15 subjects). For each participant, there are 15 samples corresponding to each emotional category.

Figure 1. A schematic diagram of the 62 electrodes in the EEG cap used for the SEED and SEED-IV datasets. The diagram shows the approximate locations of each electrode on the brain.

The experimental process for the SEED-IV dataset is similar to that of the SEED dataset, but with a broader range of emotions and more movie clips. In SEED-IV, 72 movie clips were selected to elicit four emotions: happiness, sadness, fear, and neutrality, offering a wider emotional spectrum compared to SEED. Fifteen participants took part in the experiments, conducted at regular intervals, with each session consisting of 24 trials. EEG data were recorded for each participant using a 62-channel ESI NeuroScan system, following the international 10-20 electrode placement system. The SEED-IV dataset contains a total of 1,080 samples (72 trials per participant across 15 subjects), with each participant contributing 18 samples for each emotion type.

2.2 Preprocessing

In both the SEED and SEED-IV datasets, EEG signals were originally sampled at 1,000 Hz and then downsampled to 200 Hz. To ensure a fair comparison with existing studies (Zeng et al., 2022), we adopted the same preprocessing strategy. First, the EEG data from both datasets were segmented using non-overlapping sliding windows of 1-s duration to maintain temporal continuity and consistency. A 3rd-order Butterworth bandpass filter was then applied to the raw EEG data to retain the frequency bands relevant for emotion recognition while effectively suppressing high-frequency and low-frequency noise. Finally, Z-score normalization was applied to mitigate variability and address non-stationarity in the EEG signals.

2.3 Proposed methodology

Our proposed STAFNet model proficiently extracts and integrates spatial and temporal features from EEG signals, enabling accurate emotion recognition. STAFNet consists of four main functional components: AGCM, TSRM, MSTFM, and CM. The input to the model is represented as X=[x1,…,xn]∈ℝN×T×C, where n denotes the n-th preprocessed EEG sample, N denotes the total number of samples, T denotes the sample length, and C denotes the number of EEG channels. In the entire framework, the preprocessed EEG signals are fed into the STAFNet model, with dimensions denoted as [N, T, C]. Figure 2 provides an overview of the STAFNet model's process for handling EEG data. First, the raw EEG signals are preprocessed and segmented to obtain the input representation X. Next, X are processed through the AGCM and TSRM to extract highly discriminative spatial and temporal features, respectively. Subsequently, the MSTFM is used to integrate the complementary information between spatial and temporal features, resulting in the fused features. Finally, the fused features are processed through the CM layer to obtain the final prediction results.

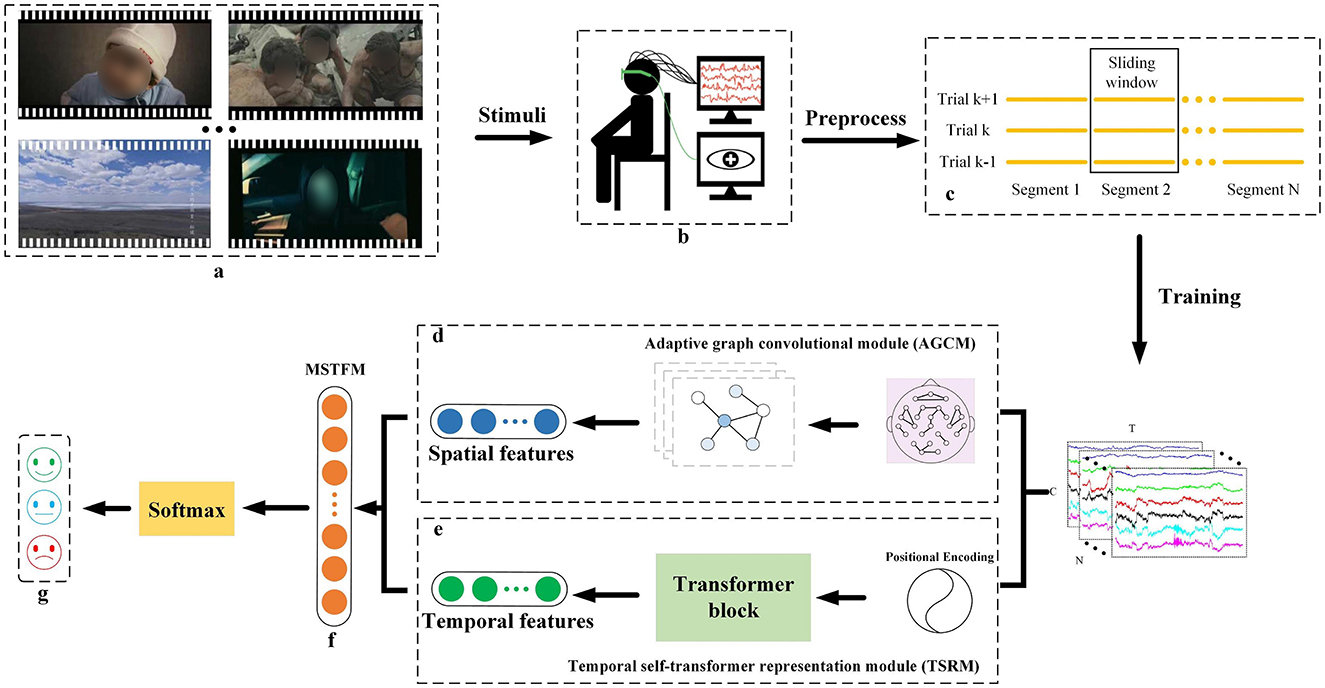
Figure 2. Overview of the STAFNet model architecture for EEG-based emotion recognition. (A) Emotional stimulus; (B) Acquisition of input data; (C) EEG signal slicing; (D) AGCM, which extracts the spatial features of the EEG signals; (E) TSRM, which extracts the temporal features of the EEG signals; (F) MSTFM, which fusion the spatial and temporal features; (G) the classification results.

2.3.1 Adaptive graph convolutional module

The dynamic connectivity patterns underlying emotional changes rely heavily on the spatial connections between electrodes. Thus, accurate connectivity estimation is crucial for understanding the interactions and information flow between different brain regions (Zuo et al., 2024a, 2023). We introduces an AGCM based on an adaptive adjacency matrix to capture spatial variation information. Specifically, we use a directed weighted graph G = (V, A), where V = denotes the set of vertices with n nodes, and the adjacency matrix A = (ai,j)n×n describes the edge weights between nodes in V. Each element ai,j denotes the coupling strength of the connection between node i and node j.

To evaluate the potential relational variations between any two electrode channels, we propose a novel method for adaptively and dynamically learning the relationships between adjacent nodes, as illustrated in Figure 3. First, an adjacency matrix AD∈ℝC×C is randomly initialized, where C denotes the number of channels. This adjacency matrix reflects the correlations between each pair of channels, accounting for both direction and intensity. Then, during model training, the weights of all channels in the adjacency matrix AD are dynamically updated through a backpropagation mechanism, with the calculation formula as follows:

{Ã=W2δ(W1A)ÃD=σ(Ã)    (1)

where W1∈ℝ(C×Cr)×(C×C) and W2∈ℝ(C×C)×(C×Cr) denote the weight matrices, δ(·) and σ(·) denote the Tanh and Relu function, and r is the reduction ratio. We introduce the Tanh function to model the directionality between different channels and employ an activation function Relu to enhance the coupling of significant channels while suppressing weaker channel connections, thereby obtaining an adaptive adjacency matrix ÃD. This approach enables the model to effectively handle varying emotional patterns and facilitates end-to-end learning.

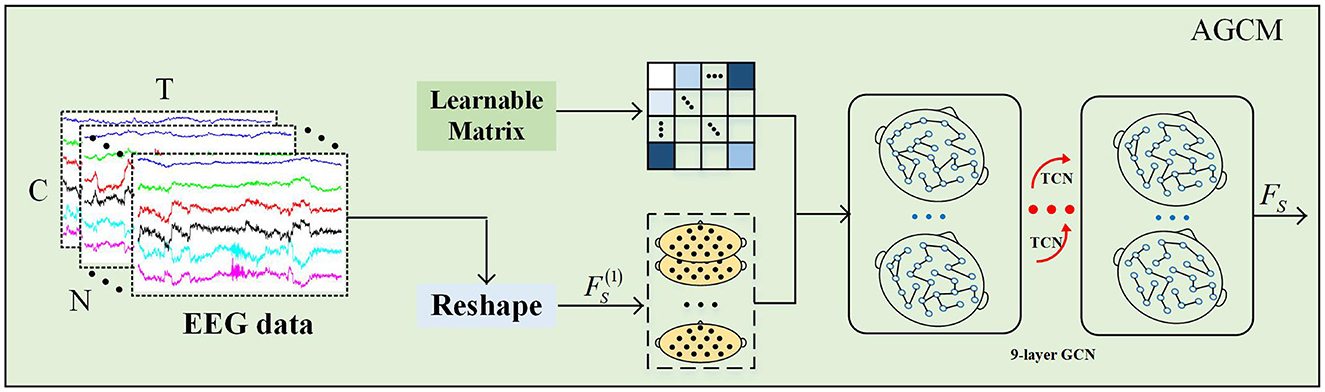
Figure 3. The AGCM.

To fully exploit the temporal information in the data, we incorporated a temporal convolution module and multiple residual connections on top of the dynamic graph convolution. This strategy not only enables the AGCM to capture local dependencies in the temporal dimension but also accurately captures the dynamic evolution characteristics of nodes in the spatial dimension. First, to capture spatial relationships, a transformation operation is applied to convert the preprocessed EEG data input X into FS(1)∈ℝN×1×T×C to obtain the latent spatial features, where 1 denotes the initial feature dimension of AGCM. The update process for each layer of AGCM can be defined as follows:

FS(l)=TCN(σ(ÃDFS(l-1)WG))+FS(l-1),l∈[1,L]    (2)

here, TCN(·) denotes the temporal convolution layer, WG denotes the weights of the graph convolution layer, and FS(l-1) denotes to the spatial features output from the previous layer. In this design, we employ a deep GCN design with L = 6 layers to explore latent dependencies between nodes in the EEG electrode channels, thereby extracting key spatial features FS∈ℝN×T×C.

2.3.2 Temporal self-transformer representation module

Different time points in EEG are interrelated, with each time point contributing differently to the emotion recognition task, making it crucial to analyze temporal features of EEG. To focus on more valuable temporal information, TSRM must effectively capture the global temporal dependencies of the EEG signal, assigning higher scores to the most relevant temporal information through a self-attention-based transformer mechanism.

As shown in Figure 4, TSRM primarily consists of positional encoding, self-attention mechanism, feed-forward layers, and regularization layers. Firstly, we use the preprocessed EEG data X as temporal features and introduce relative positional encoding (PE) to help the model capture the dependencies between different positions in the time series. Let the temporal positions be denoted as pos and the time points as t, the positional encoding is described as follows:

{PE(pos,2t)=sin(pos100002t/d)PE(pos,2t+1)=cos(pos100002t/d)    (3)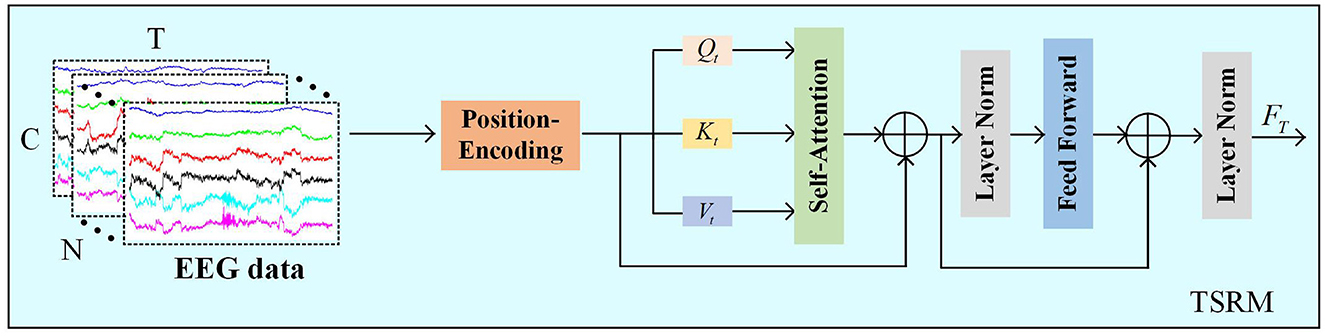

Figure 4. The TSRM.

In this context, d represents the dimension of the temporal vectors. To construct these temporal vectors, we employ sine functions to encode positional information for even time points, while cosine functions are utilized for odd time points.

We then add the positional encoding vectors PE to the feature vectors of the input sequence X to generate the final feature representation:

here, FPE denotes the feature map after relative positional encoding. Then, TSRM obtains the query vectors (Qt), key vectors (Kt), and value vectors (Vt) by multiplying the feature map with three different weight matrices. Subsequently, the dot product is computed between the query vectors Qt and all key vectors Kt, and adjusted by a scaling factor dk.

Next, the Softmax function is applied to normalize the adjusted dot product values, generating a score for each value. The computation process for the typical score matrix across all channels is as follows:

(Qt,Kt,Vt)=((FPEWtQ),(FPEWtK),(FPEWtV))    (5) Attention (Qt,Kt)=Softmax (QtKtTdk)    (6)

here, WtQ∈ℝC×d, WtK∈ℝC×d, WtV∈ℝC×d and denote the parameters of the linear transformations. The shape of the output matrix Attention(Qt, Kt) is [N, T, T].

In the score matrix Attention(Qt, Kt), values across all channels are aggregated with the available information to update the matrix. To mitigate the vanishing gradient problem, residual connections are incorporated. Furthermore, self-attention is integrated with a feed-forward network (FFN) consisting of two fully connected layers followed by a ReLU activation function. The process is delineated as follows:

VT*=Attention(QT,KT)VT    (7) Fres=LN(VT*+FPE)    (8) FT=LN(Fres+FFN(Fres))∈ℝN×T×C    (9)

here, VT*∈N×T×C and Fres∈ℝN×T×C denote the output features from the self-attention mechanism and the FFN, respectively. LN(·) denotes layer normalization, which is incorporated into the TSRM to reduce training time and enhance the model's generalization capability.

2.3.3 Multi-structured transformer fusion module

Through the aforementioned steps, we obtain spatial feature FS and temporal feature FT. Cross-attention-based spatiotemporal feature fusion methods use features from one modality to guide the learning weights of features from another modality. However, this approach does not balance the importance between the two types of features. Traditional simple combination methods (e.g., weighted combination of two cross-attention blocks) may lead to data sparsity and require more computational resources. Therefore, we propose a novel cross-attention mechanism to leverage the complementary information between different modalities, enabling the model to extract more representative features, as illustrated in Figure 5.

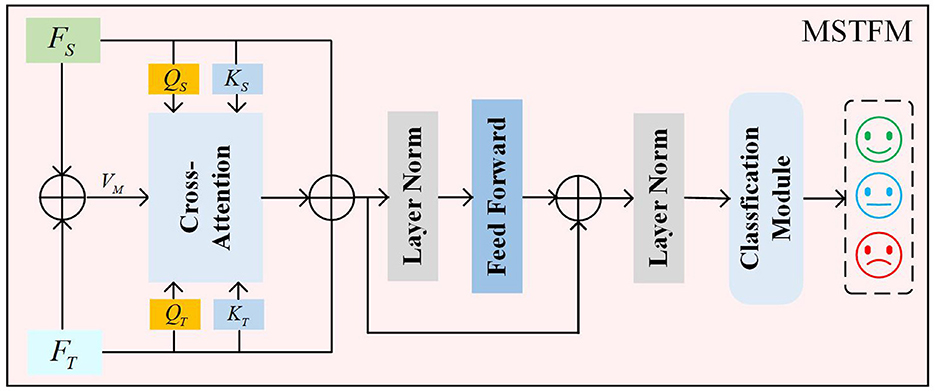
Figure 5. The MSTFM.

First, to fully utilize the correlation and complementarity between different modality features, we introduce intermediate features to mitigate the discrepancies between these features. The intermediate features are obtained by a weighted summation of FS and FT, as detailed in the following formula:

FM=FT⊕FS,FM∈ℝN×T×C    (10)

here, FM denotes the intermediate state features, and ⊕ denotes the weighted summation operation. Through the module's weight learning, the attention weights for both features are guided by the intermediate state features, thereby uncovering shared semantic information between features and emphasizing the differences in their semantic information.

Next, the spatial features FS and temporal features FT are multiplied by different weight matrices to obtain their respective query vectors (QS, QT) and key vectors (KT, KS). Simultaneously, the intermediate state features FM are multiplied by a weight matrix WMV to obtain the value vectors VM. The specific formulas are as follows:

(QS,KS,QT,KT)=((FSWSQ),(FSWSK),(FTWTQ),(FTWTK))    (11)

here, WSQ∈ℝC×d, WSK∈ℝC×d, WTQ∈ℝC×d, WTK∈ℝC×d and WMV∈ℝC×d represent the weight parameters for the linear transformations.

Then, based on the principles of the cross-attention mechanism, the query vectors (QS, QT) and key vectors (KS, KT) obtained from different features are used to compute two typical score matrices, as detailed in the following formulas:

{CAST(QS,KT)=Softmax (QS(KT)Td)CATS(QT,KS)=Softmax (QT(KS)Td)    (13)

here, Softmax(·) denotes the Softmax activation function, and d represents the scaling factor. CAST(QS,KT)∈ℝN×T×T measures the attention score of temporal features from the perspective of spatial features. CATS(QT,KS)∈ℝN×T×T measures the attention score of spatial features from the perspective of temporal features.

Finally, the CAST(QS, KT) and CATS(QT, KS) score matrices are aggregated with the value vectors VM to update the matrices. The proposed cross-attention mechanism integrates these two cross-attention matrices, providing a composite measure of the correlations between temporal and spatial features. The final result is defined as follows:

VM*=CAST(QS,KT)×VM×CATS(QT